数据结构实现 3.1：二分搜索树（C++版）

其他 2018-11-27 03:18:33 阅读次数: 0

数据结构实现 3.1：二分搜索树（C++版）

1. 概念及基本框架

二分搜索树 是一种 半线性结构 ，而且存储上属于 链式存储（即内存的物理空间是不连续的），是树形结构的一种。二分搜索树结构如下图所示：
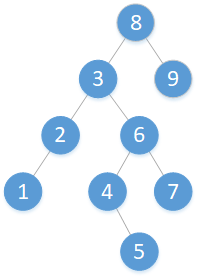
二分搜索树
首先，二分搜索树 作为 二叉树 的一种，有着二叉树的基本特性：
1.每个结点（ 根结点 除外）都有一个 前驱结点（即其父结点）。
2.每个结点至多有两个 后继结点（即其子结点）。
此外，二分搜索树还有一些特殊的特性：
1.每个结点 左孩子 及其后代的值都 小于 这个结点的值。
2.每个结点 右孩子 及其后代的值都 大于 这个结点的值。
3.结点的值 不重复 。
所以，能以二分搜索树结构存放的数据有着一条基本要：可比性 。
下面以一个我实现的一个简单的二分搜索树类来进一步理解二分搜索树。

template <class T>
class BTNode{
public:
	BTNode(T num, BTNode<T> *left = NULL, BTNode<T> *right = NULL){
		m_data = num;
		this->left = left;
		this->right = right;
	}
public:
	T m_data;
	BTNode<T> *left;
	BTNode<T> *right;
};

和链表类似，首先设计一个 结点类 ，这个结点类包含 数据 和 指向左右两边结点的指针 。结点类的构造函数可以直接对结点赋值，然后利用结点类对象来创建一棵二叉搜索树。二叉搜索树类的设计如下：

template <class T>
class BST{
public:
	BST(){
		root = NULL;
	}
	...	
private:
	BTNode<T> *root;
	int m_size;
};

这里为了避免重复设计就可以兼容更多数据类型，引入了 泛型 ，即 模板 的概念。（模板的关键字是 class 或 typename）
这里的 root 表示 根节点 ，m_size 表示 二分搜索树大小 。为了保护数据，这些变量都设置为 private 。
与链表不同的是，二分搜索树一般不需要引入 虚拟头结点 的概念。
实现了前面的程序之后，接下来就是一个二分搜索树的增、删、查以及一些其他基本操作，接下来利用代码去实现。

2. 基本操作程序实现

2.1 增加操作

template <class T>
class BST{
public:
	...
	//增加操作
	void add(T num);
	...
private:
	BTNode<T>* add(BTNode<T> *node, T num);
	...
};

首先，在类体内进行增加操作函数的原型说明。这里包括两个函数：
add (public)
add (private)
这里为什么这么做呢？因为对于树结构来讲，不管是增、删、改、查，还是遍历操作，根节点是一个很重要的结点。为了保护数据，这个结点一般对用户是屏蔽的，即用户不需要知道根节点就可以完成需要的操作。
而对于树结构来说，这些操作一般都是通过递归来实现的（某些操作使用了非递归的方式进行了实现），递归的时候往往需要结点参数，所以这里利用了一个 public 函数来调用另一个 private 函数实现操作，下面的操作也是这样。
注：树的操作也可以使用非递归的方式实现，这里只是为了方便代码编写以及理解，使用了递归的方式。同理，对于链表的操作而言，也可以使用递归的方式进行实现。

template <class T>
void BST<T>::add(T num){
	root = add(root, num);
}
template <class T>
BTNode<T>* BST<T>::add(BTNode<T> *node, T num){
	if (node == NULL){
		m_size++;
		return new BTNode<T>(num);
	}
	else if (num < node->m_data){
		node->left = add(node->left, num);
	}
	else if(num > node->m_data){
		node->right = add(node->right, num);
	}
	return node;
}

由于这些函数在类体外，所以每个函数头部必须添加一行代码：

template <class T>

表示该函数使用模板，下面同理。
注意理解这里私有的 add 函数，为了方便代码编写，特意加了返回值。如果不加返回值，函数是通过父结点连接要添加的子结点，而加了返回值就可以将子结点返回给父结点，操作更加简便。

2.2 删除操作

对于二分搜索树来说，为了保证删除操作完成后的树依旧是一棵二分搜索树，我们需要分三种情况讨论：
（1）欲删除结点左右子树均为空

删除1
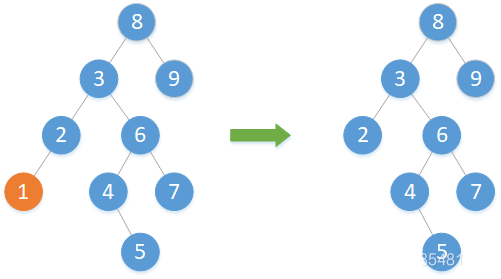
若左右子树均为空，则直接删除该结点，并将其父结点指向删除结点的指针清空。

（2）欲删除结点左右子树仅一方为空

删除2
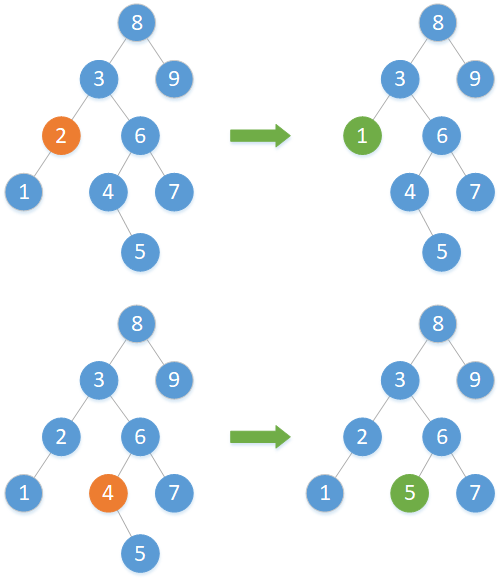
若左右子树仅一方为空，则删除该结点，并将该结点不为空的子树连接到删除结点的父结点指向删除结点的那一支。

（3）欲删除结点左右子树均不为空
删除3
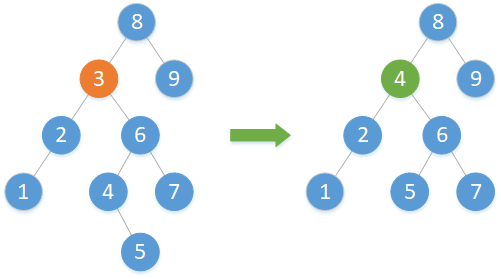
若左右子树均不为空，就用删除结点的右边第一个结点的最左边的结点（即一直往左走，直到该结点的左子树为空的那个结点）来替换掉删除结点，然后删除掉该结点。而用来替换的那个结点的后代也注意需要维护，不能丢失。

template <class T>
class BST{
public:
	...
	//删除操作
	void remove(T num);
	...
private:
	...
	BTNode<T>* remove(BTNode<T> *node, T num);
	...
};

同理，在类体内进行删除函数的原型说明。这里包括两个函数：
remove (public)
remove (private)
分别去实现它们。

template <class T>
void BST<T>::remove(T num){
	root = remove(root, num);
}
template <class T>
BTNode<T>* BST<T>::remove(BTNode<T> *node, T num){
	if (node == NULL){
		return node;
	}
	if (num < node->m_data){
		node->left = remove(node->left, num);
	}
	else if (num > node->m_data){
		node->right = remove(node->right, num);
	}
	else if (num == node->m_data){
		if (node->left == NULL){
			BTNode<T> *rightNode = node->right;
			delete node;
			m_size--;
			return rightNode;
		}
		else if (node->right == NULL){
			BTNode<T> *leftNode = node->left;
			delete node;
			m_size--;
			return leftNode;
		}
		else{
			BTNode<T> *minNode = node->right;
			for (; minNode->left; minNode = minNode->left);
			node->m_data = minNode->m_data;
			node->right = remove(node->right, minNode->m_data);
			return node;
		}
	}
	return node;
}

2.3 查找操作

template <class T>
class BST{
public:
	...
	//查找操作
	bool contains(T num);
	...
private:
	...
	bool contains(BTNode<T> *node, T num);
	...
};

同样，查找操作也有两个函数：
contains (public)
contains (private)

template <class T>
bool BST<T>::contains(T num){
	return contains(root, num);
}
template <class T>
bool BST<T>::contains(BTNode<T> *node, T num){
	if (node == NULL){
		return false;
	}
	if (num == node->m_data){
		return true;
	}
	else if (num < node->m_data){
		return contains(node->left, num);
	}
	else{
		return contains(node->right, num);
	}
}

2.4 遍历操作

树的遍历是一个很重要的概念，下面给出一张图来说明四种遍历的过程。
注：因为二叉树的遍历操作是通用的，所以这里并没有以二分搜索树为例子，而是一棵普通的二叉树。
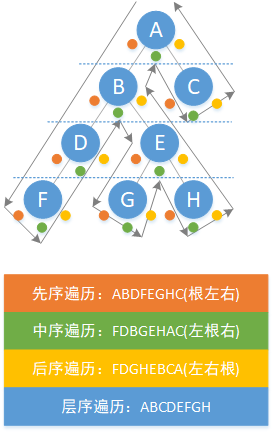
二叉树的遍历
二叉树的先（中或后）序遍历实际上表示的是结点被访问第几次会输出。
先序遍历表示第一次被访问时（橙色）会输出；
中序遍历表示第二次被访问时（绿色）会输出；
后序遍历表示第三次被访问时（黄色）会输出。
这三种遍历的递归版本比较容易实现，依靠输出位置的不同决定是哪一种遍历。这三种遍历实质上是一种 深度优先 遍历。而非递归版本比较难，下面也给出了一种程序实现方法。
注：这三种遍历的非递归版本利用调用栈来实现，这里我们使用了我们在 1.2 中实现的 数组栈 作为调用栈。
层序遍历表示一层一层（图中的蓝色虚线）的访问输出，使用的是非递归的方法，调用了一个队列来实现，层序遍历实质上是一种 广度优先 遍历。
注：层序遍历实现利用了我们在 1.4 中实现的 循环队列 作为调用队列。

template <class T>
class BST{
public:
	...
	//遍历操作
	void preOrder();
	void inOrder();
	void postOrder();
	void preOrderNR();
	void inOrderNR();
	void postOrderNR();
	void levelOrder();
private:
	...
	void preOrder(BTNode<T> *node);
	void inOrder(BTNode<T> *node);
	void postOrder(BTNode<T> *node);
	...
};

这里遍历函数较多，一共有十个：
preOrder (public)：先序遍历
preOrder (private)
preOrder (public)：中序遍历
preOrder (private)
preOrder (public)：后序遍历
preOrder (private)
preOrderNR：先序遍历（非递归版本）
inOrderNR：中序遍历（非递归版本）
postOrderNR：后序遍历（非递归版本）
levelOrder：层序遍历
和前面的函数一样，递归版本的遍历函数有 public 和 private 两个，实现递归版本遍历的操作。然后又实现了三种遍历操作的非递归版本，以及层序遍历（非递归）。下面分别对它们进行实现。

template <class T>
void BST<T>::preOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "先序遍历：";
	preOrder(root);
	cout << endl;
}
template <class T>
void BST<T>::preOrder(BTNode<T> *node){
	if (node == NULL){
		return;
	}
	cout << node->m_data << "  ";
	preOrder(node->left);
	preOrder(node->right);
}
template <class T>
void BST<T>::inOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "中序遍历：";
	inOrder(root);
	cout << endl;
}
template <class T>
void BST<T>::inOrder(BTNode<T> *node){
	if (node == NULL){
		return;
	}
	inOrder(node->left);
	cout << node->m_data << "  ";
	inOrder(node->right);
}
template <class T>
void BST<T>::postOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "后序遍历：";
	postOrder(root);
	cout << endl;
}
template <class T>
void BST<T>::postOrder(BTNode<T> *node){
	if (node == NULL){
		return;
	}
	postOrder(node->left);
	postOrder(node->right);
	cout << node->m_data << "  ";
}
template <class T>
void BST<T>::preOrderNR(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "先序遍历（非递归）：";
	ArrayStack<BTNode<T>*> s;
	s.push(root);
	while (!s.isEmpty()){
		BTNode<T> *node = s.peek();
		cout << node->m_data << "  ";
		s.pop();
		if (node->right != NULL){
			s.push(node->right);
		}
		if (node->left != NULL){
			s.push(node->left);
		}
	}
	cout << endl;
}
template <class T>
void BST<T>::inOrderNR(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "中序遍历（非递归）：";
	ArrayStack<BTNode<T>*> s;
	BTNode<T> *node = root;
	while (node != NULL || !s.isEmpty()){
		while (node != NULL){
			s.push(node);
			node = node->left;
		}
		node = s.peek();
		cout << node->m_data << "  ";
		s.pop();
		if (node->right != NULL){
			node = node->right;  
		}
		else{
			node = NULL;
		}
	}
	cout << endl;
}
template <class T>
void BST<T>::postOrderNR(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "后序遍历（非递归）：";
	ArrayStack<BTNode<T>*> s;
	BTNode<T> *node = root;
	BTNode<T> *lastVisited = root;
	while (node != NULL || !s.isEmpty()){
		while (node != NULL){
			s.push(node);
			node = node->left;
		}
		node = s.peek();
		if (node->right != NULL && lastVisited != node->right){
			node = node->right;
		}
		else{
			lastVisited = node;
			cout << node->m_data << "  ";
			s.pop();
			node = NULL;
		}
	}
	cout << endl;
}
template <class T>
void BST<T>::levelOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "层序遍历：";
	LoopQueue<BTNode<T>*> q;
	q.enqueue(root);
	while (!q.isEmpty()){
		BTNode<T> *node = q.front();
		cout << node->m_data << "  ";
		q.dequeue();
		if (node->left != NULL){
			q.enqueue(node->left);
		}
		if (node->right != NULL){
			q.enqueue(node->right);
		}
	}
	cout << endl;
}

2.5 其他操作

二分搜索树还有一些其他的操作，这些函数我在类体内进行了实现。
包括 二分搜索树大小 的查询等操作。

template <class T>
class BST{
public:
	...
	int size(){
		return m_size;
	}
	bool isEmpty(){
		return root == NULL;
	}
	...
};

3. 算法复杂度分析

3.1 增加操作

函数 最坏复杂度 平均复杂度
add O(n) O(logn)

因为二分搜索树的特有性质，这里平均复杂度是以 2 为底 n 的对数，简单写作 logn ，即其是对数级别的时间复杂度，下面的同理，这正是二分搜索树的优点。

3.2 删除操作

函数 最坏复杂度 平均复杂度
remove O(n) O(logn)

3.3 查找操作

函数 最坏复杂度 平均复杂度
contains O(n) O(logn)

总体情况：

操作 时间复杂度
增 O(logn)
删 O(logn)
查 O(logn)

因为二分搜索树的特有性质，所以操作的复杂度都是 O(logn) 级别的，和线性结构相比，（线性结构很多操作需要 O(n) 级别的时间复杂度）充分体现出二分搜索树这一结构的优点。

4. 完整代码

程序完整代码（这里使用了头文件的形式来实现类）如下：
其中，数组栈 类以及 循环队列 类的代码不再重复给出，如有需要，可以查看 1.2 和 1.4的内容。

#ifndef __BST_H__
#define __BST_H__

#include "ArrayStack.h"
#include "LoopQueue.h"

template <class T>
class BTNode{
public:
	BTNode(T num, BTNode<T> *left = NULL, BTNode<T> *right = NULL){
		m_data = num;
		this->left = left;
		this->right = right;
	}
public:
	T m_data;
	BTNode<T> *left;
	BTNode<T> *right;
};
template <class T>
class BST{
public:
	BST(){
		root = NULL;
	}
	int size(){
		return m_size;
	}
	bool isEmpty(){
		return root == NULL;
	}
	//增加操作
	void add(T num);
	//删除操作
	void remove(T num);
	//查找操作
	bool contains(T num);
	//遍历操作
	void preOrder();
	void inOrder();
	void postOrder();
	void preOrderNR();
	void inOrderNR();
	void postOrderNR();
	void levelOrder();
private:
	BTNode<T>* add(BTNode<T> *node, T num);
	BTNode<T>* remove(BTNode<T> *node, T num);
	bool contains(BTNode<T> *node, T num);
	void preOrder(BTNode<T> *node);
	void inOrder(BTNode<T> *node);
	void postOrder(BTNode<T> *node);
private:
	BTNode<T> *root;
	int m_size;
};

template <class T>
void BST<T>::add(T num){
	root = add(root, num);
}
template <class T>
BTNode<T>* BST<T>::add(BTNode<T> *node, T num){
	if (node == NULL){
		m_size++;
		return new BTNode<T>(num);
	}
	else if (num < node->m_data){
		node->left = add(node->left, num);
	}
	else if(num > node->m_data){
		node->right = add(node->right, num);
	}
	return node;
}

template <class T>
void BST<T>::remove(T num){
	root = remove(root, num);
}
template <class T>
BTNode<T>* BST<T>::remove(BTNode<T> *node, T num){
	if (node == NULL){
		return node;
	}
	if (num < node->m_data){
		node->left = remove(node->left, num);
	}
	else if (num > node->m_data){
		node->right = remove(node->right, num);
	}
	else if (num == node->m_data){
		if (node->left == NULL){
			BTNode<T> *rightNode = node->right;
			delete node;
			m_size--;
			return rightNode;
		}
		else if (node->right == NULL){
			BTNode<T> *leftNode = node->left;
			delete node;
			m_size--;
			return leftNode;
		}
		else{
			BTNode<T> *minNode = node->right;
			for (; minNode->left; minNode = minNode->left);
			node->m_data = minNode->m_data;
			node->right = remove(node->right, minNode->m_data);
			return node;
		}
	}
	return node;
}

template <class T>
bool BST<T>::contains(T num){
	return contains(root, num);
}
template <class T>
bool BST<T>::contains(BTNode<T> *node, T num){
	if (node == NULL){
		return false;
	}
	if (num == node->m_data){
		return true;
	}
	else if (num < node->m_data){
		return contains(node->left, num);
	}
	else{
		return contains(node->right, num);
	}
}

template <class T>
void BST<T>::preOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "先序遍历：";
	preOrder(root);
	cout << endl;
}
template <class T>
void BST<T>::preOrder(BTNode<T> *node){
	if (node == NULL){
		return;
	}
	cout << node->m_data << "  ";
	preOrder(node->left);
	preOrder(node->right);
}
template <class T>
void BST<T>::inOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "中序遍历：";
	inOrder(root);
	cout << endl;
}
template <class T>
void BST<T>::inOrder(BTNode<T> *node){
	if (node == NULL){
		return;
	}
	inOrder(node->left);
	cout << node->m_data << "  ";
	inOrder(node->right);
}
template <class T>
void BST<T>::postOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "后序遍历：";
	postOrder(root);
	cout << endl;
}
template <class T>
void BST<T>::postOrder(BTNode<T> *node){
	if (node == NULL){
		return;
	}
	postOrder(node->left);
	postOrder(node->right);
	cout << node->m_data << "  ";
}
template <class T>
void BST<T>::preOrderNR(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "先序遍历（非递归）：";
	ArrayStack<BTNode<T>*> s;
	s.push(root);
	while (!s.isEmpty()){
		BTNode<T> *node = s.peek();
		cout << node->m_data << "  ";
		s.pop();
		if (node->right != NULL){
			s.push(node->right);
		}
		if (node->left != NULL){
			s.push(node->left);
		}
	}
	cout << endl;
}
template <class T>
void BST<T>::inOrderNR(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "中序遍历（非递归）：";
	ArrayStack<BTNode<T>*> s;
	BTNode<T> *node = root;
	while (node != NULL || !s.isEmpty()){
		while (node != NULL){
			s.push(node);
			node = node->left;
		}
		node = s.peek();
		cout << node->m_data << "  ";
		s.pop();
		if (node->right != NULL){
			node = node->right;  
		}
		else{
			node = NULL;
		}
	}
	cout << endl;
}
template <class T>
void BST<T>::postOrderNR(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "后序遍历（非递归）：";
	ArrayStack<BTNode<T>*> s;
	BTNode<T> *node = root;
	BTNode<T> *lastVisited = root;
	while (node != NULL || !s.isEmpty()){
		while (node != NULL){
			s.push(node);
			node = node->left;
		}
		node = s.peek();
		if (node->right != NULL && lastVisited != node->right){
			node = node->right;
		}
		else{
			lastVisited = node;
			cout << node->m_data << "  ";
			s.pop();
			node = NULL;
		}
	}
	cout << endl;
}
template <class T>
void BST<T>::levelOrder(){
	cout << "Binary Search Tree: " << "Size = " << m_size << endl;
	cout << "层序遍历：";
	LoopQueue<BTNode<T>*> q;
	q.enqueue(root);
	while (!q.isEmpty()){
		BTNode<T> *node = q.front();
		cout << node->m_data << "  ";
		q.dequeue();
		if (node->left != NULL){
			q.enqueue(node->left);
		}
		if (node->right != NULL){
			q.enqueue(node->right);
		}
	}
	cout << endl;
}

#endif

猜你喜欢

转载自blog.csdn.net/qq_35481167/article/details/83994855
今日推荐
基于大语言模型的开源知识库问答系统 MaxKB GitHub Star 数量突破 5,000 个！
美国拟限制 AI 大模型出口中国和俄罗斯
苹果将与 OpenAI 达成协议，将 ChatGPT 应用于 iPhone
openKylin 社区生态委员会第六次会议圆满召开
阿里云正式发布通义千问 2.5
Python 3.13 发布首个 Beta：实验性自由线程模式和 JIT、改进交互式解释器
Stack Overflow 拿我的代码去训练 AI 大模型，还封了我的账号
Pop!_OS 的 COSMIC 桌面完成 App Store 上架工作
报告：Django 仍然是 74% 开发者的首选
《2024 年一季度互联网投融资运行情况》研究报告
15 年前上了“FFmpeg 耻辱柱”，今天他还得谢谢咱——腾讯QQPlayer一雪前耻？
TIOBE 5 月榜单：Fortran “复活”进入 Top 10
周排行
BPM为企业带来的实际利益
好程序员web前端分享css常用属性缩写
Java文件下载（excel）
css样式的动态添加及显示和隐藏等零碎用法
axios全局配置以及拦截器
使用Logstash来实时同步MySQL和log日志数据到ES
C++获取当前时间（年月日、时分秒、毫秒）
Odoo产品分析 (四) -- 工具板块(11) -- 网站即时聊天(1)
Java环境配置正确，但是java、javac、java -version均返回“不是内部或外部命令，也不是可运行的程序或批处理文件”？
01 官网下载各种CentOS教程（超详细版）
每日归档
更多
2024-05-14(0)
2024-05-13(18)
2024-05-12(0)
2024-05-11(38)
2024-05-10(38)
2024-05-09(35)
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022