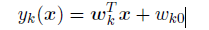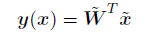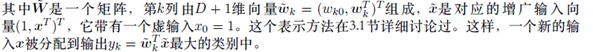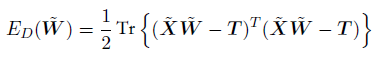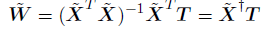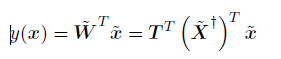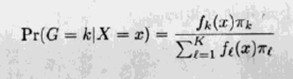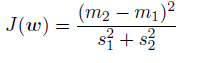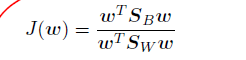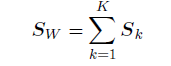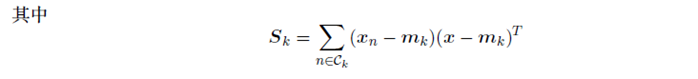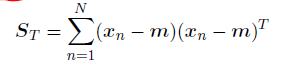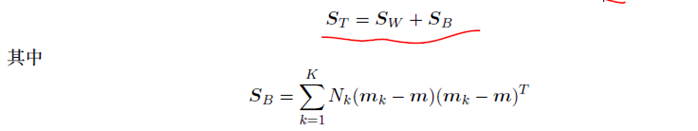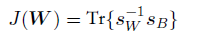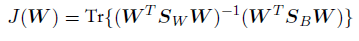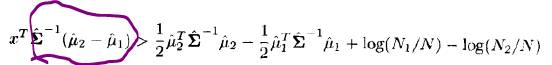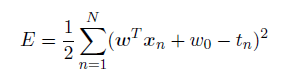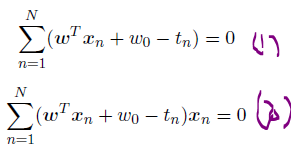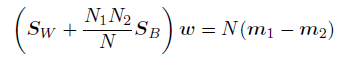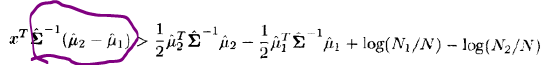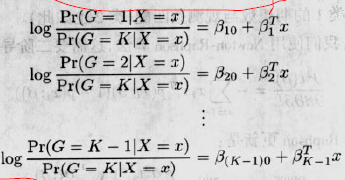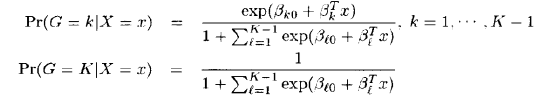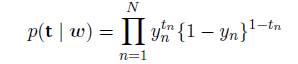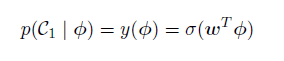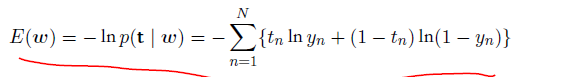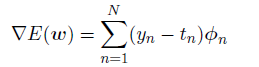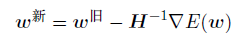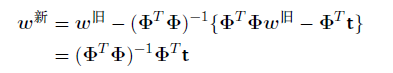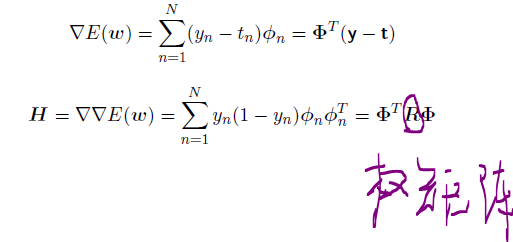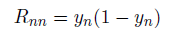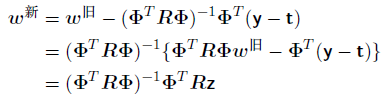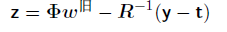分类的线性方法(PRML 4.*、ESL 4.*)
在本章中,我们考虑分类的线性模型。所谓分类线性模型,是指决策⾯是输⼊向量x的线性函数,因此被定义为D维输⼊空间中的(D-1)维超平⾯。
Prml\esl中的线性分类模型涉及到
指示矩阵线性回归模型
线性判别分析(LDA)
Logistic回归
分离超平面
指示矩阵的线性回归模型
方法:
用线性回归模型拟合类指示变量,并分类到最大拟合(esl定义)
指示变量编码:
如果类别有K个,用1-of-K编码方式
例如每一个xn的响应(类别)变量表示为tn = (0,0,0,…,0,1,0)
每个类别Ck由⾃⼰的线性模型描述,即
其中k = 1; : : : ;K。使⽤向量记号,我们可以很容易地把这些量聚集在⼀起表⽰,即
我们现在通过最⼩化平⽅和误差函数来确定参数矩阵~W
,
令上式关于~W的导数等于零,整理,可以得到~W的解,形式为
其中~X^十字是矩阵~X的伪逆矩阵,正如3.1.1节讨论的那样。这样我们得到了判别函数,形式为
但是这个模型有一些问题:
最⼩平⽅解对于离群点缺少鲁棒性, 平⽅和误差函数惩罚了"过于正确"的预测.
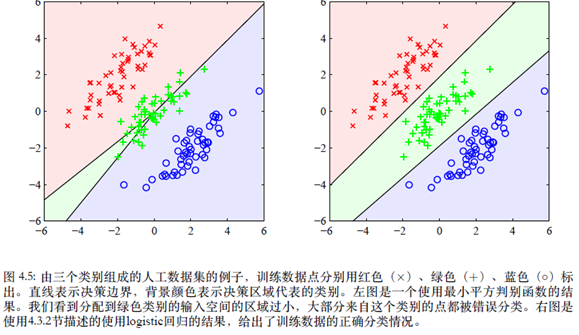
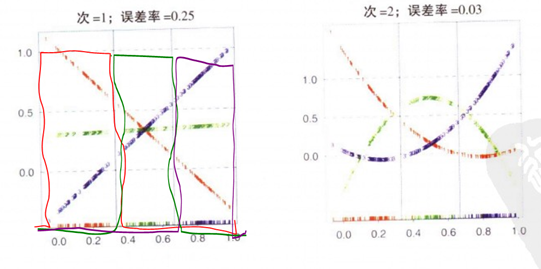
但是,最⼩平⽅⽅法的问题实际上⽐简单的缺乏鲁棒性更加严重,如图4.5所⽰。这幅图给出了⼆维空间(x1; x2)中,来⾃三个类别的⼈⼯⽣成的数据。线性决策边界能够将数据点完美地分开。实际上,在本章的后⾯将要介绍的逻辑回归⽅法可以给出⼀个令⼈满意的解,如右侧的图所⽰。然⽽,最⼩平⽅⽅法给出的结果相当差,输⼊空间中只有⼀个相当⼩的区域被分给了绿⾊的类别。
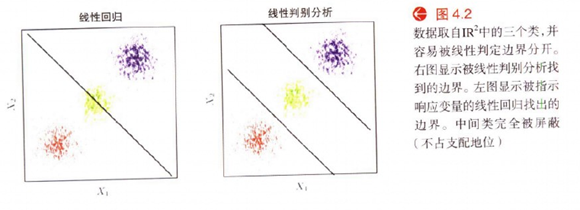
由上图左边图可以看出,线性回归模型试图拟合阶梯型0-1函数,又因为每一类的得分之和必须为1,因此拟合结果为上图左边.这就使得在图4.2左边处于中间位置的数据团(当其数量不是很多时)拟合的直线(图4.3左中的绿色直线)位置偏下(数据量少,概率低),因此"不占支配地位,被屏蔽."(esl)
(上图中的阶梯型函数就是线性回归模型需要拟合的目标曲线).
最⼩平⽅⽅法的失败并不让我们感觉惊讶。回忆⼀下,最⼩平⽅⽅法对应于⾼斯条件分布假设下的最⼤似然法,⽽⼆值⽬标向量的概率分布显然不是⾼斯分布。通过使⽤更恰当的概率模型,我们会得到性质⽐最⼩平⽅⽅法更好的分类⽅法。
线性判别分析
模型定义
由分类的判定理论(esl2.4)可知, 为了最优分类, 我们需要知道后验概率P(G|X). 设f_k(x)是类G=k中X的类条件密度,而pi_x是类k的先验, 并且sum_k(pi_k) = 1.贝叶斯定理的简单应用给出:
我们看到,从分类能力将,有了f_k(x)几乎等价于有了P(G=k|X=x).
许多技术都是基于类密度的模型:
有上面可以看出,LDA是基于高斯,其次假设每一类的协方差矩阵相同.
LDA与QDA
二次判别式则去掉协方差相同的假设,因此上述的判别函数含有二次项.
LDA与QDA的比较着重考虑参数多少(LDA参数少,QDA参数较多)
LDA的计算
降秩线性判别分析(Fisher线性判别函数)
迄今为止,LDA作为一种受限的高斯分类法,他的流行部分因为附加的限制允许我们观察数据的富含信息的低维投影.
P维输入的k个形心在一个小于等于K-1维的仿射子空间中.如果p很大,则可以相当可观的降维.此外,为了去顶最近的形心,我们可以忽略正交于子空间的距离.这样,便可以把X^*投影到这个形心生成的子空间中H_(k-1),并在那里做距离比较.
这样,LDA存在一个基本的维归约,即最多需要在K-1维子空间上考虑数据.
K-1维只是k个类分开的子空间维度的上限.即K个类最多存在于一个K-1维空间中.K个类也可能存在于一维直线上.
如果K>3会怎样?我们可以寻找某个L<=K-1子空间H_L,使得它在某种意义下(loss)对LDA是最佳的.
Fisher定义最佳的含义是投影后的形心在方差意义下尽可能分散.
实际上,Fisher准则根据类间方差与类内方差的比值定义:
我们可以使⽤公式(4.20)、公式(4.23)和公式(4.24)对这个式⼦重写,显式地表达出J(w)对w的依赖。
对公式J(W)关于w求导,我们发现J(w)取得最⼤值的条件为
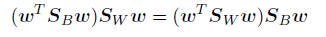
根据公式S_B,我们看到S_B*w总是在(m2 -m1)的⽅向上。更重要的是,我们不关⼼w的⼤⼩,只关⼼它的⽅向,因此我们可以忽略标量因⼦(wTSBw)和(wTSWw)。将公式(4.29)的两侧乘以S_w^-1,我们有
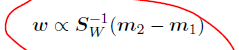
注意,如果类内协⽅差矩阵是各向同性的,从⽽SW正⽐于单位矩阵,那么我们看到w正⽐于类均值的差。公式(4.30)的结果被称为Fisher线性判别函数(Fisher linear discriminant),虽然严格来说它并不是⼀个判别函数,⽽是对于数据向⼀维投影的⽅向的⼀个具体选择。
对于多类:
类内协⽅差矩阵可以使⽤公式
其中Nk是类别Ck中模式的数量。为了找到类间协⽅差矩阵的推⼴, 我们使⽤Duda and Hart(1973)的⽅法,⾸先考虑整体的协⽅差矩阵
整体的协⽅差矩阵可以分解为公式(4.40)和公式(4.41)给出的类内协⽅差矩阵,加上另⼀个矩阵SB,它可以看做类间协⽅差矩阵。

与之前⼀样,我们想构造⼀个标量,当类间协⽅差较⼤且类内协⽅差较⼩时,这个标量会较⼤。有许多可能的准则选择⽅式(Fukunaga, 1990)。其中⼀种选择是:
这个判别准则可以显式地写成投影矩阵W的函数,形式为
最⼤化这个判别准则是很直接的,虽然有些⿇烦。详细的推导可以参考Fukunaga(1990)。权值由SW^-1 SB的特征向量确定,它对应了D′个最⼤的特征值。再从数学上看下为什么只有K-1维子空间必需.值得强调的时,有⼀个重要的结果对于所有的这些判别准则都成⽴。⾸先,根据公式SB,SB由K个矩阵的和组成,每⼀个矩阵都是两个向量的外积,因此秩等于1。此外,由于公式(4.44)给出的限制条件,这些矩阵中只有(K - 1)个是相互独⽴的。因此SB的秩最⼤等于(K - 1),因此最多有(K - 1)个⾮零特征值。这表明,向由SB张成的(K - 1)维空间上的投影不会改变J(W)的值,因此通过这种⽅法我们不能够找到多于(K - 1)个线性"特征"(Fukunaga,1990)。
LDA与指示矩阵的线性回归
容易证明:最小二乘方的系数向量正比于下式表示的LDA方向.
下面证明.
⽬前为⽌,我们已经考虑了⽬标变量的"1-of-K"表⽰⽅法来建模指示矩阵的线性回归模型. 然⽽,如果我们使⽤⼀种稍微不同的表达⽅法,那么权值的最⼩平⽅解就会变得等价于Fisher解(Duda and Hart, 1973)特别地,我们让属于C1的⽬标值等于N/N11 ,其中N1是类别C1的模式的数量,N是总的模式数量。这个⽬标值近似于类别C1的先验概率的导数。对于类别C2,我们令⽬标值等于-N/N2,其中N2是类别C2的模式的数量。
平⽅和误差函数可以写成
令E关于w0和w的导数等于零,我们有
根据上(1)公式,使⽤我们对于⽬标值tn的表⽰⽅法,我们可以得到偏置的表达式
通过⼀些简单的计算,并且再次使⽤我们对于tn的新的表⽰⽅法,⽅程(2)变为
我们注意到SBw总是在(m2 -m1)的⽅向上,因此
其中,我们已经忽略了不相关的标量因⼦.因此权向量恰好与LDA准则得到的结果相同.
但是不同的是,LDA还有一个截距,参见公式
当N1不等于N2时,最小二乘法得到的投影方向虽然与LDA得到的投影方向相同,但是LDA还有一个截距,这使得分类策略不同.
Logistic回归
模型定义
逻辑斯缔回归源于这样一种愿望:通过x的线性函数对K个类的后验概率(的对数几率)建模,而同时确保它们的和为1.并且都在[0,1]中.该模型具有如下形式:
该模型用K-1个对数几率或分对数变换确定.尽管模型使用最后一个类作为几率中的分母,但分母的选择是任意的.
简单的计算下得到:
而它们的和显然为1.
由贝叶斯分类理论可知,选择分类器
上述模型属于概率判别式模型.
参数估计
逻辑斯缔回归模型的参数是线性函数的系数.因为分类器定义为最大后验概率,(而且是真正的概率),对响应(目标变量)的编码采用1-of-K方式.tn = [0,0,…1,0]
Loss函数采用负对数似然.
实际上,最大似然估计跟最小化负对数似然Loss本质上是一致的.
首先考虑二分类
对于⼀个数据集ϕn; tn,似然函数可以写成
其中t = (t1; : : : ; tN)T 且yn = p(C1 | ϕn)。
与之前⼀样,我们可以通过取似然函数的负对数的⽅式,定义⼀个误差函数。这种⽅式产⽣了交叉熵(cross-entropy)误差函数
其中yn = sigmoid(an)且an = wTϕn。两侧关于w取误差函数的梯度,我们有
我们看到,涉及到logistic sigmoid的导数的因⼦已经被消去,使得对数似然函数的梯度的形式⼗分简单。特别地,数据点n对梯度的贡献为⽬标值和模型预测值之间的"误差"yn - tn与基函数向量ϕn相乘。此外,与公式(3.13)的对⽐表明,它的函数形式与线性回归模型中的平⽅和误差函数的梯度的函数形式完全相同。
在第3章讨论线性回归模型的时候,在⾼斯噪声模型的假设的情况下,最⼤似然解有解析解。这是因为对数似然函数为参数向量w的⼆次函数。对于logistic回归来说,不再有解析解了,因为logistic sigmoid函数是⼀个⾮线性函数。然⽽,函数形式不是⼆次函数并不是本质的原因。精确地说,正如我们将要看到的那样,误差函数是凸函数,因此有⼀个唯⼀的最⼩值。此外,误差函数可以通过⼀种⾼效的迭代⽅法求出最⼩值,这种迭代⽅法基于Newton-Raphson迭代最优化框架,使⽤了对数似然函数的局部⼆次近似。为了最⼩化函数E(w),Newton-Raphson对权值的更新的形式为(Fletcher, 1987; Bishop and Nabney, 2008)
其中H是⼀个Hessian矩阵,它的元素由E(w)关于w的⼆阶导数组成。
⾸先,让我们把Newton-Raphson⽅法应⽤到纯线性回归模型(3.3)上,误差函数为平⽅和误差函数(3.12)。这个误差函数的梯度和Hessian矩阵为
其中_是N _M设计矩阵,第n⾏为ϕn^T 。于是,Newton-Raphson更新的形式为
我们看到这是标准的最⼩平⽅解。注意, 这种情况下误差函数是⼆次的, 因此Newton-Raphson公式⽤1步就给出了精确解。现在让我们把Newton-Raphson更新应⽤到logistic回归模型的交叉熵误差函数(4.90)上。根据公式(4.91),我们看到这个误差函数的梯度和Hessian矩阵为
推导过程中我们使⽤了公式(4.88)。并且,我们引⼊了⼀个N _ N的对⾓矩阵R,元素为
我们看到Hessian矩阵不再是常量,⽽是通过权矩阵R依赖于w。这对应于误差函数不是⼆次函数的事实。使⽤性质0 < yn < 1(这个性质来⾃于logistic sigmoid函数形式),我们看到对于任意向量u都有uTHu > 0,因此Hessian矩阵H是正定的。因此误差函数是w的⼀个凸函数,从⽽有唯⼀的最⼩值。
这样,logistic回归模型的Newton-Raphson更新公式就变成了
其中z是⼀个N维向量,元素为
我们看到更新公式(4.99)的形式为⼀组加权最⼩平⽅问题的规范⽅程。由于权矩阵R不是常量,⽽是依赖于参数向量w,因此我们必须迭代地应⽤规范⽅程,每次使⽤新的权向量w计算⼀个修正的权矩阵R。由于这个原因,这个算法被称为迭代重加权最⼩平⽅(iterativereweighted least squares),或者简称为IRLS(Rubin, 1983)。与加权的最⼩平⽅问题⼀样,对⾓矩阵R可以看成⽅差,因为logistic回归模型的t的均值和⽅差为
多类逻辑斯缔回归
见PRML 4.34
对线性可分的奇异性
值得注意的⼀点是,最⼤似然⽅法对于线性可分的数据集会产⽣严重的过拟合现象。这是由于最⼤似然解出现在超平⾯对应于_ = 0:5的情况,它等价于wTϕ = 0。最⼤似然解把数据集分成了两类,并且w的⼤⼩趋向于⽆穷⼤。这种情况下,logistic sigmoid函数在特征空间中变得⾮常陡峭,对应于⼀个跳变的阶梯函数,使得每⼀个来⾃类别k的训练数据都被赋予⼀个后验概率p(Ck | x) = 1。此外,通常这些解之间存在连续性,因为任何切分超平⾯都会造成训练数据点中同样的后验概率,正如后⾯在图10.13中将会看到的那样。最⼤似然⽅法⽆法区分某个解优于另⼀个解,并且在实际应⽤中哪个解被找到将会依赖于优化算法的选择和参数的初始化。注意,即使与模型的参数相⽐数据点的数量很多,只要数据是线性可分的,这个问题就会出现。通过引⼊先验概率,然后寻找w的MAP解,或者等价地,通过给误差函数增加⼀个正则化项,这种奇异性就可以被避免。
参数数量
对比概率生成式模型,逻辑斯缔回归模型的参数相对较少.
对于⼀个M维特征空间ϕ,这个模型有M个可调节参数。相反,如果我们使⽤最⼤似然⽅法调节了⾼斯类条件概率密度(生成式模型),那么我们有2M个参数来描述均值,以及M(M+1)/2 个参数来描述(共享的)协⽅差矩阵。算上类先验p(C1),参数的总数为M(M+5)/2 + 1,这随着M的增长⽽以⼆次的⽅式增长。这和logistic回归⽅法中对于参数数量M的线性依赖不同。对于⼤的M值,直接使⽤logistic回归模型有着很明显的优势。
回归系数选择
见ESL 4.42例:南非心脏病