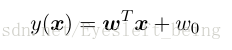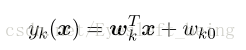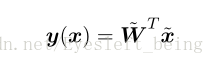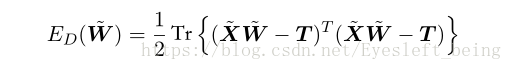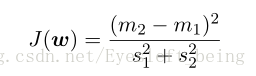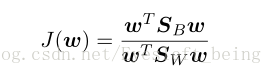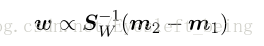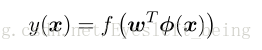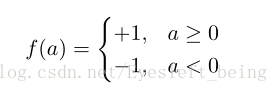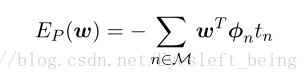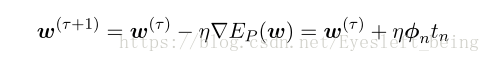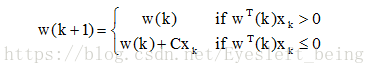数学模型
分类的目标是把输入 x 匹配到唯一的离散型类别 Ck 中。在一个平面中,我们可以用一条直线分开两组数据,所以这条直线,一般来讲是在D维输入空间中的(D-1)维超平面,叫做线性判别函数(Linear discriminant function),也叫决策面(decision surface)
这里的线性,是一种真正意义上的线性,就是函数模型对输入变量x表现出线性(直线、平面、超平面)
1、二分类
代入x, 如果y>0 则输入C1类,y<0 则输入C2类
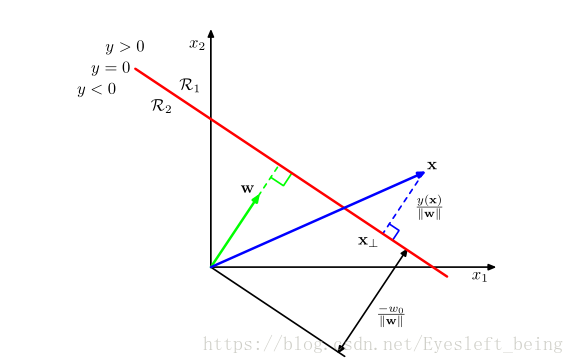
w 表示决策面的方向(w向量垂直于决策面) W0 表示决策面的位置
2、多分类
多分类来自二分类的推广,有K类我们就要引入K个线性判定函数的组合,对于多分类问题的输出t,我们往往用 t=[0 0 0 1 0 0]来表示。
也就是说,x 对应的哪个判定函数最大,那么久输入哪一类!
当然,我们可以把w0包括进去写成下列形式:
线性分类
1、 用于分类的最小平方方法
我们如果想得到分类的模型,然来对进来的数据自动进行分类。这里还可以看做是一个曲线拟合的问题:已知的一些数据,且知道它们的类别,然后让这些因素来估计W的解析解,就用的是最小平方法,这个过程就叫learning
上式中X,T为数据和分类结果,XW是模型值。对w求导数可以得到一个解析解
最小平方方法并不是一个比较好的方法,有一个很大的问题是,对于一些特别点(干扰点)鲁棒性较差,得到不好的效果。实际上,最小平方法的失败并不让我们意外,因为一个严重的问题是,最小平方法是对应于假设高斯分布下的最大似然方法,可是二值目标向量t明显不是高斯分布!
2、 Fisher线性判别
Fisher线性判别的思想是,把高维的数据 x 全部投影到一维的一条直线上!
对于高维空间的数据,它们可能分的很开,但是投影到一条直线上的话,就会造成拥挤甚至覆盖,给分类造成困难。但是我们总能找到一个方向的直线,能让投影下来的点分的最开:同类的点聚集度最高,不同类的点的均值距离最大!
fisher线性判别,核心问题就是要找到这样一条直线。方式就是构造一个fisher准则函数,这个函数的分子是投影后类间的离散度,分母是投影后类中的离散度,这样就转换为了一个球fisher准则函数最大值的问题。
具体过程如下:
用这个公式让 x 投影到一维空间y中,y 表示一个数值。
这就是fisher准则函数。对于二分类的情况,m1 m2是投影后的类均值,s 为投影后的类内的协方差(离散度)
更一般的,我们可以用下式来表示:
这显然是代入了y=wx之后的结果,因为我们要求的就是w,所以必须要建立显式的显示w的fisher准则函数。
其中,SB为类间协方差矩阵,SW为类内协方差矩阵。
这个时候,通过求解这个函数的最大值,我们就可以得到W的方向,如下:
到这里我们可以看出,fisher线性判别法就是一个寻找最优的投影方向的方法,本质上并不是分类。但是,由于变换后的模式是一样的,因此判别界面实际上是各类样本所在轴上的一个点,即确定一个阈值 y0 ,当 wx>=y0时,属于C1类,否则属于C2类。
3、感知器算法
感知器算法是一个二分类的算法,在这个模型中,输入向量 x 先经过固定的非线性变换为一个特征向量ϕ(x),这个特征向量然后被用于构建一个更一般的线性模型
其中感知器f 的性质如下:
我们可以发现,这样就又把分类问题转变成了一个求解权重w的过程。对于分类正确的情况, w T ϕ(x n )t n > 0 即a*f(a)>0 而对于分类错误的情况,结果小于0;
因此,我们把所有的分类错误的情况相加,可以得到一个函数叫感知器准则函数:
求解E的最小值,分类问题转变成一个求极值问题。这里我们不能直接求w的导数等于0,因为好像不能这样做(具体不清楚),所以要用梯度下降法来一次次的更新W
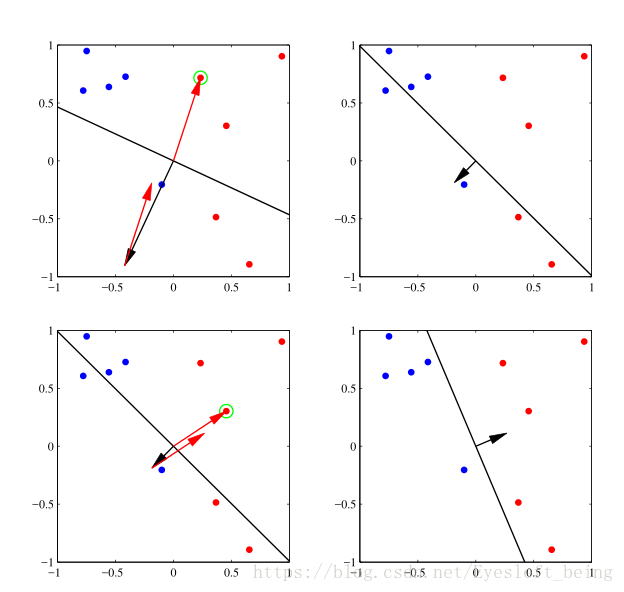
这里的学习率往往设置为1,可以得到下面图所示的过程。
感知器算法无法直接推广到K>2的情形,且对于不能够线性分开的数据算法永远不会收敛。即使是对于线性可分的点,也有可能有多个解,且最终的解依赖于初始值的设定和数据出现的顺序。