版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/winycg/article/details/83043663
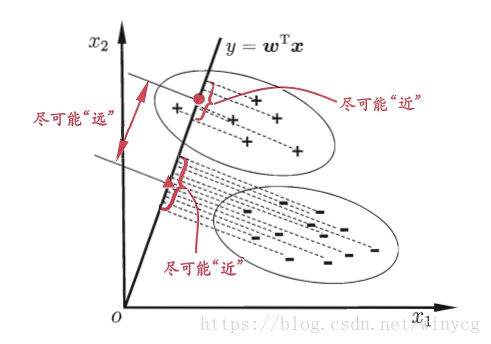
LDA(Linear Discriminant Analysis)是一种经典的线性判别方法,又称Fisher判别分析。该方法思想比较简单:给定训练集样例,设法将样例投影到一维的直线上,使得同类样例的投影点尽可能接近和密集(即希望类内离散度越小越好),异类投影点尽可能远离(即希望两类的均值点之差越小越好)
两类数据点的类心分别是
μ
1
=
1
∣
C
1
∣
∑
x
∈
C
1
x
和
μ
2
=
1
∣
C
2
∣
∑
x
∈
C
2
x
\mu_{1}=\frac{1}{|C_{1}|}\sum_{x\in C_{1}}x和\mu_{2}=\frac{1}{|C_{2}|}\sum_{x\in C_{2}}x
μ 1 = ∣ C 1 ∣ 1 x ∈ C 1 ∑ x 和 μ 2 = ∣ C 2 ∣ 1 x ∈ C 2 ∑ x
x
x
x
w
w
w
y
=
w
T
x
y=w^{T}x
y = w T x
m
k
=
1
∣
C
k
∣
∑
x
∈
C
k
w
T
x
=
w
T
1
∣
C
k
∣
∑
x
∈
C
k
x
=
w
T
μ
k
m_{k}=\frac{1}{|C_{k}|}\sum_{x\in C_{k}}w^{T}x=w^{T}\frac{1}{|C_{k}|}\sum_{x\in C_{k}}x=w^{T}\mu_{k}
m k = ∣ C k ∣ 1 x ∈ C k ∑ w T x = w T ∣ C k ∣ 1 x ∈ C k ∑ x = w T μ k
(
m
1
−
m
2
)
2
=
(
m
1
−
m
2
)
(
m
1
−
m
2
)
T
=
w
T
(
μ
1
−
μ
2
)
(
μ
1
−
μ
2
)
T
w
=
w
T
S
b
w
(m_{1}-m_{2})^{2}=(m_{1}-m_{2})(m_{1}-m_{2})^{T}\\ =w^{T}(\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^{T}w=w^{T}S_{b}w\\
( m 1 − m 2 ) 2 = ( m 1 − m 2 ) ( m 1 − m 2 ) T = w T ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T w = w T S b w
S
b
S_{b}
S b
S
b
=
(
μ
1
−
μ
2
)
(
μ
1
−
μ
2
)
T
S_{b}=(\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^{T}
S b = ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T
k
k
k
S
k
=
∑
x
∈
C
k
(
y
−
m
k
)
2
=
∑
x
∈
C
k
(
w
T
(
x
−
μ
k
)
)
2
=
∑
x
∈
C
k
(
w
T
(
x
−
μ
k
)
)
(
w
T
(
x
−
μ
k
)
)
T
=
∑
x
∈
C
k
(
w
T
(
x
−
μ
k
)
(
x
−
μ
k
)
T
w
)
=
w
T
[
∑
x
∈
C
k
(
x
−
μ
k
)
(
x
−
μ
k
)
T
]
w
S_{k}=\sum_{x\in C_{k}}(y-m_{k})^{2}=\sum_{x\in C_{k}}(w^T({x}-\mu_{k}))^{2}\\ =\sum_{x\in C_{k}}(w^T({x}-\mu_{k}))(w^T({x}-\mu_{k}))^{T}\\ =\sum_{x\in C_{k}}(w^T({x}-\mu_{k})(x-\mu_{k})^{T}w)\\ =w^T[\sum_{x\in C_{k}}({x}-\mu_{k})(x-\mu_{k})^{T}]w
S k = x ∈ C k ∑ ( y − m k ) 2 = x ∈ C k ∑ ( w T ( x − μ k ) ) 2 = x ∈ C k ∑ ( w T ( x − μ k ) ) ( w T ( x − μ k ) ) T = x ∈ C k ∑ ( w T ( x − μ k ) ( x − μ k ) T w ) = w T [ x ∈ C k ∑ ( x − μ k ) ( x − μ k ) T ] w
S
1
2
+
S
2
2
=
w
T
[
∑
x
∈
C
1
(
x
−
μ
1
)
(
x
−
μ
1
)
T
+
∑
x
∈
C
2
(
x
−
μ
2
)
(
x
−
μ
2
)
T
]
w
S_{1}^{2}+S_{2}^{2}\\=w^T[\sum_{x\in C_{1}}({x}-\mu_{1})(x-\mu_{1})^{T}+\sum_{x\in C_{2}}({x}-\mu_{2})(x-\mu_{2})^{T}]w
S 1 2 + S 2 2 = w T [ x ∈ C 1 ∑ ( x − μ 1 ) ( x − μ 1 ) T + x ∈ C 2 ∑ ( x − μ 2 ) ( x − μ 2 ) T ] w
S
w
=
∑
x
∈
C
1
(
x
−
μ
1
)
(
x
−
μ
1
)
T
+
∑
x
∈
C
2
(
x
−
μ
2
)
(
x
−
μ
2
)
T
S_{w}=\sum_{x\in C_{1}}({x}-\mu_{1})(x-\mu_{1})^{T}+\sum_{x\in C_{2}}({x}-\mu_{2})(x-\mu_{2})^{T}
S w = x ∈ C 1 ∑ ( x − μ 1 ) ( x − μ 1 ) T + x ∈ C 2 ∑ ( x − μ 2 ) ( x − μ 2 ) T
我们的优化目标是提升类间距离,减小类内距离,所以可最大化函数:
J
(
w
)
=
(
m
1
−
m
2
)
2
S
1
2
+
S
2
2
=
w
T
S
b
w
w
T
S
w
w
J(w)=\frac{(m_{1}-m_{2})^{2}}{S_{1}^{2}+S_{2}^{2}}=\frac{w^{T}S_{b}w}{w^{T}S_{w}w}
J ( w ) = S 1 2 + S 2 2 ( m 1 − m 2 ) 2 = w T S w w w T S b w
J
J
J
w
w
w
w
w
w
w
T
S
w
w
=
c
,
c
≠
0
w^{T}S_{w}w=c,c\neq 0
w T S w w = c , c ̸ = 0
J
(
w
)
J(w)
J ( w )
max
w
w
T
S
b
w
s
.
t
.
w
T
S
w
w
=
c
,
c
≠
0
\max_{w} w^{T}S_{b}w\\ s.t. \ w^{T}S_{w}w=c,c\neq 0
w max w T S b w s . t . w T S w w = c , c ̸ = 0
L
(
w
,
λ
)
=
w
T
S
b
w
−
λ
(
w
T
S
w
w
−
c
)
L(w,\lambda)=w^{T}S_{b}w-\lambda(w^{T}S_{w}w-c)
L ( w , λ ) = w T S b w − λ ( w T S w w − c )
∂
L
(
w
,
λ
)
∂
w
=
(
S
b
+
S
b
T
)
w
−
λ
(
S
w
+
S
w
T
)
w
=
2
S
b
w
−
2
λ
S
w
w
=
0
\frac{\partial L(w,\lambda)}{\partial w}=(S_{b}+S_{b}^{T})w-\lambda(S_{w}+S_{w}^{T})w\\ =2S_{b}w-2\lambda S_{w}w=0
∂ w ∂ L ( w , λ ) = ( S b + S b T ) w − λ ( S w + S w T ) w = 2 S b w − 2 λ S w w = 0
S
w
−
1
S
b
w
=
λ
w
S_{w}^{-1}S_{b}w=\lambda w
S w − 1 S b w = λ w
S
b
w
=
(
μ
1
−
μ
2
)
(
μ
1
−
μ
2
)
T
w
=
β
(
μ
1
−
μ
2
)
S_{b}w=(\mu_{1}-\mu_{2})(\mu_{1}-\mu_{2})^{T}w=\beta(\mu_{1}-\mu_{2})
S b w = ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T w = β ( μ 1 − μ 2 )
S
b
w
S_{b}w
S b w
μ
1
−
μ
2
\mu_{1}-\mu_{2}
μ 1 − μ 2
w
=
β
λ
S
w
−
1
(
μ
1
−
μ
2
)
w=\frac{\beta}{\lambda}S_{w}^{-1}(\mu_{1}-\mu_{2})
w = λ β S w − 1 ( μ 1 − μ 2 )
w
w
w
w
=
S
w
−
1
(
μ
1
−
μ
2
)
w=S_{w}^{-1}(\mu_{1}-\mu_{2})
w = S w − 1 ( μ 1 − μ 2 )
S
w
S_{w}
S w
S
w
=
U
Σ
V
T
S_{w}=U\Sigma V^{T}
S w = U Σ V T
S
w
−
1
=
V
Σ
−
1
U
T
S_{w}^{-1}=V\Sigma ^{-1}U^{T}
S w − 1 = V Σ − 1 U T https://blog.csdn.net/winycg/article/details/83005881
sklearn实现LDA线性判别:
import numpy as np
from sklearn. discriminant_analysis import LinearDiscriminantAnalysis
X = np. array( [ [ - 1 , - 1 ] , [ - 2 , - 1 ] , [ - 3 , - 2 ] , [ 1 , 1 ] , [ 2 , 1 ] , [ 3 , 2 ] ] )
y = np. array( [ 1 , 1 , 1 , 2 , 2 , 2 ] )
clf = LinearDiscriminantAnalysis( solver= 'svd' )
clf. fit( X, y)
print ( clf. predict( [ [ - 0.8 , - 1 ] ] ) )