最优化原理
如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。
无后效性
即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。
有重叠子问题
即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

2 斐波那契数列 $Fibonacci$

2.1 引入

有一头母牛，它每年年初生一头小母牛。每头小母牛从第二个年头开始，每年年初也生一头小母牛。请问在第n年的时候，共有多少头母牛？

2.2 定义

$fib(n) = fib(n - 1) + fib(n - 2)$

$0$ $1$ $1$ $2$ $3$ $5$ $8$ $13$ $21$ $34$

2.3 递归分治解决 $Recursion$

2.3.1 代码

int fib(n){
    return (n < 2) ? n : fib(n - 1) + fib(n - 2);
}

int fib(n){
    if(n < 2) return n;
    return fib(n - 1) + fib(n - 2);
}

2.3.2 时间复杂度分析

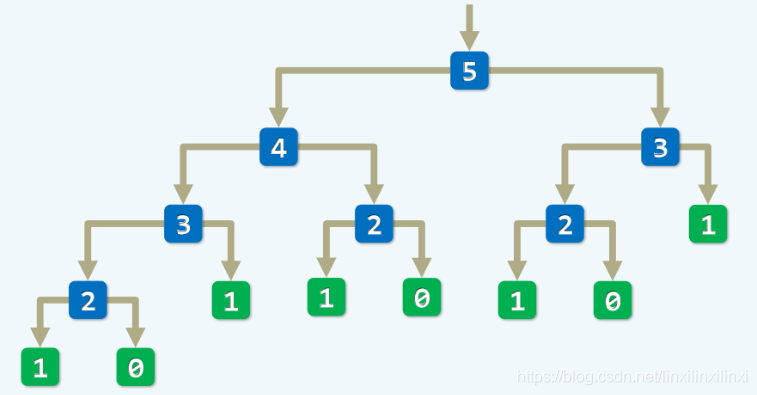
斐波那契数列递归求解

$T(n) = T(n - 1) + T(n - 2) + 1 \gt 2 \cdot T(n - 2) + 1 = O((\sqrt{2})^n)$

$T(n) = T(n - 1) + T(n - 2) + 1 = O(fib(n)) = O(\varPhi ^ n)$

$\varPhi = \frac{1 + \sqrt{5}}{2} = 1.618...$

$\varPhi^{36} \approx 2^{25}$

$\varPhi^{5} \approx 10$

凉了呀

2.4 解决方案

刚刚递归算法的不足之处在于重复计算了大量相同的子问题，浪费了大量时间

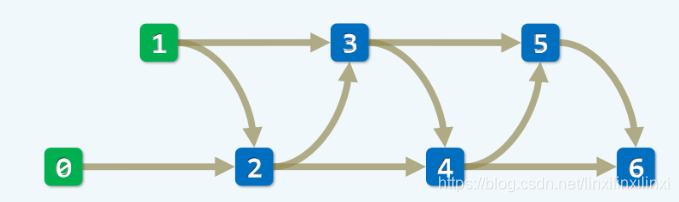
大量重复子问题

好记性不如烂笔头

记忆化搜索 $Memoization$

备忘录 $Look-up$ $Table$ $\to$ $Array$

用一个数组记录需要重复计算的子问题

这就是动态规划的第一种实现方式，也是最容易理解的写法：记忆化搜索

2.5 记忆化搜索

const int maxn = 1e6 + 5;
int f[maxn];
void init(){
    memset(f, -1, sizeof(f));
    f[0] = 0;
    f[1] = 1;
}
int fib(n){
    int& ret = f[n]
    if(ret != -1) return ret;
    ret = fib(n - 1) + fib(n - 2);
    return ret;
}

记忆化搜索后的计算过程

3 快速幂

3.1 问题描述

$a^{98765} = ???$

3.2 十进制快速幂

$a^{9\cdot10^4 + 8\cdot10^3 + 7\cdot10^2 + 6\cdot10^1 + 5\cdot10^0}$

十进制的快速幂

$(a^{10^4})^9 \cdot (a^{10^3})^8 \cdot (a^{10^2})^7 \cdot (a^{10^1})^6 \cdot (a^{10^0})^5$

3.3 二进制快速幂

根据计算机的储存特性，我们可以通过以二进制的快速幂来节省代码量，以及加快运算速度

二进制的快速幂

3.4 代码实现

ll quick_pow(ll a, ll b, ll mod){
    ll ret = 1;
    while(b){
        if(b&1) ret = (ret*a)%mod;
        a = (a*a)%mod;
        b >>= 1;
    }
    return ret;
}

4 最短向上路径问题

4.1 问题描述

SPU(Shortest Path Upward)

SPU

在某一个非负整数构成的 $n \times m$ 矩阵中，找出从最底层通往最高层的一条路径，使得路径总长（沿途所经整数的总和）最小（你只能走到上一层离你当前位置最近的三个位置）

4.2 暴力？

如果直接暴力枚举所有的路径

分析一下，时间复杂度大概是 $O(n\cdot3^m)$

可能，不太行

4.3 递归分治VS动态规划

4.3.1 递归分治

认真思考一下，发现可以这样递归来搞

$d^k(i) = w^k(i) + min\{d^{k - 1}(i - 1), d^{k - 1}(i), d^{k - 1}(i + 1)\}$

递归分治

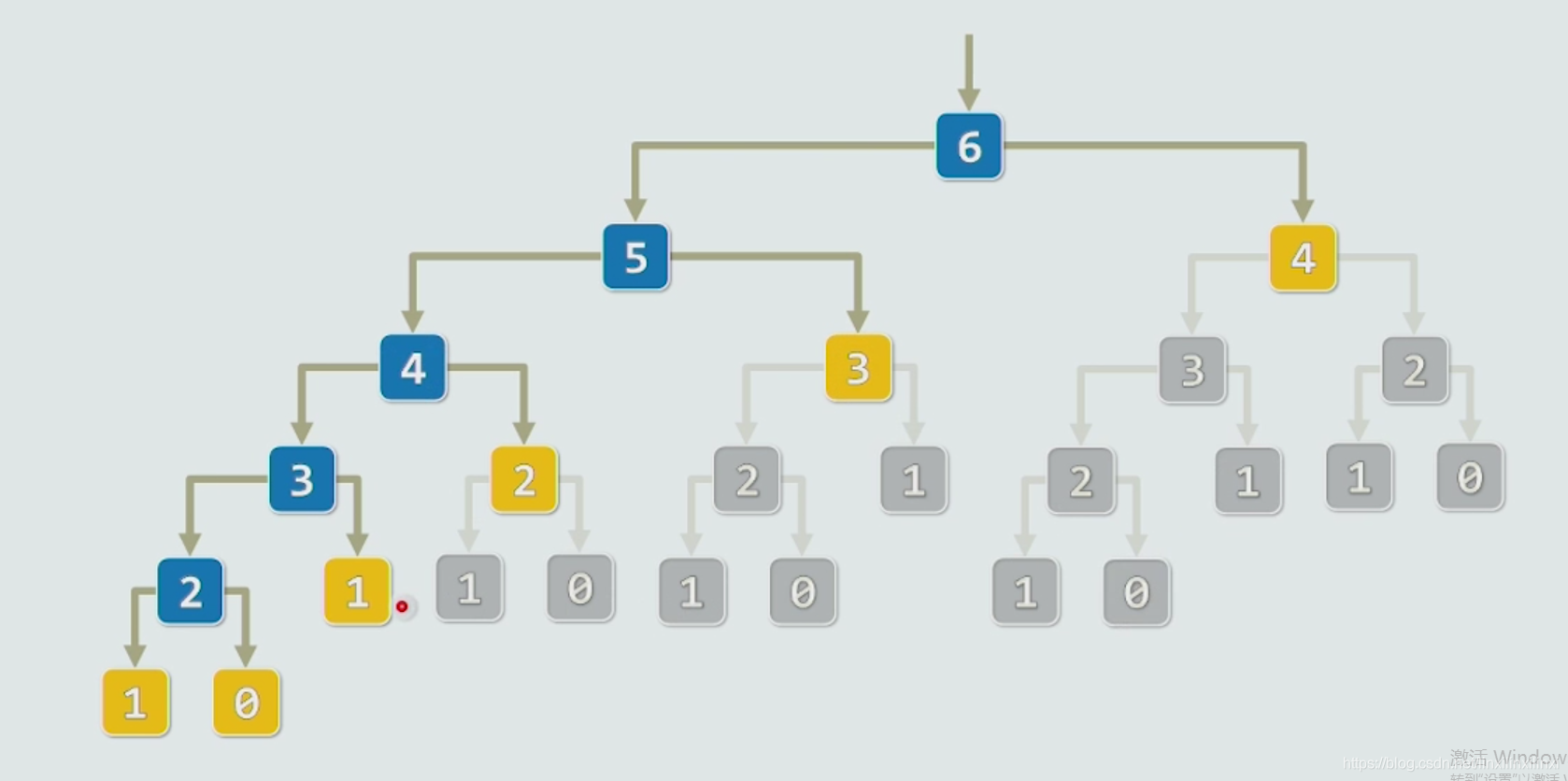
4.3.1.1 时间复杂度

这样我们看似使用了非常优美的递归来解决问题，但请冷静下来分析一下时间复杂度

分析一波

这样，我们会惊喜的发现：时间复杂度竟然和刚刚的暴力枚举算法是一样的

问题出现在哪里呢？

问题就出现在，我们重复计算了大量相同的问题，因此浪费了大量的时间

最高层的每一个位置我们只计算了一次，那么第二层平均每个会被上方的三个位置计算 $3$ 次，以此类推，第三层每个位置便会计算 $3^2$ 次…

如何解决呢？

4.3.1.2 记忆化搜索

我们发现，每一个位置的最优情况，只和它的位置有关，而跟他的内部路线与接下来的选择无关，这就是我们所说的无后效性

这样的话，我们可以开一个 $n\times m$ 的数组来储存所有位置的最优情况，然后将其初始化为 $undifine$ 状态

只有当这个位置没有被计算过的时候，我们才需要继续递归分治解决这个子问题，否则的话，直接使用之前计算好并储存下来的结果就好

这样的话每一个位置至多会被计算一次，这时候我们会发现时间复杂度已经降到了 $O(n*m)$

太秀了

4.3.2 正儿八经的动态规划

4.3.2.1 记忆化？

刚刚我们为什么需要记忆化呢

回想刚刚的问题，我们之所以需要递归分治并且记忆化的原因是：

我们需要的子问题的答案我们还没有计算出来

我们如何才能行云流水的推进过来，不需要询问没有解决的子问题呢

4.3.2.2 动态规划

我们考虑将刚才的过程颠倒过来

我们从底层往上层走：

动态规划
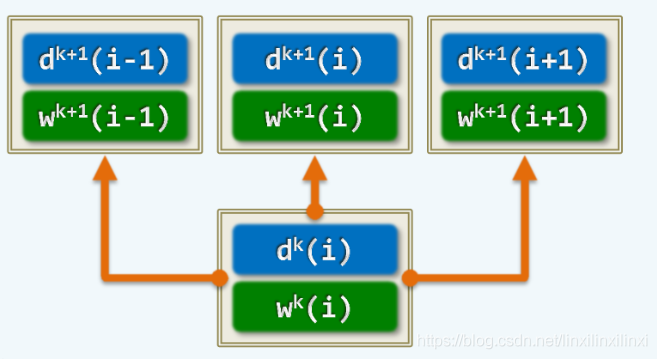
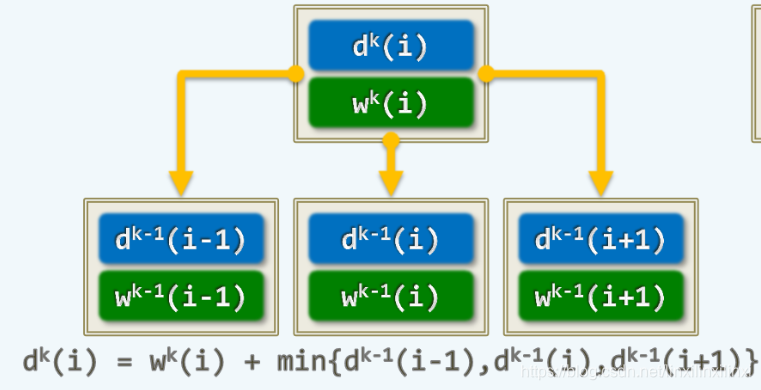
考虑dp转移式

$dp[k][i] = w[k][i] + min\{dp[k - 1][i - 1] + dp[k - 1][i] + dp[k - 1][i + 1]\}$

这样从底层往上层推进，我们会惊喜的发现，当我们推进到第 $i$ 层的时候，第 $i - 1$ 层的所有子问题都已经解决并且记录下了

而且我们发现每次只需要上一层的数据，并不需要再之前的所有子问题，我们还可以考虑滚动数组来降低空间复杂度

我真是个天才

5 最长曼哈顿路径问题

5.1 问题描述

LMP(Longest Manhattan Path)

在某一个非负整数构成的 $n\times m$ 矩阵中，找出从左上角通往右下角的一条路径，使得路径总长（沿途所经整数的总和）最大（你只能在矩阵内部向右走或者向下走）

LMP

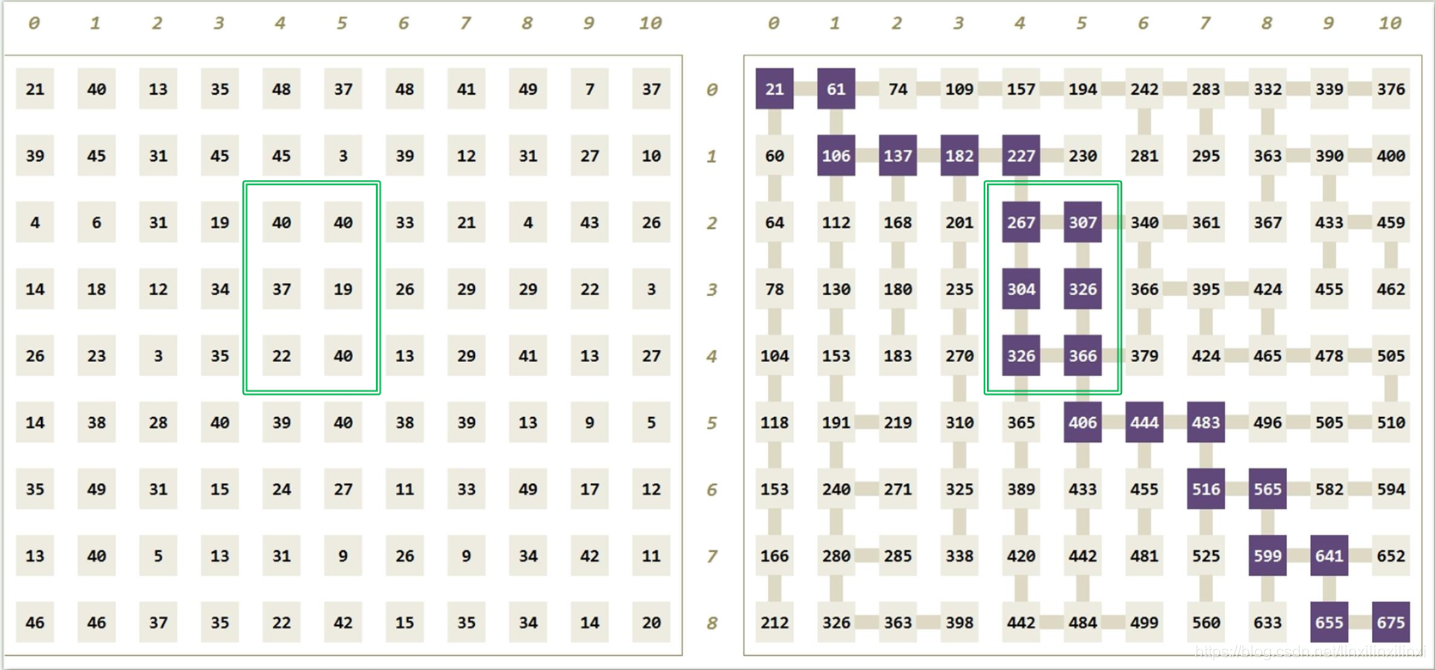
5.2 问题分析

5.2.1 考虑见神杀神的记忆化搜索

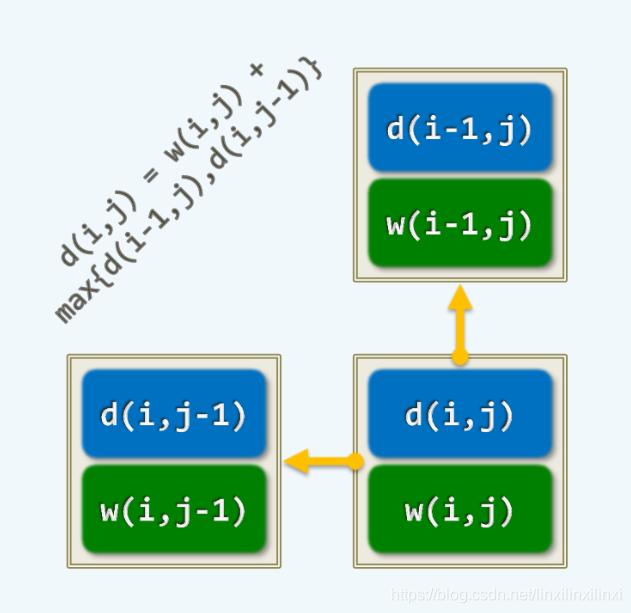
记忆化搜索

5.2.2 考虑一路高歌猛进的动态规划

动态规划

不多赘述

6 小结

我们发现，递归分治记忆化与动态规划本质上其实相差不多

而相对来说，记忆化搜索会更加好理解一些，而我们的第一反应也大多是记忆化搜索

递归是从最复杂的问题开始，将其分而治之，直到遇到平凡(Trival)的情况，然后一举攻克

而动态规划则是从最简单的情况开始，一层一层的逐步蚕食掉整个问题

我们如何写出动态规划的算法呢

我们将第一反应的从顶向下的递归算法理解，在实现的时候将其颠倒过来，写出一个从底向上的递推转移式

7 最长公共子序列

7.1 问题描述

LCS(Longest Common Subsequnce)

给定两个字符串，问两个字符串的公共子序列中，最长的长度为多少？是哪个？

7.1.1 子串 $Substring$

原串中连续的一部分

7.1.2 子序列 $Subsequnce$

原串中任意抽出任意多个字符（可以不连续，但先后顺序不能变），组成的字符串

7.1.3 举个栗子

举个栗子

在串 $NorthEastNormalUniversity$ 中

$East, tNor, Univers$ 为其子串

$NENU, oo, ttt, htly$ 为其子序列

7.2 样例及其分析

Example

7.3 解决问题

7.3.1 相同则减而治之

$s1[i] == s2[j]$

相同则减而治之

7.3.2 不同则分而治之

$s1[i] != s2[j]$

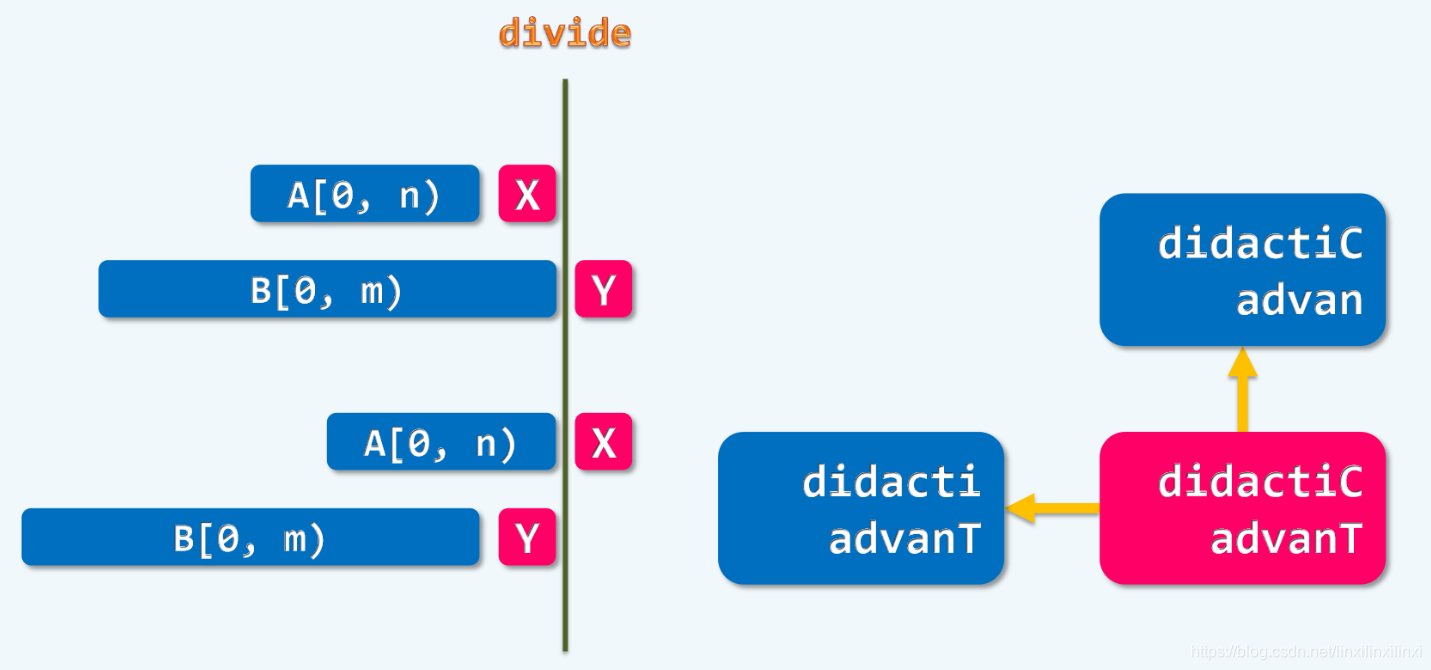
不同则分而治之

7.4 转移方程

scanf("%s", a + 1);
scanf("%s", a + 1);
int la = strlen(a + 1);
int lb = strlen(b + 1);
for(int i = 1; i <= la; ++i){
    for(int j = 1; j <= lb; ++j){
        if(a[i] == b[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
        else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
    }
}

7.5 dp表

dp表

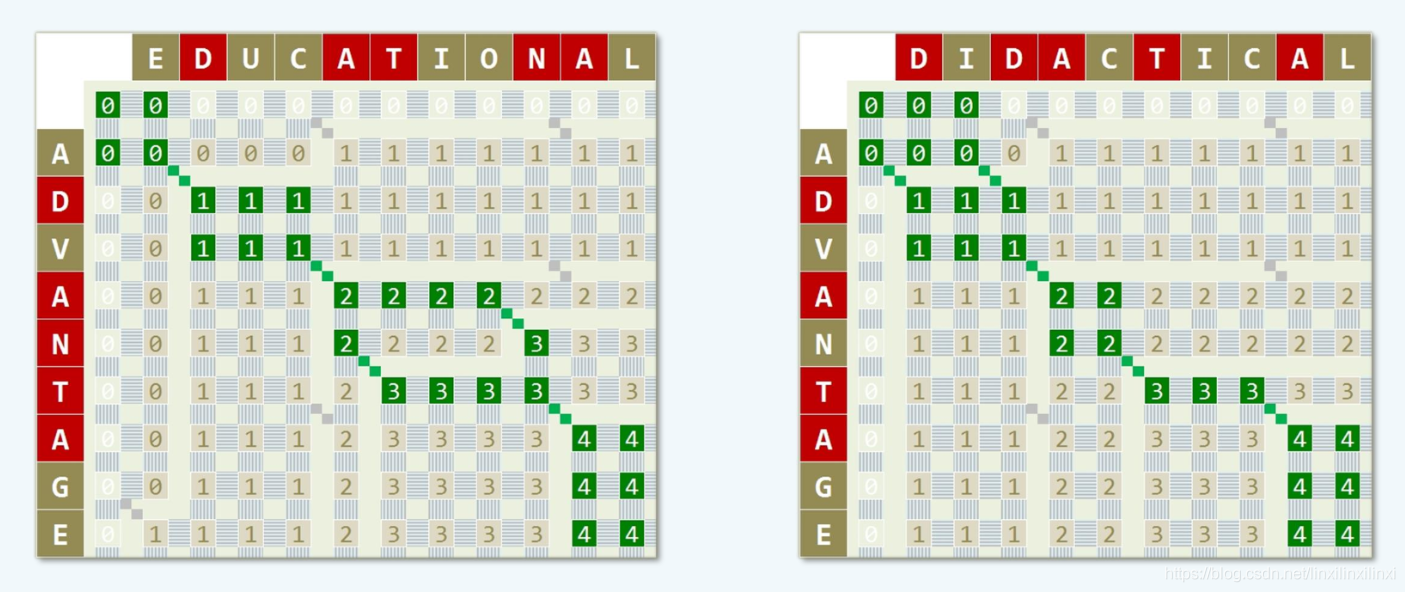
7.6 思考题

如何输出公共最长子序列的内容，以及统计最长公共子序列的个数

（一般来说，寻找长度之类的问题比较容易，追溯解就会比较难搞）
（一般来说，寻找任一最优解比较容易，最优解计数问题比较难搞）

8 背包问题（推荐背包九讲）

当前你有一个背包，有一系列的物品，物品都有自己的数量、重量 $w[i]$ 以及价值 $v[i]$ ，请问在不超过背包总重量 $W$ 的情况下获得的最大价值是多少（物品不能切分）

Bag

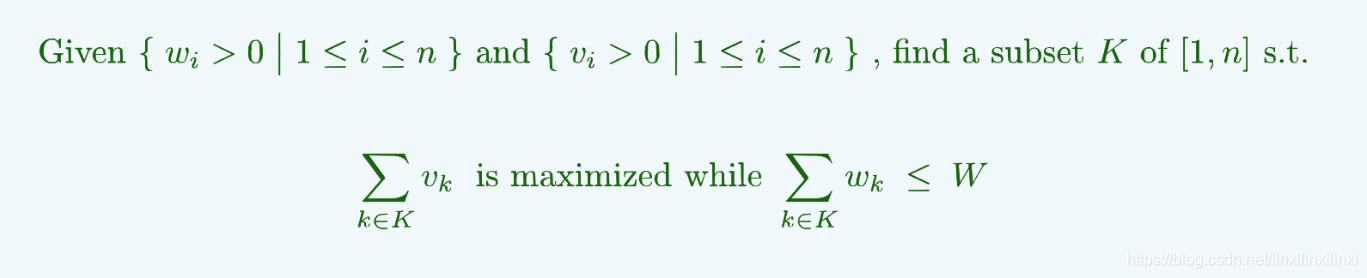
考虑贪心：

优先选择重量最小的
优先选择重量最大的
优先选择单位重量价值最高的

都很容易举出反例来

8.1 01背包问题

所有物品的数量都为1

8.1.1 选还是不选，这是一个问题

考虑动态规划，用数组 $dp[i][j]$ 表示只考虑前 $i$ 个物品，背包总承重为 $j$ 的情况下，能获得的最大价值

8.1.2 分析转移方程

对于每个物品我们都有两种情况

选：获得的最大价值为 $dp[i - 1][j - w[i]] + v[i]$
不选：获得的最大价值为 $dp[i - 1][j]$

这样的话，我们便很容易得到转移方程

$dp[i][j] = \begin{cases} dp[i - 1][j] & j < w[i] \\ max\{dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]\} & j >= w[i] \end{cases}$

8.1.3 dp表

dp表

8.1.4 代码实现

for(int i = 0; i < n; ++i){
    for(int j = w[i]; j <= W; ++j){
        dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
    }
}

优化空间

for(int i = 0; i < n; ++i){
    for(int j = W; j >= w[i]; --j){
        dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
    }
}

注意第二层循环顺序为倒序，因为每个物品只有一个，如果正序更新的话会出现当前物品多次选择的情况

8.2 完全背包问题

所有物品的数量都为无限多个

for(int i = 0; i < n; ++i){
    for(int j = w[i]; j <= W; ++j){
        dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
    }
}

8.3 多重背包问题

数量不定

需要考虑二进制优化

9 最长不降子序列LIS

9.1 定义

设有一个正整数序列 $a[n]: a_1, a_2 \cdots, a_n$ 对于下标 $i_1<i_2 < \cdots<i_h$ ，若有 $a_{i_1}, a_{i_2} \cdots a_{i_h}$ ,

则称序列 $a[n]$ 含有一个长度为 $h$ 的不下降子序列。

例如，对于序列 $3, 7, 9, 16, 38, 24, 27, 38, 44, 49, 21, 52, 63, 15$

对于下标 $i_1 = 1, i_2 = 4, i_3 = 5, i_4 = 9, i_5 = 13$

满足 $13 < 16 < 38 < 44 < 63$

则存在长度为5的不下降子序列。

9.2 问题描述

当给定序列 $a_1, a_2 \cdots a_n$ 后，请求出最长的不下降序列的长度

9.3 解决问题

9.3.1 $O(n^2)$ 的算法

对于任意的 $i$ , 定义 $dp[i]$ 是以 $a_i$ 结束的最长不下降子序列的长度，那么显然，问题的解为 $dp[n]$ 。

不妨假设，已求得以 $a_1,a_2, \cdots, a_{j − 1}$ 结束的最长不下降子序列的长度分别为 $dp[1],dp[2],...,dp[j−1]$

其中 $dp[1]=1$

那么对于 $a_i$ ，其中 $i < j − 1$ , 若 $a_i \le a_j$ ，则以 $a_i, a_j$ 结束的不下降子序列长度为的 $dp[i] + 1$

显然以 $a_i$ 结束的最长不下降子序列的长度

$dp[j] = max\{dp[i]\} + 1$

其中 $1 \le i \le j − 1, a_i \le a_j$

更新公式中每次都得从头遍历整个 $dp[i]$ ，所以算法复杂度为 $O(n^2)$

9.3.2 $O(nlogn)$ 算法

$O(nlogn)$ 的算法关键是它建立了一个数组 $b[]$

$b[i]$ 表示长度为 $i$ 的不下降序列中结尾元素的最小值

用 $k$ 表示数组目前的长度

算法完成后 $k$ 的值即为最长不下降子序列的长度。

不妨假设，当前已求出的长度为 $k$

则判断 $a[i]$ 和 $b[k]$ ：

如果 $b[k]\le a[i]$ ，即 $a[i]$ 大于长度为 $k$ 的序列中的最后一个元素

这样就可以使序列的长度增加 $1$ ，即 $k = k + 1$ 然后更新 $b[k] = a[i]$ ；

如果 $b[k] \gt a[i]$

那么就在 $b[1]\cdots b[k]$ 中找到最大的 $j$ 使得 $b[j] < a[i]$ ，即 $a[i]$ 大于长度为 $j$ 的序列的最后一个元素

显然， $b[j+1] \ge a[i]$ ，那么就可以更新长度为 $j + 1$ 的序列的最后一个元素，即 $b[j + 1] = a[i]$ 。

可以注意到： $b[i]$ 单调递增，很容易理解，长度更长了， $d[k]$ 的值是不会减小的，因此更新公式可以用二分查找，所以算法复杂度为 $O(logn)$ 。

代码实现

const int maxn = 5e4 + 10;
int a[maxn], b[maxn];
//用二分查找的方法找到一个位置，使得x>b[i - 1],并且x<b[i],并用x代替b[i]
int src(int x, int l, int r){
    while(l <= r){
        int mid = (l + r)/2;
        if(x >= b[mid]) l = mid + 1;
        else r = mid - 1;
    }
    return l;
}
int dp(int n){
    b[1] = a[1];
    int len = 1;
    for(int i = 2; i <= n; ++i){
        if(a[i] >= b[len]) b[++len] = a[i]; //如果a[i]比b数组中最大的数还大，便将此数直接插入到b数组后面
        else b[src(a[i], 1, len)] = a[i]; //二分查找第一个比a[i]大的位置并且让a[i]代替这个位置
    }
    return len;
}

ACM动态规划基础篇

文章目录

1 前言

1.1 什么是动态规划

1.2 什么时候要用动态规划

2 斐波那契数列 F i b o n a c c i Fibonacci Fibonacci