吴恩达第一门-神经网络和深度学习第二周6-10学习笔记

神经网络和深度学习第二周6-10学习笔记

6.更多导数的例子

在本节中，为上一节的导数学习提供更多的例子。在上一节中，我们复习了线性函数的求导方法，其导数值在各点中是相等的。本节以y=a^2这一二次函数为例，介绍了导数值在各点处发生变化时的求导方法。求导大家都会，y=x ^3的导数是3x ^2,y=x ^2的导数是2x，y=lnx的导数是1/x。这里不做赘述。

7.计算图

一个神经网络的计算，都是按照前向或反向传播过程组织的。前向传播过程就是从输入到输出的过程，将输入通过计算得到输出值。而后向传播一般用来计算导数值，或者说是计算出输出对应的各个神经元中值的梯度。在这节举一个由输入正向计算出输出值的例子。
在这里插入图片描述
设有一个三元函数J(a,b,c)=3(a+bc),要完成该计算需要进行三个步骤，分别是u=bc,v=a+u,J=wv。将这三步填入上图的计算图中，蓝线的传递方向即为正向传播方向。将b,c值代入u第一个方框，计算u值为6，再将a,u值代入第二个方框计算出v值为11，最后将v值代入第三个方框计算出J值为33。这就是一个简单的正向传播的计算过程举例。图中的蓝线为反向传播过程，将在下一节中进行介绍。

8.使用计算图求导数

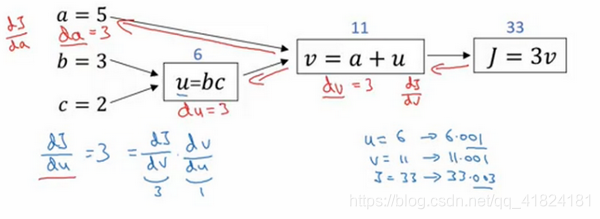
在这里插入图片描述
上一节介绍的是一个简单的正向传播过程，这一节我们对上一张配图中的蓝线过程——反向传播过程进行举例。我们将通过这个反向过程计算出J的各级导数。因为大家对求导都十分熟悉，这里就不以极限的形式具体展开每一步的详细求导过程了。根据三个方框图，我们可以很容易地计算出J对v的导数，v对于u的导数，u对于b的导数，分别为： $\frac{d J}{d v}=3$ $\frac{d v}{d u}=1$ $\frac{d u}{d b}=c=2$ 根据链导法则： $\frac{\partial J}{\partial b}=\frac{d J}{d v}*\frac{d v}{d u}*\frac{d u}{d b}=6$ ,同理可得出： $\frac{\partial J}{\partial c}=\frac{d J}{d v}*\frac{d v}{d u}*\frac{d u}{d b}=9$
这是一个计算流程图，就是正向过程可以计算来计算成本函数J，如果想要优化某个函数，然后反向从右到左计算导数，对各个参数进行优化。

9.逻辑回归中的梯度下降

本节我们主要学习了如何通过计算偏导数来实现逻辑回归的梯度下降算法。

回顾

首先我们先来复习一下逻辑回归的公式，
$\widehat{y}=\sigma (z)=a$
$\sigma (z)=\frac{1}{1+e^{z}}$
$z=w^{T}+b$
损失函数 $L(\widehat{y}^{(i)},y^{(i)})=-y^{(i)}*\log\widehat{y}^{(i)}-(1-y^{(i)})*\log(1-\widehat{y}^{(i)})$
其中a是逻辑回归的输出，y是样本的实际值。

梯度下降法

本节讨论的单一样本的梯度下降法应用，所以单一样本的损失函数为 $L(\widehat{y}^{(i)},y^{(i)})=-y*\log(a)-(1-y)*\log(1-a)$
在这里插入图片描述
梯度下降法的目的是为了使逻辑回归的代价函数最小化，我们需要做的仅仅是修改w参数和b参数的值。自然而然地可以想出我们要对L(a,y)求导，最终目的是求出其对于w,b的导数。我们首先要做的就是求出L(a,y)对于a,z的导数，过程如下
$da=\frac{dL}{da}=-\frac{y}{a}+\frac{1-y}{1-a}$
$dz=\frac{dL}{dz}=\frac{dL}{da}*\frac{da}{dz}=a-y$
$db=\frac{dL}{db}=a-y$
$dw1=x1*dz$
在这里插入图片描述
在计算完成了导数之后，我们接下来需要做的就是一次次更新w1=w1- $\alpha$ *w1,w2=w2- $\alpha$ *w2,b=b- $\alpha$ *b

在本节中我们学习了怎样计算导数，并且实现针了对单个训练样本的逻辑回归的梯度下降算法。

10. m 个样本的梯度下降

在上一节中我们学习了如何针对单个训练样本的逻辑回归的梯度下降算法，本节中我们将梯度下降算法用于多样本中。
损失函数的公式为：
$J(w,b)=\frac{1}{m}*\sum_{i=1}^{m}L(a^{(i)},y^{(i)})$
伪代码如下

J=0;dw1=0;dw2=0;db=0;//初始化
for i = 1 to m
    z(i) = wx(i)+b;
    a(i) = sigmoid(z(i));
    J += -[y(i)log(a(i)))+(1-y(i)*log(1-a(i))];
    dz(i) = a(i)-y(i);
    dw1 += x1(i)dz(i);
    dw2 += x2(i)dz(i);
    db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db

但是这种算法存在着一个缺点，我们可以看到在算法中我们需要两个for循环，第一个for循环用于遍历m个训练样本，第二个for循环用于遍历每个训练样本的各个特征。(上述代码中只有两个特征，没有使用第二个for循环)
在代码中使用显示的for循环使你的算法很低效，同时在深度学习领域会有越来越大的数据集。所以使你的算法中没有显式的for循环会是十分重要的，并且会帮助我们适用于更大的数据集。
为了尽可能地减少for循环的出现，我们将在下一节中学习向量化技术，期待其能使我们摆脱for循环的困扰。