1. 硬间隔最大化:
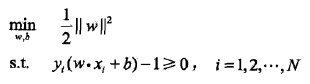
怎么得到的?自己推导,可参考下图推:
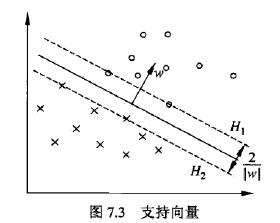
上述问题如何求解?
引入Lagrange function:
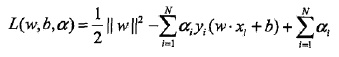
一系列推导之后,自己推导:

原始问题:
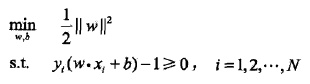
对偶优化问题:
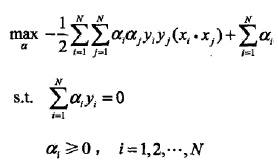
对偶问题求最最优:
怎么求的SMO算法如何实现,先等着?
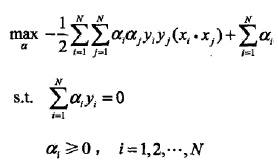
对α的解为:
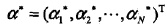
根据KKT条件,求得 和 :
KKT条件:
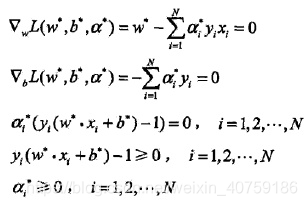
关注互补对偶条件如何得到的?
根据KKT条件,求得
和
:
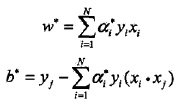
如何推导,自己推(选择一个
> 0)
2. 软间隔最大化
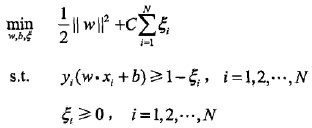
转化为对偶问题:
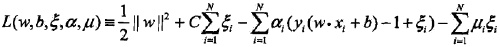
推导之后:
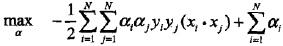
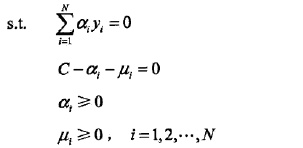
进一步转化:
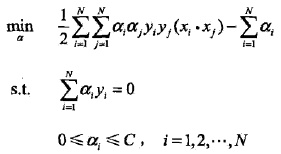
看到没?硬的和软的对偶函数之间区别,只在于
的区域,但是转换为原目标最优还需要满足KKT条件。
对α的解为:
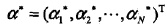
根据KKT条件,求得 和 :
KKT条件:
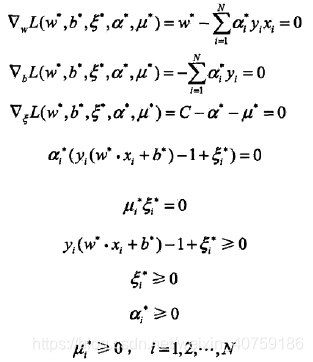
比较好求?
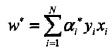
如何求
?
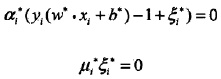
找一个0<
<C,则
= 0:
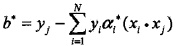
由于:
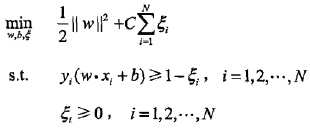
对b的解并不唯一,所以实际计算时可以取在所有符合条件的样本点上的平均值。
这句话的理解:
是松弛因子,允许有些点在margin之内,0=<
,
=0,即
=C。
=C是有loss的。
需要分割尽量开,同时允许有一些异常点,异常点发生在
=C的点,0<
<C的点都是支持向量,因为有
=C的点存在,导致b有多个解,所以b要取所有b的均值,
=0的点没有用。
3. Hinge Loss
软间隔
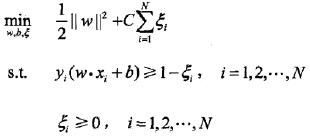
Hinge Loss
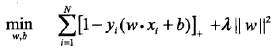
Hinge Loss就相当于松弛因子
对于间距大于一定程度的点,就没有loss,就不用松弛。
正则化的作用相当于把分类的距离拉大。
4. 核函数
没啥东西,目标函数暴走,目标函数只需要比较对象的距离,而不是其本身,利用目标函数的这个弱点使用了kernel trick。
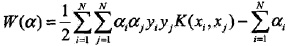
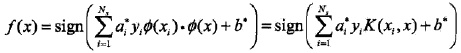
5. SMO算法
SMO算法要解如下凸二次规划的对偶问题:
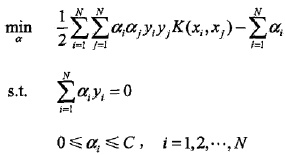
我们的解要满足的KKT条件的对偶互补条件为:
根据这个KKT条件的对偶互补条件,我们有:
由于
,我们令
,则有:
SMO算法的基本思想
SMO算法是一种启发式算法,其基本思路是:如果所有变量的解都满足此最优化问题的KKT条件(Karush-Kuhn-Tuckerconditions),那么这个最优化问题的解就得到了。
整个SMO算法包括两个部分:求解两个变量二次规划的解析方法***和***选择变量的启发式方法。
求解两个变量二次规划的解析方法
子问题如下:
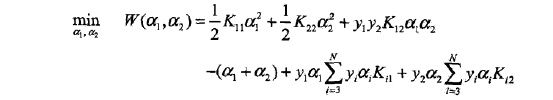
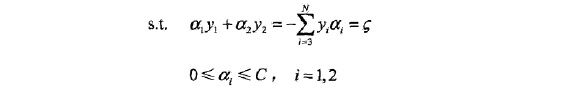
由于只有两个变量 [
,
] ,约束可以用二维空间中的图形表示(如图所示)。

左图:
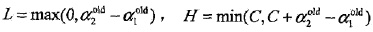
右图:
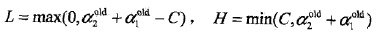
简化理解:
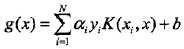

沿着约束方向未经剪辑时的解是:
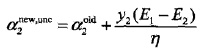

经剪辑后的解是:
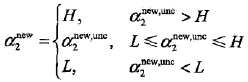
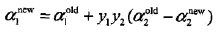
变量的选择方法
SMO算法在每个子问题中选择两个变量优化,其中至少一个变量是违反KKT条件的。
1.第1个变量的选择
SMO称选择第1个变量的过程为外层循环。外层循环在训练样本中选取违反KKT条件最严重的样本点,并将其对应的变量作为第1个变量。具体地,检验训练样本点支持向量机(
,
)是否满足KKT条件,即
该检验是在支持向量机
范围内进行的。在检验过程中,外层循环首先遍历所有满足条件
支持向量机的样本点,即在间隔边界上的支持向量点,检验它们是否满足KKT条件。如果这些样本点都满足KKT条件,那么遍历整个训练集,检验它们是否满足KKT条件。
如何选择违反KKT条件最严重的样本点?
# 接下来需要选择违反KKT条件最严重的那个alphas[i]
# 满足KKT条件的三种情况
# 1.yi*f(i)>=1 且 alpha=0,样本点落在最大间隔外(分类完全正确的那些样本)
# 2.yi*f(i)==1 且 alpha<C,样本点刚好落在最大间隔边界上
# 3.yi*f(i)<=1 且 alpha==C,样本点落在最大间隔内部
# 情况2,3中的样本点也叫做支持向量
# 违背KKT条件的三种情况(与上面相反)
# 因为 y[i]*Ei = y[i]*f(i) - y[i]^2 = y[i]*f(i) - 1, 因此
# 1.若yi*f(i)<0,则y[i]*f(i)<1,如果alpha<C,那么就违背KKT(alpha==C 才正确)
# 2.若yi*f(i)>0,则y[i]*f(i)>1,如果alpha>0,那么就违背KKT(alpha==0才正确)
# 3.若yi*f(i)==0,那么y[i]*f(i)==1,此时,仍满足KKT条件,无需进行优化
2.第2个变量的选择
SMO称选择第2个变量的过程为内层循环。假设在外层循环中已经找到第1个变量
,现在要在内层循环中找第2个变量
。第2个变量选择的标准是希望能使
有足够大的变化。
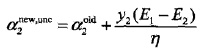
第二个变量
的选择标准是让|
−
|有足够大的变化。由于
定了的时候,
也确定了,所以要想|
−
|最大,只需要在
为正时,选择最小的
作为
, 在
为负时,选择最大的
作为
,可以将所有的
保存下来加快迭代。
如果内存循环找到的点不能让目标函数有足够的下降, 可以采用遍历支持向量点来做 ,直到目标函数有足够的下降, 如果所有的支持向量做 都不能让目标函数有足够的下降,可以跳出循环,重新选择 .
3.计算阈值 和差值
在每次完成两个变量的优化之后,需要重新计算阈值b。当
时,我们有
于是新的
为:
计算出
为:
可以看到上两式都有
,因此可以将
用
表示为:
同样的,如果
, 那么有:
最终的
为:
得到了
我们需要更新
:
其中,S是所有支持向量
的集合.
SMO实现:
数据集:
https://pan.baidu.com/s/1_3OgMSvuUHiZAZLdL4bVUw
from numpy import *
import matplotlib.pyplot as plt
def loadDataSet(fileName):
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
linArr = line.strip().split('\t')
dataMat.append([float(linArr[0]), float(linArr[1])])
labelMat.append(float(linArr[2]))
return dataMat, labelMat
def kernelTrans(X, sampleX, kernelOp):
"""
计算K(train_x,x_i)
:param X:[n_samples, n_features] 保存训练样本的矩阵
:param sampleX: [1,n] 某一样本矩阵
:param kernelOp: 携带核信息的元组:参数一给定核的名称;后面参数为核函数可能需要的可选参数
:return: K (numSamples,1)=shape(K)
"""
m = shape(X)[0] # 样本数
K = mat(zeros((m, 1)))
if kernelOp[0] == 'linear': # 线性核
K = X * sampleX.T
elif kernelOp[0] == 'rbf': # 高斯核
sigma = kernelOp[1]
if sigma == 0: sigma = 1
for i in range(m):
deltaRow = X[i, :] - sampleX
K[i] = exp(deltaRow * deltaRow.T / (-2.0 * sigma ** 2))
else:
raise NameError('Not support kernel type! You can use linear or rbf!')
return K
class SvmStruct:
def __init__(self, dataMatIn, labelMat, C, toler, kernelOp):
"""
初始化所有参数
:param dataMatIn: 训练集矩阵
:param labelMat: 训练集标签矩阵
:param C: 惩罚参数
:param toler: 误差的容忍度
:param kernelOp: 存储核转换所需要的参数信息
"""
self.train_x = dataMatIn
self.train_y = labelMat
self.C = C
self.toler = toler
self.numSamples = shape(dataMatIn)[0] # 样本数
self.alphas = mat(zeros((self.numSamples, 1))) # 初始化待优化的一组alpha
self.b = 0
self.errorCache = mat(zeros((self.numSamples, 2))) # 第1列为有效标志位(表示已经计算),第2列为误差值
self.K = mat(zeros((self.numSamples, self.numSamples)))
# 计算出训练集 train_x 与每个样本X[i,:]的核函数转换值,并按列存储,那么共有 numSamples 列
# 这样提取存储,方便查询使用,避免重复性计算,提高计算效率
for i in range(self.numSamples):
self.K[:, i] = kernelTrans(self.train_x, self.train_x[i, :], kernelOp)
def calcError(svm, k):
"""
计算第k个样本的预测误差
:param k:
:return:
"""
# 不使用核函数的版本
# fxk = float(multiply(svm.alphas, svm.train_y).T * (svm.train_x * svm.train_x[k, :].T)) + svm.b
fxk = float(multiply(svm.alphas, svm.train_y).T * svm.K[:, k] + svm.b) # 使用核函数得出的预测值
Ek = fxk - float(svm.train_y[k])
return Ek
def selectJ(svm, i, Ei):
"""
寻找第二个待优化的alpha,并具有最大步长
:param i: 第一个alpha值的下标
:param svm:
:param Ei:第一个alpha值对应的Ei
:return:
"""
maxK = 0
maxStep = 0
Ej = 0
validEcacheList = nonzero(svm.errorCache[:, 0].A)[0] # 从误差缓存矩阵中 得到记录所有样本有效标志位的列表(注:存的是索引)
if (len(validEcacheList)) > 1: # 选择具有最大步长的 j
for k in validEcacheList:
if k == i:
continue
Ek = calcError(svm, k)
step = abs(Ei - Ek)
if (step > maxStep): # 选择 Ej 与 Ei 相差最大的那个 j,即步长最大
maxK = k
maxStep = step
Ej = Ek
return maxK, Ej
else: # 第一次循环采用随机选择法
l = list(range(svm.numSamples))
# 排除掉已选的 i
seq = l[:i] + l[i + 1:]
j = random.choice(seq)
Ej = calcError(svm, j)
return j, Ej
def cliAlpha(alpha, L, H):
"""
控制alpha在L到H范围内
:param alpha: 待修正的alpha
:param H: 上界
:param L: 下界
:return:
"""
if alpha > H:
alpha = H
if alpha < L:
alpha = L
return alpha
def updateError(svm, k):
"""
第k个样本的误差存入缓存矩阵,再选择第二个alpha值用到
:param svm:
:param k: 样本索引
:return:
"""
Ek = calcError(svm, k)
svm.errorCache[k] = [1, Ek]
def innerL(svm, i):
"""
:param i: 第一个alpha值的下标
:param svm:
:return: 返回是否选出了一对 alpha 值
"""
Ei = calcError(svm, i) # 计算第一个alpha值对应样本的预测误差
# 接下来需要选择违反KKT条件最严重的那个alphas[i]
# 满足KKT条件的三种情况
# 1.yi*f(i)>=1 且 alpha=0,样本点落在最大间隔外(分类完全正确的那些样本)
# 2.yi*f(i)==1 且 alpha<C,样本点刚好落在最大间隔边界上
# 3.yi*f(i)<=1 且 alpha==C,样本点落在最大间隔内部
# 情况2,3中的样本点也叫做支持向量
# 违背KKT条件的三种情况(与上面相反)
# 因为 y[i]*Ei = y[i]*f(i) - y[i]^2 = y[i]*f(i) - 1, 因此
# 1.若yi*f(i)<0,则y[i]*f(i)<1,如果alpha<C,那么就违背KKT(alpha==C 才正确)
# 2.若yi*f(i)>0,则y[i]*f(i)>1,如果alpha>0,那么就违背KKT(alpha==0才正确)
# 3.若yi*f(i)==0,那么y[i]*f(i)==1,此时,仍满足KKT条件,无需进行优化
if ((svm.train_y[i] * Ei < -svm.toler) and (svm.alphas[i] < svm.C) or (svm.train_y[i] * Ei > svm.toler) and (
svm.alphas[i] > 0)): # 选择违反KKT条件最严重的alpha[i]
j, Ej = selectJ(svm, i, Ei) # 选择第二个alpha值的下标以及得到其对应的样本的预测误差
alphaIold = svm.alphas[i].copy() # 记录更新前的alpha值
alphaJold = svm.alphas[j].copy() # 记录更新前的alpha值
# 确定 alpha 值 的上下界
if (svm.train_y[i] != svm.train_y[j]):
L = max(0, alphaJold - alphaIold)
H = min(svm.C, svm.C + alphaJold - alphaIold)
else:
L = max(0, alphaIold + alphaJold - svm.C)
H = min(svm.C, alphaIold + alphaJold)
if L == H: return 0
# 不使用核函数版本
# X_i = svm.train_x[i, :]
# X_j = svm.train_x[j, :]
# eta = 2.0 * X_i * X_j.T - X_i * X_i.T - X_j * X_j.T
# 使用核函数版本
eta = svm.K[i, i] + svm.K[j, j] - 2.0 * svm.K[i, j] # 计算eta=k_ii+k_jj-2*k_ij
if eta <= 0: print("WARNING eta<=0");return 0
svm.alphas[j] += svm.train_y[j] * (Ei - Ej) / eta # 计算出最优的alpha_j,也就是第二个alpha 值
svm.alphas[j] = cliAlpha(svm.alphas[j], L, H) # 得到修正范围后的 alpha_j
if abs(svm.alphas[j] - alphaJold) < 0.00001: # alpha_j 变化太小,直接返回
updateError(svm, j)
return 0
svm.alphas[i] += svm.train_y[i] * svm.train_y[j] * (alphaJold - svm.alphas[j]) # 由 alpha_j 推出 alpha_i
updateError(svm, i) # 更新样本 i 的预测值误差
# 不使用核函数版本
# b1 = b - Ei - label_i * (alpha_i - alphaIold) * X_i * X_i.T - label_j * (alpha_j - alphaJold) * X_i * X_j.T
# b2 = b - Ej - label_i * (alpha_i - alphaIold) * X_i * X_j.T - label_j * (alpha_j - alphaJold) * X_j * X_j.T
# 使用核函数版本
# 计算阈值
b1 = - Ei - svm.train_y[i] * (svm.alphas[i] - alphaIold) * svm.K[i, i] - svm.train_y[j] * (
svm.alphas[j] - alphaJold) * svm.K[i, j] + svm.b
b2 = - Ej - svm.train_y[i] * (svm.alphas[i] - alphaIold) * svm.K[i, j] - svm.train_y[j] * (
svm.alphas[j] - alphaJold) * svm.K[j, j] + svm.b
if (0 < svm.alphas[i]) and (svm.alphas[i] < svm.C): # alpha_i 不在边界上,b1有效
svm.b = b1
elif (0 < svm.alphas[j]) and (svm.alphas[j] < svm.C): # alpha_j 不在边界上,b2有效
svm.b = b2
else: # alpha_j、alpha_j 都在边界上,阈值取中点
svm.b = (b1 + b2) / 2
updateError(svm, j)
updateError(svm, i)
return 1 # 一对alphas值已改变
else:
return 0
def smoP(dataSet, classLabels, C, toler, maxIter, KTup=('linear', 1.0)):
svm = SvmStruct(mat(dataSet), mat(classLabels).T, C, toler, KTup)
iter = 0
entireSet = True # 是否遍历所有alpha
alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: # 对整个训练集遍历
for i in range(svm.numSamples):
alphaPairsChanged += innerL(svm, i)
print('---iter:%d entire set, alpha pairs changed:%d' % (iter, alphaPairsChanged))
else: # 对非边界上的alpha遍历(即约束在0<alpha<C内的样本点)
nonBoundIs = nonzero((svm.alphas.A > 0) * (svm.alphas.A < svm.C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(svm, i)
print('---iter:%d non boundary, alpha pairs changed:%d' % (iter, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif (alphaPairsChanged == 0):
entireSet = True
return svm
def calcWs(alphas, dataArr, labelArr):
"""
计算W
:param alphas: 大部分为0,非0的alphas对应的样本为支持向量
:param dataArr:
:param classLabels:
:return:
"""
X = mat(dataArr)
labelMat = mat(labelArr).T
m, n = shape(X)
w = zeros((n, 1))
for i in range(m): ## alphas[i]=0的无贡献
w += multiply(alphas[i] * labelMat[i], X[i, :].T)
return w
def plotSVM():
dataMat, labelMat = loadDataSet('testSet.txt')
svm = smoP(dataMat, labelMat, 0.6, 0.001, 50)
classified_pts = {'+1': [], '-1': []}
for point, label in zip(dataMat, labelMat):
if label == 1.0:
classified_pts['+1'].append(point)
else:
classified_pts['-1'].append(point)
fig = plt.figure()
ax = fig.add_subplot(111)
for label, pts in classified_pts.items():
pts = array(pts)
ax.scatter(pts[:, 0], pts[:, 1], label=label)
supportVectorsIndex = nonzero(svm.alphas.A > 0)[0]
for i in supportVectorsIndex:
plt.plot(svm.train_x[i, 0], svm.train_x[i, 1], 'oy')
w = calcWs(svm.alphas, dataMat, labelMat)
x1 = min(array(dataMat)[:, 0])
x2 = max(array(dataMat)[:, 0])
a1, a2 = w
y1, y2 = (-float(svm.b) - a1 * x1) / a2, (-float(svm.b) - a1 * x2) / a2
ax.plot([x1, x2], [y1, y2])
plt.show()
plotSVM()
def testSVMWithLinearKernel():
dataArr, labelArr = loadDataSet('testSet.txt')
svm = smoP(dataArr, labelArr, 0.6, 0.001, 50)
dataMat = mat(dataArr)
labelMat = mat(labelArr).T
svInd = nonzero(svm.alphas.A > 0)[0]
sVs = dataMat[svInd]
labelSv = labelMat[svInd]
print("there are %d Support Vector" % shape(sVs)[0])
m, n = shape(dataMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs, dataMat[i, :], ('linear', 1.0))
predict = kernelEval.T * multiply(labelSv, svm.alphas[svInd]) + svm.b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is : %f" % (errorCount / m))
# testSVMWithLinearKernel()
# dataMat, train_y = loadDataSet('testSet.txt')
# b, alphas = smoP(dataMat, train_y, 0.6, 0.001, 50)
# ws = calcWs(alphas, dataMat, train_y)
# errorCount = 0
# for i in range(shape(dataMat)[0]):
# a = mat(dataMat)[i] * mat(ws) + b
# if sign(a) != train_y[i]:
# errorCount += 1
# print("the training error rate is : %f" % (errorCount / shape(dataMat)[0]))
# print(a) # 预测的值 a>0 ==1 a<0 -1
# print(train_y[0])
def testRbf(k1=1.3):
dataArr, labelArr = loadDataSet('testSetRBF.txt')
svm = smoP(dataArr, labelArr, 200, 0.0001, 100, ('rbf', k1))
dataMat = mat(dataArr)
labelMat = mat(labelArr).T
svInd = nonzero(svm.alphas.A > 0)[0]
sVs = dataMat[svInd]
labelSv = labelMat[svInd]
print("there are %d Support Vector" % shape(sVs)[0])
m, n = shape(dataMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs, dataMat[i, :], ('rbf', k1))
predict = kernelEval.T * multiply(labelSv, svm.alphas[svInd]) + svm.b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is : %f" % (errorCount / m))
Reference:
https://blog.csdn.net/u013534680/article/details/80371680
http://www.hankcs.com/ml/support-vector-machine.html#h3-3