SVM个人学习总结

如题，本文是对SVM学习总结，主要目的是梳理SVM推导过程,以及记录一些个人理解。

1.主要参考资料

[1]Corres C. Support vector networks[J]. Machine Learning, 1995, 20(3):273-297.
[2]Platt J C. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines[C]// Advances in Kernel Methods-support Vector Learning. 1998:págs. 212-223.
[3]结构之法算法之道:支持向量机通俗导论（理解SVM的三层境界)
[4]Free Mind：支持向量机系列
[5]JerryLead：支持向量机系列
[6]周志华：《机器学习》
[7]zouxy09的专栏：机器学习算法与Python实践之（四）支持向量机（SVM）实现
[8]Jasper:SVM入门（一）至（三）Refresh

2.推导思路简析

1.线性可分基本模型（几何问题，凸优化问题，不等式约束）

2.对偶问题：拉格朗日乘子法，KKT条件

3.SMO算法：求解对偶问题

4.软间隔：引入松弛变量和惩罚函数

5.线性不可分：映射与核函数

6.多分类问题

3.1 线性可分基本模型

（1）问题描述：对于给定的两类训练样本，找到一个超平面将其分成两类。

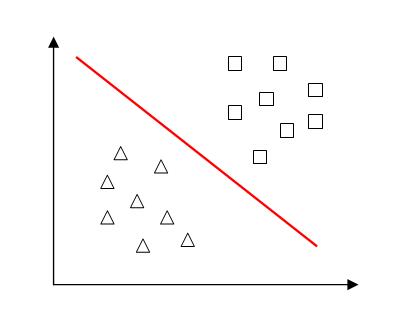
在样本空间中，超平面可以用如下线性方程描述：\[w^T x + b = 0 \tag{3.1.1} \]

SVM的目的：寻找最优的超平面(w,b)。

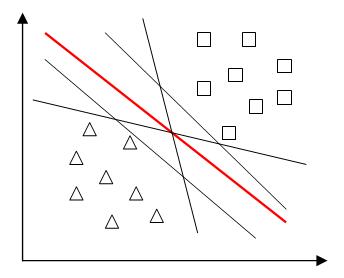
（2）如果仅仅是为了把两类训练样本分开，可以有多个超平面将其分开，但是我们追求最好的超平面，以便在预测时有更强的泛化能力。从直观上看，当两类样本点均远离超平面时，超平面分类效果更好，即所有样本点到超平面的最小距离越大，超平面分类效果越好。

样本点到超平面的距离可分为函数距离和几何距离。
函数距离： \[r_f = y * (w^T x + b) = y*f(x)\tag{3.1.2}\]
几何距离： \[r_g = \frac{y * (w^T x + b)}{||w||} =\frac{ y*f(x)}{||w||}\tag{3.1.3}\]
由于y的取值是1或-1，并且与f(x)同号，所以函数间隔实际上是|f(x)|,其缺陷是当w和b成比例变化时，超平面不变，但是函数距离会变化，因此不便于统一评价。
几何距离是直观上点到超平面的距离，仅与超平面本身有关，更适合做超平面的评价指标。

任意样本点x到超平面$w^T x + b = 0$的距离: \[ d = {|w^T x + b|}{||w||} \tag{3.1.4}\]

式（3.1.4）几何证明：设超平面方程为$w^T x + b = 0$ ，则w为超平面的法向量；样本点A(x)到超平面的距离为d,B(X0)为A在超平面上的投影。因为B(X0)在超平面上，所以有 $w^T x_0 + b = 0\tag{3.1.5}$ 由几何意义：($\frac{w}{||w||}$为单位向量,与d的乘积可以表示向量$\vec{BA}$)$$\vec{BA} = x - x_0 = d*\frac{w}{||w||}\tag{3.1.6} $$ 将（3.1.6）代入（3.1.5）， $$w^T (x - d*\frac{w}{||w||})+ b = 0\tag{3.1.7}$$ 化简可得，$$ d = \frac{|w^T x + b|}{|\frac{w^Tw}{||w||}|} = \frac{|w^T x + b|}{||w||} \tag{3.1.8} $$ 证毕。

（3）假设超平面（w,b）能够将样本正确分类，即对于任意训练样本$(x_i,y_i),y_i\in(-1,+1) $,有
\[y=\begin{cases} +1 & w^T x_i + b \geq +1\\ -1 & w^T x_i + b \leq -1 \end{cases} \tag{3.1.9}\]

则距离超平面最近的几个点，使（3.1.9）式中等号成立，这些点被称为“支持向量”（support vector），

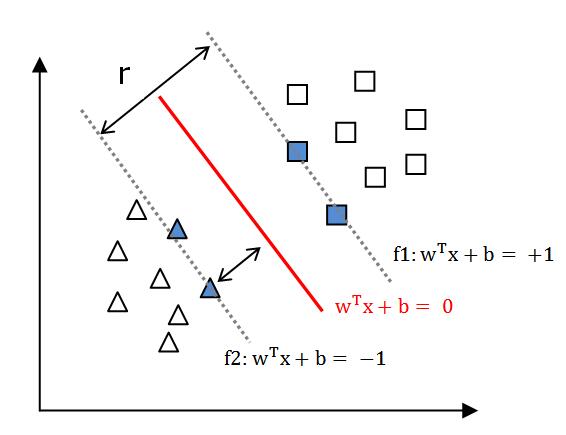
由式(3.1.4)和式(3.1.9)可知，\[ r = \frac{2}{||w||} \tag{3.1.10} \]
r被称为“间隔”（margin）。显然，当r越大时，超平面（w,b）的分类效果越好。
因此，寻找最优超平面等价于确定w,b,使得r最大，即 \[max_(w,b)\frac{2}{||w||} \\ s.t. y_i(w^T x_i + b) \geq +1 \tag{3.1.11} \]
为了便于计算，改问题可以等价为\[max_(w,b)\frac{1}{2}(||w||)^2 \\ s.t. y_i(w^T x_i + b) \geq +1 \tag{3.1.11} \]