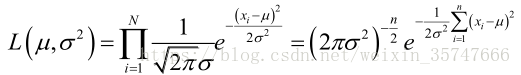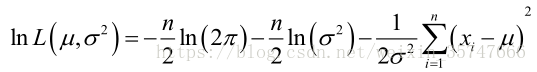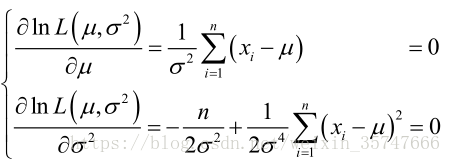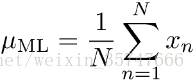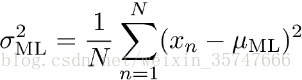模式识别与机器学习笔记（二）机器学习的基础理论

机器学习是一门对数学有很高要求的学科，在正式开始学习之前，我们需要掌握一定的数学理论，主要包括概率论、决策论、信息论。

一、极大似然估计（Maximam Likelihood Estimation，MLE ）

在了解极大似然估计之前，我们首先要明确什么是似然函数（likelihood function），对于 $p(x|θ)$，
当 $θ$是已知， $x$是变量， $p(x|θ)$表示概率函数，描述的是 $x$出现的概率是多少；
当 $x$是已知， $θ$是变量， $p(x|θ)$表示似然函数，描述的是对于不同的模型（ $θ$决定）出现样本点 $x$的概率是多少。
似然可以理解为概率，只是表征的含义不同，通常利用求极大似然来确定模型参数，极大似然的描述如下：
极大似然估计是一种已知样本，估计参数的方法。通过给定样本集 $D$估计假定模型的参数，极大似然估计可以帮助我们从参数空间中选择参数，使该参数下的模型产生 $D$的概率最大。

1.求解极大似然函数
重要前提：训练样本的分布能够代表样本的真实分布，每个样本集中的样本都是独立同分布的随机变量，并且有充分的训练样本。
已知样本集D={ $x_1,x_2,x_3,...,x_m$}，{ $y_1,y_2,y_3,...,y_m$}，则似然函数表示为
$L(θ)=p(y|x;θ)=\displaystyle\prod_{i=1}^{m} p(y^{(i)}|x^{(i)};θ)$，
确定 $θ$使模型出现样本集D的概率（表示为条件概率）最高即为我们所求，即
$θ=argmaxL(θ)=argmax\displaystyle\prod_{i=1}^{m} p(y^{(i)}|x^{(i)};θ)$，
为便于计算与分析，定义了对数似然函数 $H(θ)=logL(θ)$， $θ=argmax\displaystyle\sum_{i=1}^{m}logp(y^{(i)}|x^{(i)};θ)$，现在我们确定了目标函数 $H(θ)$，需要求得一组 $θ$使 $H(θ)$最大，可以通过求导数的方法解决这个问题，以高斯分布的参数估计（Gaussian Parameter Estimation）为例，求解过程如下，
设样本服从正态分布 $N(μ,σ^2)$，首先写出似然函数 $L(μ,σ^2)=p(x;μ,σ^2)=\displaystyle\prod_{n=1}^{N}N(x_n;μ,σ^2)$

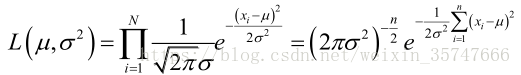
$L(μ,σ^2)$的对数为：

求导，得方程组：

解得：

       

2.误差平方和的解释
在模式识别与机器学习（一）中我们讲到采用误差平方和原理来求解多项式系数，为何使用误差平方和作为衡量模型精度的标准呢？用极大似然估计可以解释。
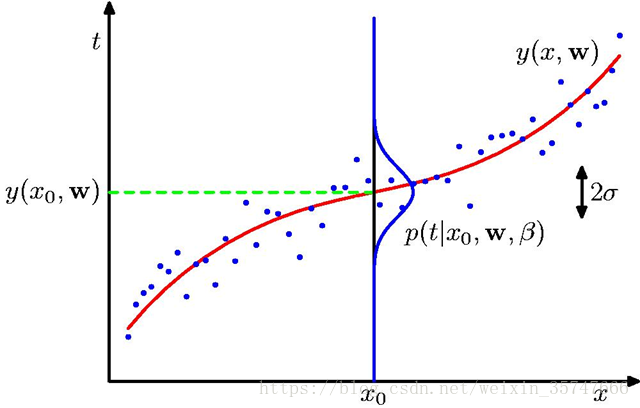
我们观察下图，这是上一节课中讲到的多项式曲线拟合模型，红色曲线代表拟合结果，蓝色点代表样本点。

我们把每一个 $x$看作独立的随机变量，对应的样本点 $t$服从均值为 $y(x_0,w)$的正态分布（一般来讲，误差服从均值为零的正态分布，平移 $y(x_0,w)$个单位），即 $p(t|x_0,w,β)=N(t|y(x_0,w),β^{-1})$，利用极大似然估计，使 $t$出现的概率最大， $p(t|x,w,β)=\displaystyle\prod_{n=1}^{N}N(t_n|y(x_n,w),β^{-1})$， $\ln p(t|x,w,β)=-\frac{β}{2}\displaystyle\sum_{n=1}^{N}\{y(x_n,w)-t_n\}^2+\frac{N}{2}\lnβ-\frac{N}{2}\ln(2π)$，观察此式，我们想要求得此式的极大值，则需使 $\frac{1}{2}\displaystyle\sum_{n=1}^{N}\{y(x_n,w)-t_n\}^2$取得最小值，得证。

极大似然估计是三种机器学习方法中最基础的一种，其余两种分别是贝叶斯估计方法和贝叶斯学习方法，极大似然估计和贝叶斯估计的计算结果是精确的参数值，而贝叶斯学习的计算结果是概率区间，在后边我们会单独一章细致地进行学习，这三种方法是机器学习的主线，掌握这三种方法的原理才能对后边各种模型的学习和理解游刃有余。

3.贝叶斯估计（最大后验概率，MAP）
我们需要知道，使用极大似然估计方法容易使模型产生过拟合，在上一章中我们解决的办法是增加正则项，并且证明了正则项有效地解决了过拟合问题。现在我们尝试从贝叶斯估计的角度推导出正则项的由来与合理性。

由贝叶斯公式我们得知， $posterior∝likelihood×prior$，即后验概率可由似然与先验概率相乘得到，之前讲到的极大似然估计，我们仅仅用到了 $likelihood$，现在我们假设参数有一个先验概率，如此便可通过公式求得后验概率，接下来与极大似然类似的，使后验概率最大，求得模型参数。
假定对参数 $w$，先验概率为 $p(w|α)=N(w|0,α^{-1}I)=(\frac{α}{2π})^{(M+1)/2}exp\{-\frac{α}{2}w^Tw\}$,
根据贝叶斯公式，求得后验概率 $p(w|x,t,α,β)∝p(t|x,w,β)×p(w|α)$，将似然函数与先验概率带入式中得到后验概率的数学表达式。欲使后验概率获得最大值，等价于 $βE(w)=\frac{β}{2}\displaystyle\sum_{n=1}^{N}\{y(x_n,w)-t_n\}^2+\frac{α}{2}w^Tw$取得最小值，我们发现，表达式中 $\frac{α}{2}w^Tw$即为前述的正则项，得证。
极大似然估计易导致过拟合，贝叶斯估计为参数提供了先验概率，形式上增加了正则函数，结果上抑制了过拟合的产生。

二、概率论基础（Probability Theory）

1. $p(X)=\displaystyle\sum_Yp(X,Y)$          $p(X,Y)=p(Y|X)p(X)$
2.贝叶斯理论（Bayes’Theorem）
$p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)}$           $posterior∝likelihood×prior$
3.概率函数
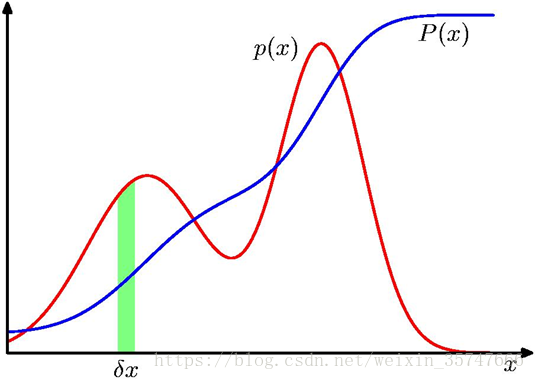
累积分布函数：描述随机变量取值分布规律的数学表示，表示对于任何实数 $x$，事件 $X<x$的概率。
概率密度函数：描述随机变量的输出值，在某个确定的取值点附近的可能性的函数。随机变量的取值落在某个区域之内的概率为概率密度函数在这个区域上的积分。当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。概率密度函数表示的是概率的分布情况，在某个点取值高说明样本在该点附近出现的概率大。

$p(x)$表示概率密度函数， $P(x)$表示概率分布函数。
$p(x∈(a,b))=\int_a^bp(x)dx$            $p(x)≥0$            $\int_{-∞}^{∞}p(x)dx=1$            $P(z)=\int_{-∞}^{z}p(x)dx$

数学期望：试验中每次可能结果的概率乘以其结果的总和，数学期望可以理解为均值。
$E[f]=\displaystyle\sum_xp(x)f(x)$            $E[f]=\int p(x)f(x)dx$
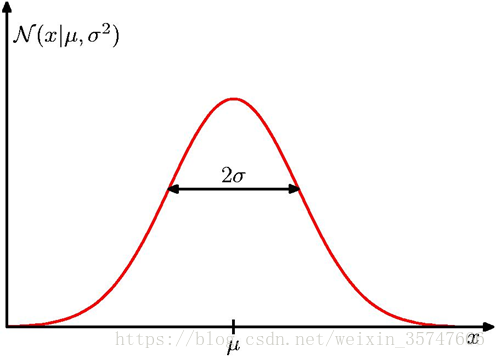
4.高斯分布（Gaussian Distribution）
若随机变量X服从一个数学期望为 $μ$、标准方差为 $σ^2$的高斯分布，记为： $X$~ $N(μ,σ^2)$，概率密度如下图所示，

$N(x|μ,σ^2)=\frac{1}{(2πσ^2)^{1/2}}exp\{-\frac{1}{2σ^2}(x-μ)^2\}$            $N(x|μ,σ^2)>0$            $\int_{-∞}^{∞}N(x|μ,σ^2)dx=1$
$E[x]=\int_{-∞}^{∞}N(x|μ,σ^2)xdx=μ$            $E[x^2]=\int_{-∞}^{∞}N(x|μ,σ^2)x^2dx=μ^2+σ^2$
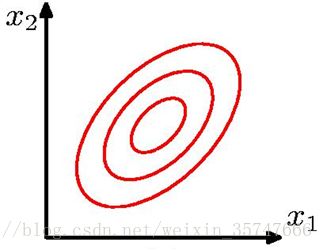
二元高斯分布如下图所示，

三、信息熵（Entropy）

信息熵在编码学、统计学、物理学、机器学习中有很重要的应用，我们有必要对信息熵的相关知识具备一定程度的了解。

1.信息量
信息量用一个信息的编码长度来定义，一个信息的编码长度与其出现概率是呈负相关的，可以理解为为使总信息编码量最低，出现高概率的的信息编码长度应相对短，也就是说，一个词出现的越频繁,则其编码方式也就越短。信息量计算方法为，
$I=\log_2(\frac{1}{p(x)})=-\log_2(p(x))$

2.信息熵
信息熵代表一个分布的信息量（信息量的均值），或者编码的平均长度，
$H(p)=\displaystyle\sum_xp(x)\log_2(\frac{1}{p(x)})=-\displaystyle\sum_xp(x)\log_2(p(x))$
从数学公式中可以看出，信息熵实际上是一个随机变量的信息量的数学期望，那么信息熵的含义是什么呢？信息熵是系统有序化程度的度量，系统越有序，信息熵越低，也就是说，系统中各种随机性的概率越均等，不确定性越高，信息熵越大，反之越小。为什么有这种对应关系呢？我们假设系统有两个事件 $A$和 $B$，当 $P(A)=P(B)=\frac{1}{2}$时，我们无法判断会发生事件 $A$还是 $B$，这时系统的不确定性高、系统无序；当 $P(A)=\frac{99}{100}$， $P(B)=\frac{1}{100}$，此时大概率发生事件 $A$，系统具有一定的确定性、相对有序。前者信息熵高，后者信息熵低。
接下来我们举一个信息熵计算的例子，如下所示，

$H(p)=-\frac{1}{2}\log_2\frac{1}{2}-\frac{1}{4}\log_2\frac{1}{4}-\frac{1}{8}\log_2\frac{1}{8}-\frac{1}{16}\log_2\frac{1}{16}-\frac{4}{64}\log_2\frac{1}{64}=2bits$

$average$ $code$ $length$ $=\frac{1}{2}×1+\frac{1}{4}×2+\frac{1}{8}×3+\frac{1}{16}×4+4×\frac{1}{16}×6=2bits$
信息熵代表编码的平均长度。

3.相对熵（KL散度）
相对熵又称KL散度，对于同一个随机变量 $x$有两个单独的概率分布 $p(x)$和 $q(x)$，我们可以用KL散度(Kullback-Leibler Divergence)来衡量这两个分布的差异。在机器学习中，P表示样本的真实分布，Q表示模型预测的分布。
KL散度的计算公式为： $p$对 $q$的相对熵 $D_{KL}(p||q)=\displaystyle\sum_{i=1}^{n}p(x_i)\log(\frac{p(x_i)}{q(x_i)})$， $D_{KL}$的值越小，表示 $q$分布和 $p$分布越接近。

4.交叉熵（cross-entropy）
$D_{KL}$可以变形得到 $D_{KL}=\displaystyle\sum_{i=1}^np(x_i)\log p(x_i)-\displaystyle\sum_{i=1}^np(x_i)\log q(x_i)=-H(p(x))+[-\displaystyle\sum_{i=1}^np(x_i)\log q(x_i)]$，等式的前一部分是 $p$的信息熵，等式的后一部分就是交叉熵，
$H(p,q)=-\displaystyle\sum_{i=1}^np(x_i)\log q(x_i)$。在机器学习中，需要评估 $label$和 $predict$之间的差距，应使用相对熵来衡量，由于 $D_{KL}$的前一部分不变，所以在优化过程中，只需关注交叉熵即可，因此在机器学习中常常用交叉熵作为 $loss$来评估模型。

未完待续