文本上的算法读书笔记二--我们生活在一个寻求最优的世界里

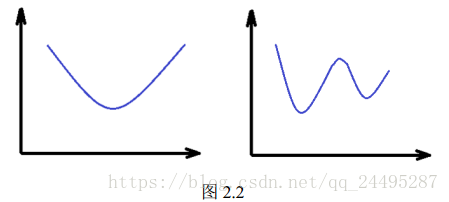
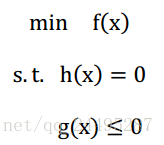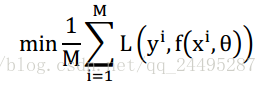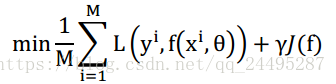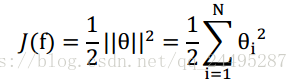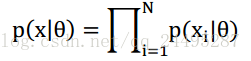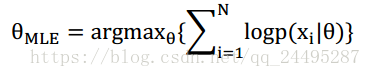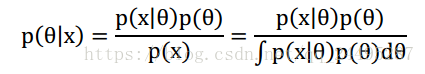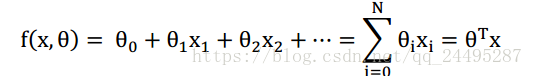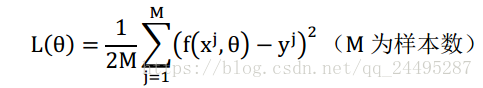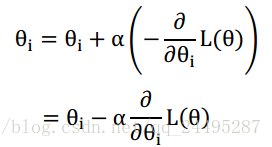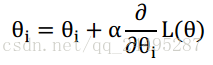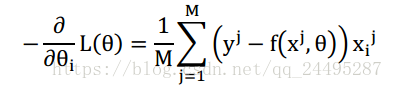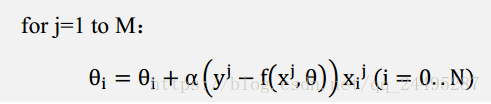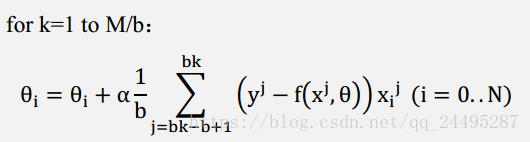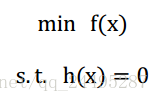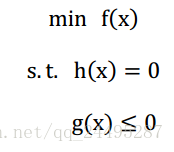最优化模型是机器学习的内功，几乎每一个机器学习背后都是一个最优化模型。

2.1 最优化问题

科学抽象于生活，科学服务于生活。每个机器学习背后都是个最优化问题。希望付出最小的成本来获得最大的收益。

一般的最优化形式表示如下：

是目标函数，和分别是约束条件，没有约束条件的（只有,称为无约束优化，只有和称为等式约束优化，和、都有称为不等式约束优化）

设计一个模型来代替真实模型（假设为你设计的模型，为真实模型，为整个模型的输入），怎么才能说你设计的模型很好呢？只要你设计的模型与真实的模型误差很小，那么说明你的模型越好，误差通常使用损失函数来表示，常用的有：

平方误差：

绝对损失：

合页损失：

似然损失：

似然损失的最小就是，的最大化。

损失函数的期望，称为期望风险，学习的目标是使期望风险最小，

期望风险是指你设计的模型和真实模型的期望误差，虽然不知道真实模型是什么，但是可以用（x,y）的输入对，用计算好的

直接替代真实模型就可以了，这种方法计算出来的风险就是经验风险。根据大数定力，样本对趋于无穷大，经验风险也就是越接近期望风险。

经验风险最小化，如果样本有限，产生过拟合现象。过拟合现象就是把数据拟合的太完美，模型复杂度高，然而到未知数据中拟合的很差（对未知数据的预测能力叫做泛化能力）。欠拟合就是在样本数据上拟合的不好，在未知数据上也不好。为了避免过拟合现象，就要对模型的复杂度进行惩罚，这就是正则化。

结构风险最小化。

正则化公式：

范数，范数，范数

最终的结果，如何确定一个好的模型呢？

需要交叉验证

交叉验证：

随机的把样本分为：训练集，验证集

首先在训练集中训练各种模型然后在验证集上评价各个模型的误差，选出一个误差最小的模型就是好的模型。

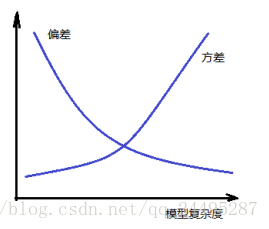
偏差：

衡量单个模型的误差，比如这个模型的偏差来表示，这个模型的偏差可以用来表示。所以偏差是衡量单个模型自身的好坏，而不管别的模型怎么样。

方差：

方差是多个模型间比较，并不管自己的这个模型和真实模型的误差多大，而是从别的模型来衡量自己的好坏，也就是认为所有模型的平均值，就可以代表真实模型。

（潜在假设是大多数情况是正常无噪声的，否则代表不了真实模型）

比如这个模型的方差可以用来表示

模型越复杂，偏差越小，方差就越大

模型越简单，偏差越大，方差就越小，博弈的过程，最好的模型就是偏差和方差之和最优的模型。

根据交叉验证选个最好的模型。

2.2 最大似然估计/最大后验估计

选模型，比如：线性模型，高斯模型等。这些公式只需根据数据带入公式就可以求解,这就是参数估计，如果对一无所知的模型估计参数，那就是非参数估计。

最大似然估计和贝叶斯代表了频率派和贝叶斯派的观点。

频率派是参数是客观存在的，只是未知而已，频率派关系最大似然函数，观察的变量是x,x的分布函数是，那么最大似然函数就是的估计值，它使得事件发生的可能性最大，即：

通常认为x是独立同分布的，

有

由于连乘会造成浮点下溢，通常最大化对数形式，就是：

拟合样本数据好，不见得拟合未知数据就很好，所以频率派认为我没见过飞机相撞，那么飞机就不可能相撞。

贝叶斯说了，参数也应该是随机变量，和一般随机变量没有本质区别，也有概率。没见过飞机相撞，飞机还是有概率相撞，正是因为参数不能固定，当输入一个x，不能用确定的Y表示结果，必须用概率的方式表达出来。希望得到所有在获得观察数据x后的分布情况，就是后验概率，有：

积分其实就是所有的后验概率的汇总，其实是与最优无关的，采用近似的方法求后验概率，这就是最大后验估计：

最大似然估计其实是经验风险最小化的一个例子，而最大后验估计是结构风险最小化的一个例子。

如果样本足够大，最大后验概率和最大似然估计趋向于一致，如果样本数量为0，最大后验就仅由先验概率决定，就像推荐系统中对于毫无历史数据的用户，只能推热门的内容。进入最大后验估计看着要比最大似然估计完善，但是最大似然估计简单，很多方法还是使用最大似然估计。

最小二乘估计：

估计值和观测值之差的平方和最小。最小二乘有个假设，模型服从高斯分布。

2.3 梯度下降法

求解最优化问题，本质上就是怎么向最优解移动，达到某个条件就停止。

导数为0。有的最优化问题没有解析解，只能通过一些启发式算法（遗传算法等）或者数值计算的方法来求解。对于无约束优化问题常用的算法有：梯度下降法，牛顿法/拟牛顿法，共轭梯度法，坐标下降法等

对于有约束问题大多是通过拉格朗日乘子法转换成无约束问题来求解。

线性回归模型来看梯度下降法：

线性函数：

损失函数使用平方损失函数，则有：

梯度下降法指出，函数f在某点x沿着梯度相反的方向下降最快。

其中是个定值，就是学习速度，控制每步移动的幅度。

相反，如果是损失函数最大化，就是梯度上升法：

又有：

这就是梯度下降的迭代流程，首先选定一个然后使用公式迭代，一直到收敛停止，就解出了参数

公式中有个求和，也就是每次迭代都需要计算全部的样本，当样本M很大时，计算代价很大，需要相关好的办法减少计算，这就是随机梯度下降法（SGD）.

可以并行计算，因为样本间是无关的。介于梯度下降和随机梯度下降之间的办法，是批梯度下降，思想是使用b个样本来更新梯度，流程如下：

等式约束优化问题：

写出它的拉格朗日乘子法：

用分别对求导数，然后令导数为零，就可以解出求导数，然后令导数为0，可以解出的候选最优解了。

不等式约束优化问题：

写出它的拉格朗日乘子法：

要想有和原不等式约束化问题一样的最优解，必须满足KKT条件：

1.分别对x求导为0

2.

3.

4.

5.

当原问题不好求解的时候，可以利用拉格朗日乘数法得到其对偶问题，满足强对偶性条件时它们的解是一致的。

定义一个函数：

这个函数是的函数，如果x违反原始问题的约束条件，即或者，那么总是可以调整和来使得有最大值为正无穷，而只有都满足约束时，为，也就是说的取值是：或者，所以，就是求了。即：

再定义一个函数：，则有：

和互为对偶问题。可以证明：，如果满足强对偶性，目标函数和所有不等式约束函数都是凸函数，等式约束是仿射函数（），且所有不等式约束都是严格的约束，那么，那么原问题和对偶问题一致。

如果不好求解，可以用求解。

最优化问题很简单：首先要有一个模型：目标函数和约束函数，不同的问题会对应不同的模型，需要自己设计，然后对模型的参数进行求解。