题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 nn 个深埋在地下的宝藏屋, 也给出了这 nn 个宝藏屋之间可供开发的mm 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。
新开发一条道路的代价是:
\mathrm{L} \times \mathrm{K}L×K
L代表这条道路的长度,K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代 价最小,并输出这个最小值。
输入输出格式
输入格式:
第一行两个用空格分离的正整数 n,mn,m,代表宝藏屋的个数和道路数。
接下来 mm 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏 屋的编号(编号为 1-n1−n),和这条道路的长度 vv。
输出格式:
一个正整数,表示最小的总代价。
输入输出样例
输入样例#1: 复制
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
输出样例#1: 复制
4输入样例#2: 复制
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 2 输出样例#2: 复制
5说明
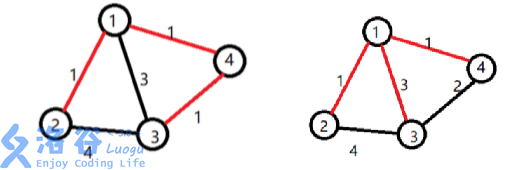
【样例解释1】
小明选定让赞助商打通了11 号宝藏屋。小明开发了道路 1 \to 21→2,挖掘了 22 号宝 藏。开发了道路 1 \to 41→4,挖掘了 44号宝藏。还开发了道路 4 \to 34→3,挖掘了33号宝 藏。工程总代价为:1 \times 1 + 1 \times 1 + 1 \times 2 = 41×1+1×1+1×2=4
【样例解释2】
小明选定让赞助商打通了11 号宝藏屋。小明开发了道路 1 \to 21→2,挖掘了 22 号宝 藏。开发了道路 1 \to 31→3,挖掘了 33号宝藏。还开发了道路 1 \to 41→4,挖掘了44号宝 藏。工程总代价为:1 \times 1 + 3 \times 1 + 1 \times 1 = 51×1+3×1+1×1=5
【数据规模与约定】
对于20\%20%的数据: 保证输入是一棵树,1 \le n \le 81≤n≤8,v \le 5000v≤5000 且所有的 vv都相等。
对于 40\%40%的数据: 1 \le n \le 81≤n≤8,0 \le m \le 10000≤m≤1000,v \le 5000v≤5000 且所有的vv都相等。
对于70\%70%的数据: 1 \le n \le 81≤n≤8,0 \le m \le 10000≤m≤1000,v \le 5000v≤5000
对于100\%100%的数据: 1 \le n \le 121≤n≤12,0 \le m \le 10000≤m≤1000,v \le 500000v≤500000
解法一:随机化贪心,用类似prim的算法每次选伪最优解扩展。
#include<bits/stdc++.h>
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=15,MAXM=1005,INF=1e9;
struct Edge{
int v,w,nxt;
}e[MAXM<<1];
int dep[MAXN],dis[MAXN][MAXN];
struct Node{
int u,v,d;
bool operator < (const Node& tmp)const{
return d>tmp.d;
}
};
int h[MAXN],tot;
int n,m,vis[MAXN];
inline void add(int u,int v,int w)
{
e[tot]=(Edge){v,w,h[u]};
h[u]=tot++;
}
namespace task1{
int rt,ans=1000;
int size[MAXN];
void dfs1(int u,int fa)
{
int i,max_size=0;
size[u]=1;
for(i=h[u];~i;i=e[i].nxt){
int v=e[i].v;
if(v==fa) continue;
dfs1(v,u);
size[u]+=size[v];
max_size=max(max_size,size[v]);
}
max_size=max(max_size,n-size[u]);
if(max_size<ans){
ans=max_size;
rt=u;
}
}
void dfs2(int u,int fa,int dep)
{
int i;
for(i=h[u];~i;i=e[i].nxt){
int v=e[i].v,w=e[i].w;
if(v==fa) continue;
ans+=w*dep;
dfs2(v,u,dep+1);
}
}
int main()
{
int i,j;
dfs1(1,-1);
ans=0;
dfs2(rt,-1,1);
cout<<ans<<endl;
return 0;
}
}
namespace task2{
int main()
{
int u,i,j,k,tmp,ans=INF;
f(k,1,n){
f(i,1,n){
f(j,1,n){
if(dis[i][k]>INF||dis[j][k]>INF) continue;
dis[i][j]=dis[j][i]=min(dis[i][j],dis[i][k]+dis[j][k]);
}
}
}
f(i,1,n){
tmp=0;
f(j,1,n){
tmp+=dis[i][j];
}
ans=min(ans,tmp);
}
cout<<ans<<endl;
return 0;
}
}
int prim(int x)
{
int i,j;
memset(vis,0,sizeof(vis));
int res=0;
priority_queue<Node> q;
queue<Node> p;
q.push((Node){0,x,0});
f(i,1,n){
int u=q.top().v;
Node tmp=q.top();
q.pop();
while(!q.empty()&&(vis[u]||rand()%(n)<1)){
if(!vis[u]) p.push(tmp);
u=q.top().v;
tmp=q.top();
q.pop();
}
vis[u]=1;
res+=tmp.d;
while(!p.empty()){
q.push(p.front());
p.pop();
}
dep[u]=dep[tmp.u]+1;
f(j,1,n){
if(vis[j]||j==u||dis[u][j]>INF) continue;
q.push((Node){u,j,dep[u]*dis[u][j]});
}
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
srand(time(NULL));
memset(h,-1,sizeof(h));
int i,j,u,v,w;
int pd,flag=1,ans=INF;
cin>>n>>m;
f(i,1,m){
cin>>u>>v>>w;
add(u,v,w);
add(v,u,w);
if(i==1) pd=w;
else if(w!=pd) flag=0;
}
if(m==n-1){
task1::main();
return 0;
}
memset(dis,60,sizeof(dis));
f(u,1,n){
dis[u][u]=0;
for(i=h[u];~i;i=e[i].nxt){
int v=e[i].v,w=e[i].w;
dis[u][v]=dis[v][u]=min(dis[u][v],w);
}
}
if(flag){
task2::main();
return 0;
}
int T=600;
while(T--){
f(i,1,n){
ans=min(ans,prim(i));
}
}
cout<<ans<<endl;
return 0;
}
解法二:状压dp。f[s]表示状态为s时的最小花费,转移时枚举i,j,从i往j建路,并记录深度dep[j]=dep[i]+1。
#include<bits/stdc++.h>
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=15,INF=1e9;
int a[MAXN][MAXN];
int n,m;
int f[1<<12],dep[MAXN];
void dfs(int sta)
{
int i,j;
f(i,0,n-1){
if((sta&(1<<i))==0) continue;
f(j,0,n-1){
if(j==i||dep[j+1]||(sta&(1<<j))||a[i+1][j+1]>=INF) continue;
if(f[sta|(1<<j)]>f[sta]+a[i+1][j+1]*dep[i+1]){
f[sta|(1<<j)]=f[sta]+a[i+1][j+1]*dep[i+1];
dep[j+1]=dep[i+1]+1;
dfs(sta|(1<<j));
dep[j+1]=0;;
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
memset(a,60,sizeof(a));
int i,j,u,v,w;
int ans=INF;
cin>>n>>m;
f(i,1,m){
cin>>u>>v>>w;
a[u][v]=a[v][u]=min(a[u][v],w);
}
f(i,0,n-1){
memset(f,60,sizeof(f));
memset(dep,0,sizeof(dep));
f[1<<i]=0;
dep[i+1]=1;
dfs(1<<i);
ans=min(ans,f[(1<<n)-1]);
}
cout<<ans<<endl;
return 0;
}
解法三:状压dp。

那么,我们可以考虑这样子设状态:
设f[i][j]表示到第i层,总共取了的点的状态为j。
这样的话,转移就可以取出来了:
f[i][j]=MIN(f[i-1][k]+trans[k][j]*(i-1))f[i][j]=MIN(f[i−1][k]+trans[k][j]∗(i−1))
(k为j的子集,即有可能转移到j的状态) (trans[k][j]表示从状态k转移到状态j的最小花费的路程)
trans需要暴力预处理出来。
怎么枚举子集呢?
如果2^n枚举就会T掉,因为我们枚举到了非子集的情况。
这里就引出了枚举子集的小技巧
对于状态x,它的子集为:p=x,p!=0,p=(p-1)&x (至于怎么证明,这里就不给出了,在草稿上推一推就会发现里面的精妙了)
答案就是min(f[i][2^n-1]),初始化f[1][2^(i-1)]=0 (i∈[1,n])
.
#include<bits/stdc++.h>
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=13,INF=1e9;
int n,m;
int a[MAXN][MAXN];
int f[1<<12][1<<12],g[1<<12][1<<12];
int main()
{
ios::sync_with_stdio(false);
memset(a,60,sizeof(a));
memset(g,60,sizeof(g));
int i,j,k,u,v,w;
int ans=INF;
cin>>n>>m;
f(i,1,m){
cin>>u>>v>>w;
a[u][v]=a[v][u]=min(a[u][v],w);
}
int ALL=(1<<n)-1;
f(i,1,ALL){
for(j=(i-1)&i;j;j=(j-1)&i){ //j是i的真子集
int s=i^j; //s为i-j。
int pos=log2(s&(-s));
w=INF;
f(k,1,n){
if(j&(1<<(k-1))){
w=min(w,a[pos+1][k]);
}
}
if(w==INF){
f[j][i]=INF;
continue;
}
f[j][i]=f[j][i^(s&(-s))]+w;
}
}
f(i,1,n){
g[0][1<<(i-1)]=0;
}
f(i,1,n-1){
f(j,1,ALL){
for(k=(j-1)&j;k;k=(k-1)&j){
if(f[k][j]>=INF) continue;
g[i][j]=min(g[i][j],g[i-1][k]+i*f[k][j]);
}
}
}
f(i,0,n-1){
ans=min(ans,g[i][ALL]);
}
cout<<ans<<endl;
return 0;
}