Part IV Generative Learning Algorithms

回顾上一部分的内容，我们解决问题的出发点在于直接对p(y|x; $\small \theta$ )建模：如线性回归中y建模为高斯分布，逻辑回归y建模为伯努利分布。这样建模的好处在于可以直接得到x到y的映射关系，理解起来也比较直接。这样建模的算法，称为判别学习算法（discriminative learning algorithms）。除此之外，有另外一种建模的思路，即生成学习方法（generative learning algorithms）的思路，并不是直接对于p(y|x; $\small \theta$ )建模，而是对于p（y）和p（x|y）进行建模，当做先验知识，然后利用贝叶斯公式进行后验概率p（y|x）的推导。根据贝叶斯公式，对每一类都进行计算，选取后验概率最大的一类作为数据的类别。

（1）

假设在二分类问题中，虽然p（x）可以通过得到：

$\small p(x) = p(x|y=0)*p(y=0) + p(x|y=1)*p(y=1)$

但是一般都不关注于p(x)，因为对于每一类来说，p（x）都是一样的：

单看上面可以不会很明白，让我们看看两种常用的生成学习算法，会加深我们的理解。

高斯判别分析（Gaussian Discriminant Analysis，GDA）

高斯判别分析（GDA）常用作当x服从于高斯分布时（也就是连续性变量）的建模。虽然叫做高斯判别分析，但是却是一个生成算法。利用二分类问题作为介绍的背景，GDA流程如下。

假设y服从于伯努利分布，x|y分别服从于二元高斯分布。

写出上式分布的表达式：

（2）

通过这样建模，参数有 $\small \phi$ ， $\small \mu _{0}$ ， $\mu _{1}$ ，协方差阵 $\Sigma$ ，共四个参数。这里两个二元高斯分布采用同样的 $\Sigma$ ，这是需要重点注意的地方，至于为什么要这样做，我也没有搞明白，有可能是为了简单接下来的参数计算的步骤吧，或许也有更深层次的原因。

进行极大似然估计：

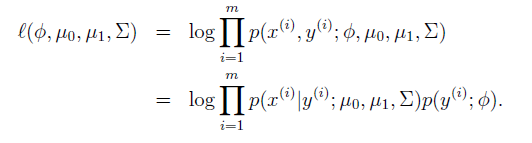
直接求解得到参数：

$\phi$ ：正样本所占的比例。

$\small \mu _{0}$ ：负样本特征向量的均值。

$\mu _{1}$ ：正样本特征向量的均值。

$\Sigma$ ：所有样本计算得到的协方差阵。

有了以上参数，那么（2）式就得到了。当有新的待判断的数据来临时。将该数据分别代入（1）式，计算结果，看属于哪一类的概率大，就归入哪一类。至此，模型就建立好了。

讲义中，有一张图，可以帮助理解GDA在做了什么。

分别以正样本的均值和负样本的均值，生成相同协方差的二元高斯函数，虽然在判断样本属于哪一类时，需要带入贝叶斯公式进行计算，但是本质正如上图所示，画出一条直线，直线上方属于一类而下方属于另一类。在此情形下，不就和逻辑回归、感知机算法那样一刀切判别样本如出一辙吗？都是需要一条直线作为决策边界进行决断。看来判别学习算法逻辑回归和生成学习算法GDA仿佛又有某种联系。

高斯判别分析和逻辑回归的思考

那么高斯判别分析（GDA）和逻辑回归（LR）二者是否有某种共性呢？果不其然，你可以接着（2）式往下推（有推出来的伙伴不吝赐教），看看GDA中的后验概率p（y=1|x）应该是怎么样：

根据先验分布推断出来的后验分布p（y=1|x）正是逻辑回归。这种感觉的确很奇妙。

在GDA中，若先验概率p（x|y）服从于多元正态分布且采用相同的 $\Sigma$ 作为参数，那么可以得到其后验概率的形式即为逻辑回归。但是反之却不是这样。后验概率为逻辑回归有可能对应着其他的分布：例如将上述的先验分布改为参数为 $\lambda _{0}$ 和 $\lambda _{1}$ 的泊松分布，那么得到的后验概率形式也仍然为逻辑回归形式。

换句话说，GDA是比LR更为强的假设。因为由GDA可以推出LR，单LR却不一定保证GDA。

因为GDA的假设更强，所以如果x对于高斯分布拟合的越好，那么GDA的效果也就越好，因此往往GDA不太需要许多的数据去拟合数据真实的分布特征，就能够得到较好的效果；而反观如果从判别学习算法LR出发，由于作为相对较弱的假设，因此对于数据的包容性也就越好，模型的鲁棒性也较强，能够适应于其他分布的数据，因此也往往需要更多的数据去拟合。这二者的互相权衡，也为我们选择那种算法提供了一些参考的地方。一些关于生成学习算法和判别学习算法的讨论在下文也会涉及。

朴素贝叶斯（Naive Bayes，NB）

上文提到的GDA解决的是连续性变量的问题，那么如果变量为离散型呢？这里可以采用朴素贝叶斯的方法进行解决。

以垃圾邮件分类问题作为例子。又是一个二元分类的问题。但是与之前的不同，根据对于特征向量的建模方式，NB算法可以有两种形式。

多元伯努利事件模型

在多元伯努利事件模型中，我们这么设置特征向量x，这种思路也是最基本的思路：

x的长度即为词字典的长度，若字典有50000个单词，x即为50000维向量，很明显便会发现这个向量很稀疏，这样设置很占内存空间。不禁会感到向量维数感觉有点多啊，一个修改办法便是，你可以选用你的训练集中所出现过的词组成你的字典，这样会减少一些维数。通过上述方式设置特征向量，也就是说一封邮件用一个n维向量（n为字典中词的个数）表示，若邮件中出现某单词，那么该位置上就取值为1，否则为0。这样看来一封邮件就是一个n元伯努利分布变量组成的向量啊。

下面，便要开始建模了。按照生成学习算法的思路，首先，我们应该给p（x|y）建模，为了建模，这里需要做一个强假设：假设x中的每个元素 $x_{i}$ 互相条件独立。这个假设的设置，也是朴素贝叶斯算法这个名称的由来（真是朴素）。

注意这里条件独立与独立的区别：独立则条件独立，反之则不一定对，条件独立这个假设相对于独立这个假设要弱一些：

若A，B独立，则 p（AB）=p（A）p（B）

若A，B条件独立，则 p（AB|C）=p（A|C）p（B|C）

在朴素贝叶斯假设（Naive Bayes Assumption）的基础上，首先给p（x|y）建模：

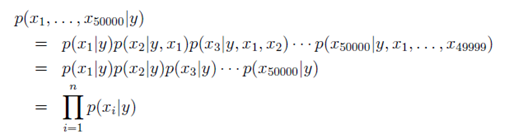
第一个等式由链式法则直接推出；第二个等式基于朴素贝叶斯假设推出，因为互相条件独立，彼此不受影响。

对于垃圾邮件分类来说，其是一个伯努利分布；而对于每一个 $x_{i}$ 来说，又满足一个伯努利分布。因此我们需要求解的参数如下所示。共计 1 + 2 * v 个参数，这里 v 表示字典中单词的个数。

构建最大似然方程：

求解参数：

$\phi _{j|y=1}$ ：在垃圾邮件中，j单词出现的频率。

$\phi _{j|y=0}$ ：在非垃圾邮件中，j单词出现的频率。

$\phi _{y}$ ：垃圾邮件占整个邮件的比例。

得到参数后，当有一封邮件来临需要判断是否为垃圾邮件时，首先构造该邮件的特征向量，然后分别计算后验概率 p（y=1|x）和p（y=0|x）进行判断，选取概率最大的一类进行归类（0或1）就可以了。例如计算p（y=1|x），可根据下式进行计算。因为比较的时候分母是相同的，所以实际计算的时候，只计算分子就可以了。

这就是最朴素的贝叶斯分类的原理了，思路清晰，模型不复杂，虽然做了一个较强的假设，但是仍然能够得到不错的分类效果。

同样也可以对于其做一些扩展：例如 $x_{i}$ 的取值可以从（0,1）扩展为（0,1,2...k），其实就是从伯努利分布扩展为多项分布。道理是一样的，这里就不进行推导了。

记得在上文提到，这样构造特征向量感觉有点笨，那么可以在构造特征向量这里出发，引出下面一种建模方式。

多项式事件模型

让我们再看一下第一种特征向量的表示方式：字典有多少个单词，那么特征向量就有多少维，这实际上是一个很稀疏的特征向量。那么另外一种表现形式，就是从邮件本身的角度出发进行建模，假设邮件由125个单词组成：

那么这里的每个 $x_{i}$ 的取值不再为0或者1，而是为该单词在字典中的序号，若字典中有v个单词，那么 $x_{i}$ 的取值为（1,2,3...v）。也就是说现在的 $x_{i}$ 不再是伯努利分布了，而是多项式分布。这样做的话就可以起到大大缩小每个特征向量的目的，但是应注意由于邮件长度不同，因此每封邮件的特征向量维度也不同。

同样应用朴素贝叶斯假设进行p（x|y）建模：

形式上与之前一致，但是注意几个细节。这里的n表示邮件的长度而不是字典的长度；这里的 $x_{j}$ 取值有v个（v=字典中单词的数量），且 $x_{j}$ 服从于多项分布而不是伯努利分布。

需要计算的参数以下，参数数量同样为 1 + 2*v：

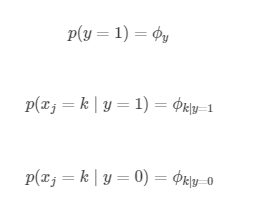
构建似然函数：

进行参数估计得到结果：

$\phi _{k|y=1}$ ：垃圾邮件中单词k出现次数除以垃圾邮件中单词总数。

$\phi _{k|y=0}$ ：非垃圾邮件中单词k出现次数除以非垃圾邮件中单词总数。

$\phi _{y}$ ：垃圾邮件数量除以总邮件数量。

对比多元伯努利事件模型和多项式事件模型，可以发现二者求解的参数一样多，若字典长度为v，那么都求解了2*v+1个参数。但是这里仍然会存在着一些不同。因为在实际中，邮件的长度总是小于字典的长度，甚至于远远小于字典长度，这就造成了二者的不同。

其中最明显的一点在于，多项式事件模型与多元伯努利事件模型的区别在于前者可以用较小的特征向量表示每封邮件，。

另外一点在于判断模型归属的计算之上。当获取模型参数建立模型后，在生成模型算法中，我们会通过分别计算后验概率来判断类别的归属。那么二者计算的差异就在于 $\prod p(x_{i}|y=1)$ 之上。在多元伯努利事件模型之中，需要计算v次连乘（v代表字典中单词个数），而多项式事件模型中则需要进行n（n代表邮件长度）次连乘。这就体现了计算差异，因为往往v和n不在于一个数量级，而且v远远大于n。虽然在多元伯努利事件模型之中，参数 $\phi$ 的计算要比多项式事件模型参数 $\phi$ 计算要稍微简单，但是考虑参数的值只计算了一次，所以参数的计算代价相比而言不会太高。因此，总体上来看，多项式事件模型节约了表示特征向量的内存，同时也减少了后验概率计算的时间。

拉普拉斯平滑（Laplace Smoothing）

我们可以对朴素贝叶斯算法做一个改进，从而增强其鲁棒性。这个改进称为拉普拉斯平滑。我们先看会在朴素贝叶斯算法中存在的一个问题。假设字典为50000维，有一个单词HAHA，在字典中的序号为35000，但是没有在你的训练集合中出现过，也就是说在用来训练的邮件中，不管是正样本还是负样本都没有出现过HAHA这个单词，那么在利用最大似然估计去计算参数时会显然得到如下结果：

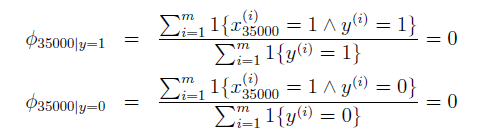
不管是对于垃圾邮件还是非垃圾邮件，参数都会被计算为0。那么这会带来什么问题呢？

假设现在，有一封邮件需要判断是否为垃圾邮件，且该邮件中含有HAHA这个单词。将该邮件带入后验概率公式进行判断：

ZeroDivisionError ：因为 $p(x_{35000}|y=1) = \phi _{35000|y=1} = 0$ ，且 $p(x_{35000}|y=0) = \phi _{35000|y=0} = 0$ 。因此对于连乘的计算，结果都为0。这时候，就无法进行判别了。

解决这个问题的方法也很简单，既然错误的原因是在训练数据中没有出现这个单词，那么让每个单词至少都出现，即给每一个初始的值赋予一个非0的值，就可以解决了。最直接的做法便是假设每个单词都至少出现了一次。以多项分布为例，假设 $\phi _{j}$ 的取值为（1,2,3...k）共k个可能。那么相应地修改参数表示：

其实这个操作可以理解为多增加了k个样本，且每个样本都只在第k的位置为1（以多元伯努利分布为例）。这样就使得每个单词都至少出现一次，因此分母为m+k，从而保证

$\sum_{j=1}^{k}\phi _{j}=1$

因此在多元伯努利事件模型中，修改参数为：

在多项事件模型中，修改参数为：

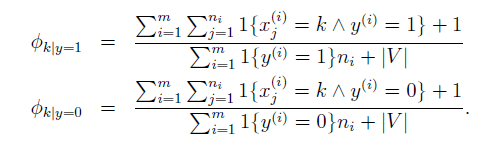
其中 $\left | V \right |$ 代表单词的数量。

小结

在此对于判别学习算法和生成学习算法的思路进行小结。

判别学习算法的思路在于，针对要解决的实际问题，根据先验知识，可以先对p（y）建模，例如线性回归中的高斯分布和逻辑回归中的伯努利分布；之后根据一些方式（如GLM）对于 $p(y|x;\theta )$ 进行建模，建模后根据极大似然估计的方式求解参数从而得到模型。这相当于直接建立了x到y的映射关系，因此当有新的数据时，直接通过模型就可以得到结果。

生成学习的思路在于，同样针对要解决的问题，根据先验知识，对于p（y）建模，例如GDA和NB中的伯努利分布；之后同样是根据先验知识，对 $p(x|y;\theta )$ 进行建模，同样是根据极大似然估计的方式求解参数从而得到模型，此时得到的是p（x|y）的模型，相当于得到先验概率；如果是分类问题，之后根据贝叶斯公式，推测出属于每一类的后验概率，根据得到的最高的后验概率判断数据属于哪一类。

就过程而言，感觉生成学习算法像是走了一条弯路，实际上我觉得生成学习算法走的是一条比判别学习算法更强假设的路：例如GDA中假设p（x|y）每一类服从高斯分类且协方差阵相同；NB中假设各个 $x_{i}$ 条件独立。这样做的好处是，当数据的分布的确接近于假设的那样，那么生成学习算法便会以较少的训练数据从而取得较好的效果。反观判别学习算法，由于其对于数据的包容性较强，鲁棒性较好，因此适用于的场合更多，需要更多的数据进行训练。二者的权衡，将为我们在实际解决问题中，提供一个启发。

生成学习算法_高斯判别分析_朴素贝叶斯_斯坦福CS229_学习笔记