EM算法_斯坦福CS229_学习笔记

Part VII EM算法（Expectation-Maximization Algorithm）

翻过学习理论的篇章，这一讲关注于非监督算法。首先由经典的K-means算法引出EM算法，最后利用混合高斯模型对于EM算法进行简单阐述。

Part VII EM算法（Expectation-Maximization Algorithm）

1 K-means算法

2 EM算法（Expectation-Maximization Algorithm）

2.1 Jensen不等式（Jensen's Inequality）

2.2 EM算法思想

2.3 EM算法在混合高斯模型（GMM）中应用

3 小结

1 K-means算法

非监督学习与之前监督学习的不同在于其输入的数据并没有数据标签。因此非监督学习的算法常常解决的是聚类问题，而其中比较经典且被熟知的便是K-means算法。现对K-means算法做一个介绍。K-means算法事先假设存在着k个聚类中心（这也是该算法的缺陷所在），通过迭代到收敛将每个样本归到相应的类别。

假设m个输入数据集合为 $\left \{ x^{(1)},..., x^{(m)}\right \}$ ，K-means算法步骤如下：

（1）在取值空间内，随机选取k个初始聚类中心，假设为 $\mu _{1},...,\mu _{k}$ 。

（2）重复以下两个步骤，直到收敛：

（i） $c^{(i)}$ 代表每个样本归属的类别，即对于每个样本 $x^{(i)}$ ，固定样本中心不变，计算

按照欧式距离，寻找该样本点距离最近的聚类中心，将样本重新进行归类。若样本点 $x^{(i)}$ 距离第n个中心最近，那么 $c^{(i)}=n$ 。（对应于EM算法中的E-step）

（ii）对于每个聚类中心 $\mu _{j}$ ，固定样本的类别不变，计算

调整新的样本中心的位置，即将属于该类的所有样本的均值作为新的聚类中心。（对应于EM算法中的M-step）

下图为K-means算法的流程。观察下图便很清晰了。其中（a）为原始数据分布，（b）为初始选择的两个聚类中心（k=2）。（c）-（f）为迭代收敛过程。

流程明白了，那么怎么保证上述流程收敛呢？

可以这么理解。我们先定义如下失真函数（distortion function，为什么这样叫，我也不清楚）

观察失真函数可发现，我们在迭代过程的两步实际就是对于该函数利用坐标下降法（还记得在SVM中里使用的坐标上升法吗？）求最小值的过程。迭代过程中的第一步便是固定 $\mu$ 不变，以x为参数进行求解使J最小；而第二步是固定 x 不变，以 $\mu$ 为参数求解使J最小。既然每一步都在使J最小，那么迭代过程显然是收敛的。

实际应用K-means时会发现，其结果容易受初始聚类中心的影响，因为注意到失真函数J（c， $\mu$ ）是一个非凸函数，也就是说会存在着一些局部最小值，使迭代很容易陷入局部最小值而不能得到全局最小值。常常通过选取多次不同的初始聚类中心进行多次试验来解决该问题。

2 EM算法（Expectation-Maximization Algorithm）

K-means算法与EM算法思想如出一辙，或者说是K-means算法是EM算法一种形式。K-means算法用来解决聚类问题，那么EM算法的提出是为了解决什么呢？个人理解，EM算法更像是一个工具性的算法，其目的在于提供了一种求解最大似然方程的思路。当遇到似然方程很难求解时，可利用EM算法的思路进行求解，EM算法的核心思想在于引入一个隐变量作为条件，在此条件下将似然方程的参数求解拆分为E-step与M-step，通过不断迭代直到收敛，从而得到相应的参数。

2.1 Jensen不等式（Jensen's Inequality）

EM算法的推导需要利用Jensen不等式。

首先回顾一下凸函数的定义。设 $f(x)$ 的取值域为实数。若 $\forall x\in R$ ，都有 $f^{''}(x)\geq 0$ （若x为向量，即相应的Hessian矩阵H半正定，即 $H\geq 0$ ），那么称 $f(x)$ 为凸函数。严格一点，若 $f^{''}(x)> 0$ （ $H> 0$ ），那么此时称 $f(x)$ 为严格凸函数。在此基础之上，引出Jensen不等式。

若 $f(x)$ 为凸函数，且有随机变量X，那么以下不等式称为Jensen不等式。

更进一步，不等式取等号的条件为： $f(x)$ 为严格凸函数；且 $p(X=EX)=1$ （即随机变量为常数）。

结合图来看看，就会明白该不等式了。假设 $f(x)$ 为凸函数，绘制以下图。

其中 $E[x]$ 为横轴中点。 $E[f(X)]$ 为纵轴中点。是不是就会觉得 $E[f(X)]\geq E[X]$ 就很直观了。

注意，在Jensen不等式中，若 $f(x)$ 为凹函数，那么原不等式方向相反，且不等式取等号条件相应更改。这在接下来推导EM算法中将会使用。

2.2 EM算法思想

EM算法为难以求解的似然方程提供了一个求解思路。以下为了推导方便，针对离散型随机变量而言，连续型随机变量将求和变为积分即可。

假设有输入数据集 $\left \{ x^{(1)},..., x^{(m)}\right \}$ ，原始方法对于x进行建模，参数为 $\theta$ ，得到 $p(x;\theta )$ ，由此写出似然方程

此时如果发现很难通过常规的求偏导的方式解此方程，为了解决此问题，EM算法提供了另一种求解思路。即假设在模型中还存在着一个潜在的随机变量z（我的理解是这相当于引入了一个条件进行限制），那么此时不再对于x建模，而对于（x，z）建模，则可将方程改写为

这种思想在接下来的因子分析中也会遇到。加入了一个潜在的随机变量其实有点像加入了一个限制条件，因为通常来说，一个方程给的条件越多，那么相对而言求解也会更轻松。并且还有一个好处在于，如果我们对于这个潜在的随机变量z“已知”的话（EM算法采用不断迭代的方式去逼近，从而达到了z已知的效果），那么求解该方程也会更为简单。

在此基础上，假设对于每个样本i， $Q_{i}$ 为z所服从的分布（ $\sum Q_{i}(z)=1,Q_{i}(z)\geq 0$ ），那么可将似然方程进行如下推导：

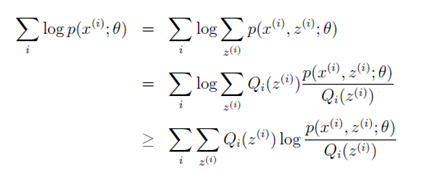
第一行为前文的结论。

第二行在第一行的基础之上，同时乘以一个 $Q_{i}(z^{(i)})$ ，除以一个 $Q_{i}(z^{(i)})$ 。经过这么变换后，可发现其实

$\sum _{z^{(i)}}Q_{_{i}}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta )}{Q_{i}(z^{(i)})} = E[\frac{p(x^{(i)},z^{(i)};\theta )}{Q_{i}(z^{(i)})}]$

回头再结合Jensen不等式，对比之下得

$X=\frac{p(x^{(i)},z^{(i)};\theta )}{Q_{i}(z^{(i)})}$ ，且 $f(x) = log(x)$

此时由于，因为 $f^{''}(x) =-\frac{1}{x^{2}}< 0$ ，即 $f(x) = log(x)$ 为严格凹函数，根据凹函数情况下的Jensen不等式 $f(EX)>E[f(X)]$ ，那么就可由第二行推出第三行（确保明白这里）。

明白我们的目的是使似然方程最大化，那么什么时候会最大呢？显然，两边取等号时，得到最大值。结合Jensen不等式的取等号条件： $f(x)$ 为严格凹函数，且X为常数时，不等式两端取等号。那么可设X为常数c，得下式：

那么 $Q_{i}(z^{(i)}) = \frac{p(x^{(i)},z^{(i)};\theta)}{c}$ ，结合定义 $\sum_{z} Q_{i}(z^{(i)})=1$ ，

得 $\sum_{z} Q_{i}(z^{(i)}) = \sum_{z} \frac{p(x^{(i)},z^{(i)};\theta)}{c}=1$ ，从而 $c= \sum_{_{z}} p(x^{(i)},z^{(i)};\theta)$ 。

将c带入原式可得 $\frac{p(x^{(i)},z^{(i)};\theta )}{Q_{i}(z^{(i)})}=c= \sum_{_{z}} p(x^{(i)},z^{(i)};\theta)$ ，即 $Q_{i}(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta )}{\sum_{_{z}} p(x^{(i)},z^{(i)};\theta)}$ 。由此可得下列推导。

原来固定参数 $\theta$ 不变的情况下，要使似然性最大，即 $l(\theta )$ 最大，隐变量z的分布选取后验分布即可。那么后验分布

由此，给出EM算法的迭代步骤：

（1）初始化参数 $\theta$ 。

（2）重复以下步骤直到收敛。

（i）E-step：对于每一个样本i，更新后验分布。

（ii） M-step：在z分布已知的情况下，最大似然法求解参数 $\theta$ 并进行更新。

E-step：固定当前参数 $\theta$ 不变，以后验分布 $p(z|x;\theta )$ 作为z的分布进行统计计算。这一步骤也被理解为给当前的似然函数 $l(\theta )$ 设置了一个下界。

M-step：由Jensen不等式推导而来，相当于z的分布已知，固定当前z分布不变，利用最大似然法计算得到参数 $\theta$ 。这相当于在上一步的 $l(\theta )$ 下界的基础上，利用最大似然法寻找该下界的最大值。

不明白没关系，又到了看图说话的时候了。结合下图进行分析。 $l(\theta )$ 如图中大圆弧所示。假设当前迭代的次数为t，输入参数为 $\theta^{t}$ 。那么E-step便是根据此时参数 $\theta^{t}$ ，得到一个隐变量z后验分布，如图中左下的蓝色圆弧所示，这便相当于确定了一个下界；M-step便是在此z后验分布基础上，通过最大似然法寻找参数 $\theta$ ，最大值即图中的红色小三角形处，此时的最大值即为 $\theta^{t+1}$ ，这便是使下界最大。之后进行判断，若收敛结束迭代；不收敛将 $\theta^{t+1}$ 传入下次迭代（t+1）。

要判断EM算法收敛的思路也很清晰，即判断在任意t和t+1时刻，是否都满足 $l(\theta^{t+1} )\geq l(\theta^{t} )$ 。仔细缕清迭代的过程，不难得到以下不等式（来源于博主Njiahe），确保你明白，不明白的话再去缕缕迭代过程：

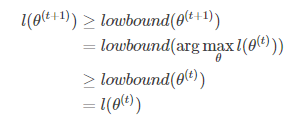
因此可以判断EM算法是收敛的。同样，也可以换个角度进行理解。可进行如下定义：

EM算法可看作是对于函数 $J(Q,\theta )$ 利用坐标上升求极值的过程。E-step固定参数 $\theta$ ，使Q最大；而M-step固定Q，使 $\theta$ 最大。如此进行迭代，计算过程当然是收敛的。

可能仍然会感到抽象，接下来利用EM算法，结合高斯混合模型进行推导，加深理解。

2.3 EM算法在混合高斯模型（GMM）中应用

混合高斯模型（Mixtures of Gaussians Model，GMM）是常用的建模模型。现在将EM算法应用其中。

同样假设有一组训练数据 $\left \{ x^{(1)},..., x^{(m)}\right \}$ ，假设存在着隐变量z，此时我们建模的目标为联合概率分布 $p(x,z)$ 。

联合概率分布可以写成 $p(x,z)=p(x|z)*p(z)$ 。由此我们进行GMM的建模。

对于每个样本i，有 $p(x^{(i)},z^{(i)})=p(x^{(i)}|z^{(i)})*p(z^{(i)})$ ，设z服从多项分布，且取值范围为1到k。

即 $z^{(i)}\sim Multinomial(\phi ) ,(\phi _{j}\geq 0,\sum_{j=1}^{k}=1,p(z=j)=\phi _{j})$

并且当给定z时，即 $z^{(i)}=j$ 时，有 $x^{(i)}|z^{(i)}\sim N(\mu _{j},\Sigma _{j})$ 。

即假设隐变量z的取值有k个，当每选定一个z=j（j=1,2，k）后，x便可确定为一个参数为 $\mu _{j},\Sigma _{j}$ 的高斯分布。这种模型我们称为高斯混合模型。注意此时的混合高斯模型与之前在生成学习算法中的高斯判别分析（GDA）建模的模型存在着两个不同：

（1）GDA中z服从于伯努利分布，而此时z服从于多项分布。这相当于一个扩展。

（2）GDA中两个高斯分布的协方差阵假设一样，而这里每个高斯分布的均值和协方差阵都不一样。

接下来应用EM算法进行参数求解。

在该模型中，参数为 $\phi ,\mu,\Sigma$ 。首先初始化各个参数的值。然后写出最大似然方程：

在E-step中，计算后验概率，即z属于每一类的概率。

将E-step中得到的结果带入M-step，进行最大似然方程求解，得到以下参数：

结果看上去也并不意外，在意料之中。这便是EM算法实际的应用了。

同理，可以回头再看一下K-means算法。其实迭代中的两个步骤就是EM算法的E-step与M-step。只不过在K-means中，潜在变量z服从的是狄拉克分布（Dirac Delta，即为高斯分布的极限），即每个样本只可能属于一种类别且属于其他类别的概率为0。因此K-means也被称为hard EM（是不是和softmax、hardmax近似）。

3 小结

EM算法作为一种求解最大似然方程的思路，在于增加了一个隐变量作为条件，通过迭代的方式使难以求解的最大似然方程得到求解。但是EM算法的一个缺陷在于，其较大程度上受初值的影响，而且会因此陷入局部最小值无法得到全局最小值。因此，在应用EM算法时，应多选取不同的初始条件进行初始化，综合考虑迭代的结果，从而得到最终的结论。