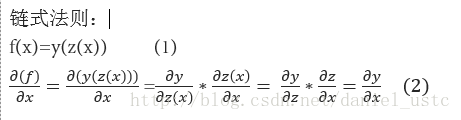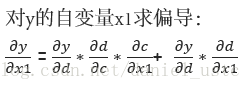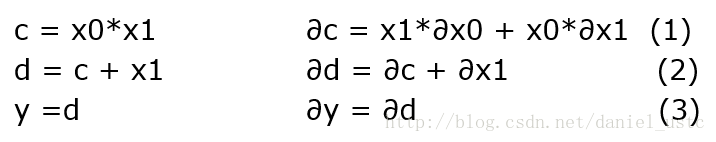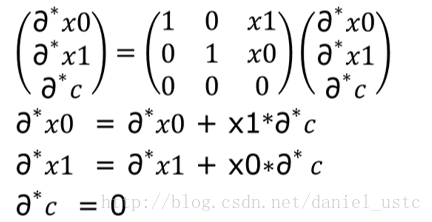C++自动微分（Automatic differentiation）原理1

0. 缘由

下面介绍下为什么要引入自动自动微分(automatic differentiation -> AD )。

一个优化问题的例子
假设现在我们在解决一个机器学习的问题，有了一些训练样本，现在需要寻找一个最优的函数，使得函数对输入X的估计Y’与实际输出Y之间的期望风险最小化。利用已知的经验数据（训练样本）来计算得到的误差，被称之为经验风险。使用对参数求经验风险来逐渐逼近理想的期望风险的最小值，就是我们常说的经验风险最小化（Empirical risk minimization，ERM）原则。我们利用经验风险最小化的原则求解机器学习的步骤为：
定义一个模型，这个模型有一定的参数，其能够在给定输入后根据模型预测输出；
定义一个损失函数(loss function)，这个损失函数能够计算出真实值和模型预测值的误差，比如平方损失、对数损失、0-1损失等等（损失函数尽量是一个凸函数，便于收敛计算）；
获得一些训练数据；
在训练数据上利用ERM原则对模型参数进行拟合，为防止过度拟合的模型出现（过于复杂的模型），在损失函数里增加一个每个特征的惩罚因子，即加入正则化项。

上面所述的在训练数据上结合ERM原则对模型参数进行拟合的过程其实就是一个机器学习的过程。机器学习的目标就是最小化我们的损失函数，当各个参数学到一定程度后，我们的损失函数也收敛，即达到最小值，这个学习的过程需要以下步骤：

写出在训练数据上关于模型参数的损失函数；
对损失函数求解关于不同模型参数的偏导；
写代码求解导数；
基于损失函数的参数学习算法现存的算法比较多:SGD,LBFGS,AdaGrad…；

上面求解方法存在的问题：

在相关函数的参数求导以及写出求导代码花费很多精力;
自己推导偏导及写代码求导，往往一步不慎，全盘皆输（这样做很容易出错）；
我们不必什么都要亲力亲为，应该把更多精力放在新的模型和实验上；

几种微分求解的方法

根据这篇paper：Automatic differentiation in machine learning: a survey中的介绍,目前微分求解有如下的方法：

手动求解法(Manual Differentiation)
数值微分法(Numerical Differentiation)
符号微分法(Symbolic Differentiation)
自动微分法(Automatic Differentiation)

下面说下各自的优缺点：
1. 手动求导效率低下、易于出错。
2. 数值微分：根据导数定义有：
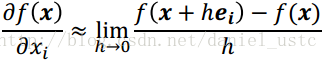
num diff1
数值微分易于实现，但参数多时计算量较大，且引起的round off error(舍入错误)和truncation error(截断错误), 使用center difference(中心差分)可以减少truncation error但是，存在rouding error, 往往我们利用Numerical Differentiation来检验其它微分算法的正确性，如在BP计算的时候，gradient check就是利用数值微分法进行check point。
center difference：

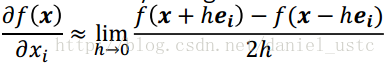
3.符号微分是为了解决手动微分以及数值微分的缺点而提出来的，其利用代数软件，实现微分的一些公式，它试图将问题转化为一个纯数学符号问题。符号微分的缺点是它经常导致复杂、晦涩难懂的表达式，最终出现“表达式膨胀”（expression swell）问题，它使得问题符号微分求解的表达式急速“膨胀”，导致最终求解速度变慢。
4.自动微分利用链式法则达到自动求导的效果。

自动微分法是一种介于符号微分和数值微分的方法：数值微分强调一开始直接代入数值近似求解；符号微分强调直接对代数进行求解，最后才代入问题数值；自动微分将符号微分法应用于最基本的算子，比如常数，幂函数，指数函数，对数函数，三角函数等，然后代入数值，保留中间结果，最后再应用于整个函数。因此它应用相当灵活，可以做到完全向用户隐藏微分求解过程，由于它只对基本函数或常数运用符号微分法则，所以它可以灵活结合编程语言的循环结构，条件结构等，使用自动微分和不使用自动微分对代码总体改动非常小，并且由于它的计算实际是一种图计算，可以对其做很多优化，这也是为什么该方法在现代深度学习系统中得以广泛应用。

1. Automatic differentiation (AD)

在数学和计算代数领域，automatic differentiation (AD)又称为 algorithmic differentiation 或者 computational differentiation。AD是一个可以对程序代码表示的数学函数进行自动微分的技术。AD利用链式法则来达到自动求解的目录，AD有两种主要的方法：

代码转换（source-code transformation）（R. Giering and T. Kaminski. 1998）：
- 利用一个代码转换编译器，这个编译器会分析源代码，然后产生一个和源代码对应的伴随模式(adjoint model)程序，编译时的代码生成（如用 flex-bison 做词法、语法分析）；
- 优点是静态生成效率高(原始算法的3~4倍) ;
- 一次生成，多次使用，缺点是学习门槛较高（编译原理…）；
- 很多比较好的工具非免费；
- 对现代编程语言特性的限制（如C++类、模板等）；
运算符重载(operator overloading)
- 应用比较广泛，很多编程语言特性可以很好的工作；
- 优点是简单直接，缺点是动态生成成本较高（代表性的工具效率是原始算法的10~35倍）。
- 较多免费开源 C++ 工具 (e.g. ADOL-C, CppAD, Sacado)；

AD 这两种实现方式：运算符重载与代码生成，两种方式的原理都一样，链式法则。AD相关工具，请到这个http://www.autodiff.org/页面。自动微分（AD）是计算导数的最优方法，比符号计算、有限微分更快更精确，AD已经广泛应用在优化领域，包括人工神经网络的训练算法 back-propagation（BP）等。

2. AD基本原理

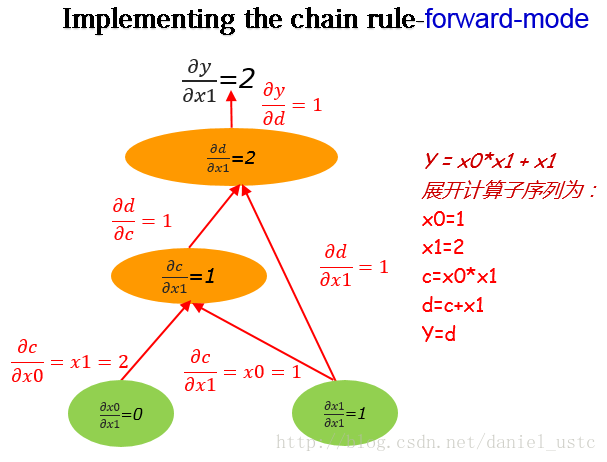
不难想象，任何计算都可以由第1步到第k步的序列形式，其中第 i 步计算的输入，在之前的 i-1 步中已经计算（例如编译器生成的汇编指令序列）。因此，任何计算都可以看作形式如子计算序列的复合函数，结合微积分中的链式法则AD有forward-mode 和reverse mode两种计算方式。下面结合实际的例子进行说明：

计算图

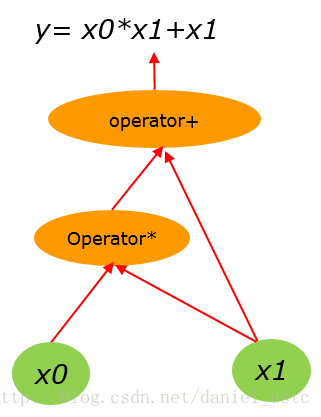
假设有算术计算公式：

y= x0*x1 + x1 （1）

(1)式用计算图表示为：

cg1

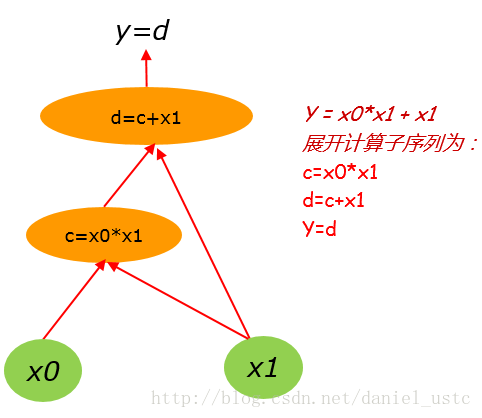
把(1)式展开计算子序列为：


c=x0*x1     
d=c+x1      
y=d

对应的计算图为：

cg2

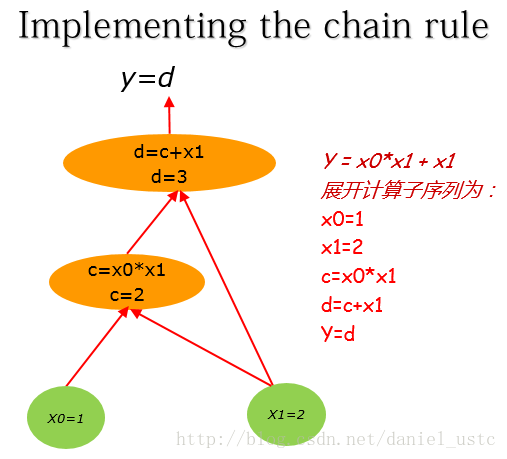
这里假设x0,x1的初值分别为：1, 2。把(1)式展开计算子序列为：

x0=1        
x1=2          
c=x0*x1     
d=c+x1      
y=d

对应计算图为：
这里写图片描述

计算图上的导数求解
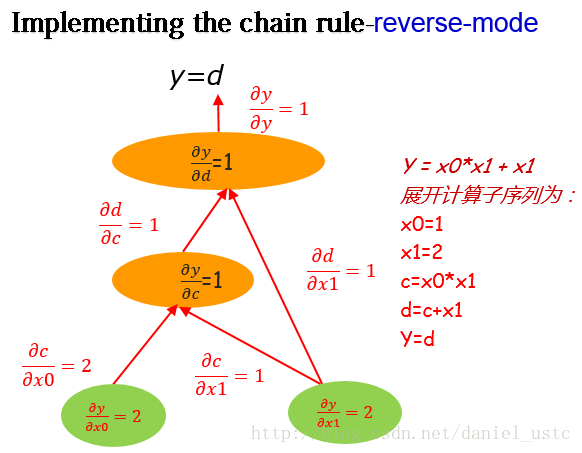
理解计算图上的导数求解的关键是要理解：边上的导数。x0直接影响到c,如果x0改变，那么c会发生什么变化？对于这种情形我们称它为c关x0的偏导数。

为了计算计算图上的偏导数，我们需知道导数的加法和乘法原则：

der rule
利用上面两个原则结合计算图，其中图中的边即为偏导数则有：

cg rule

有了上面的计算图，为了求偏导dy/dx0, 我们还需知道链式法则, 简单概括起来即为：“由两个函数凑起来的复合函数，其导数等于里边函数代入外边函数的导数（注意，里面的函数看成一个自变量了），乘以里边函数的导数”，数学表达式即为：

chain rule

因此结合导数的加法和乘法原则以及链式法则，可知对于特点节点的偏导数及法则是：
一个节点对另一个节点求偏导，对从这个节点到另个所有路径进行累加，其中每条路径上的值是这条路径所有边进行累积。举个例子比如y对x1求偏导：

part

利用上述公式结合x0=1，x1=2的初始值可知，dy/dx1= 1*1*1+1*1 = 2 ,符合实际结果。

forward-mode 和 reverse-mode

微分流形上的矢量有两种：切空间 (Tangent space)的矢量和对偶空间 (Dual space)的矢量。
其中切空间的基 $\{\frac{\partial}{\partial x_i}\}$ 是关于坐标系的偏导,对偶空间的基是关于坐标系的微分 $\{d x^i\}$ 。从切矢量出发可以得到自动微分的正序模式 (forward mode, tangent-linear)，从对偶矢量出发可以得到自动微分的逆序模式 (reverse mode，adjoint mode,backward mode)。

1. forward-mode
任意切矢量 $\dfrac{d}{ds}=\dfrac{dx^{i}}{ds}\dfrac{% \partial }{\partial x^{i}}$ 的定义是其对应的方向导数算符将它依次应用在计算序列的左侧便可获得下图左侧的张量公式:

tangent
对张量（Tensor）变换即可得上图右侧的矩阵公式。其中， $J$ 便是一阶导 Jacobian 矩阵,这种计算导数的方式与展开的计算子序列顺序相同，所以正序模式每一个方向导数的计算复杂度与计算序列相同空间复杂度也相同。

对于算式(1)：

$y= x0*x1 + x1$ （1）

如求 $y$ 对 $x_1$ 的偏导其对应的forward-mode计算序列为：

$\dfrac{\partial x_0}{dx_1}=0$

$\dfrac{\partial c}{dx_1}=x_0$

$\dfrac{\partial d}{dc}=1$

$\dfrac{\partial d}{dx_1}=1$

$\dfrac{\partial d}{dx_1}=\dfrac{\partial d}{dc}\dfrac{\partial c}{dx_1}+\dfrac{\partial x_1 }{\partial x_1}$ (sum rule)

在计算图上自底向上求关于 $x_1$ 的偏导，如下图：

forward model x1

从图中我们可以看出来，利用forward-mode对 $x_1$ 求偏导，可以得到所有节点关于 $x_1$ 的偏导。即forward-mode可以求出所有输出关于某一个输入的偏导数，注意这里一次forward计算只得到所有输出关于某一个自变量的偏导数，如果输入（自变量）是n维的，想得到输出关于其它输入（自变量）的偏导数，则需要计算多次。
注意若计算序列的自变量有 n 维，则获得 Jacobian 矩阵需要计算 n 个方向上的方向导数。
2. reverse-mode
任意对偶矢量 $d_{t}=t_{i}dz^{i}$ 的定义是其对应方向的微分
对该矢量做关于坐标基 $\left\{ dx^i \right\}$ 的坐标变换便可获得下图左侧的张量公式:
dual

对张量缩并可得上图右侧的矩阵公式，其中 $D += TP$ 表示叠加 $D = D + TP$ ， $D_x$ 便是关于x的一阶导。这种计算导数的方式与计算序列逆序，所以称为逆序模式(reverse-model)。问题来了，如何得到这种逆序方式呢？
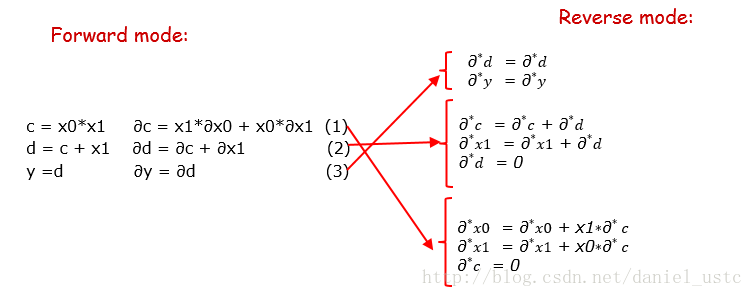
关于如何求这种逆序模式，前人已经有所研究，Recipes for adjoint code construction, 结合论文的思路举个例子说明吧，对于计算式：
$y= x0*x1 + x1$

上面展开对应的子序列及其微分如下图：

adjoint

对于上面图左侧，逆序模式是对图中右侧计算子序列的微分形式的逆序求解伴随模式序列，然后按照伴随模式的顺序计算即可得到相关变量的偏导数，关于伴随模式的求解方法，其实比较简单，知道矩阵的转置是怎么回事就能求出adjoint code，关于上图式(2)微分表达式及其矩阵形式如下图：

adjoint code 2

对上图等式右侧的矩阵进行转置即可得到式(2)对应的伴随模式所对应的计算序列，如下图所示：

adjoint_3

图中转置矩阵展开后的三个表达式即为公式（2）对应的伴随模式代码（也即逆序模式对应的代码），把计算子序列的微分形式按照这种方式逆序展开即为逆序模式的计算序列，把前序模式对应的微分表达式逆序展开为伴随表达式，即为下图所示：

adjoint_4

这里注意d其实就是y的别名因此表达的意思所以一样的，下面我们根据adjoint 计算序列来写出reverse-mode求解偏导的代码：

#include <cmath>
#include <iostream>
using namespace std;

double reverse_AD(const double x[2], double y_ad[1], double x_ad[2]) {
    double c = x[0] * x[1];
    double d = c + x[1];
    double y = d;

    /* Adjoint part: */
    // init
    double d_ad = 0, c_ad = 0;

    d_ad = y_ad[0]; // 1

    c_ad = c_ad + d_ad;   // 2
    x_ad[1] = x_ad[1] + d_ad;
    d_ad = 0;

    x_ad[0] = x_ad[0] + x[1] * c_ad; // 3
    x_ad[1] = x_ad[1] + x[0]*c_ad;
    c_ad = c_ad;

    return y;
}

int main()
{
    double x[] = { 1.0, 2.0 };
    double y_ad[1] = { 1.0 };// init to 1
    double x_ad[2] = { 0, 0 };
    double y = reverse_AD(x, y_ad, x_ad);
    cout << "y=" << y << "\n";
    cout << "dy/dy=" << y_ad[0] << "\n";
    cout << "dy/dx0=" << x_ad[0] << "\n";
    cout << "dy/dx1=" << x_ad[1] << "\n";
    return 0;
}

输出为：

y=4
dy/dy=1
dy/dx0=2
dy/dx1=2

利用reverse-mode在计算图上从图顶部y向下求解偏导，我们可以得到输出关于所有节点的偏导数，如下图：

reverse cg

从图中以及上面的程序也能看出来，reverse-mode从上至下计算，我们能够获得输出关于所有节点的偏导（当然包括所有自变量，即这里的x0,x1）。对比上面介绍的forward-mode，利用 forward-mode一次计算，我们只能得到关于某一个自变量的偏导数。因此，试想我们在机器学习中有这样一个优化函数，它有上百万个参数，如果利用 forward-mode求解这些参数的偏导，那么需要计算百万次，这是一个很耗费时间的事情，但是如果利用reverse-mode仅仅需要计算一次，我们就能得到关于所有参数的偏导数。所以基于reverse-mode的这一特性，现在流行的深度学习框架中，神级网络模型训练的BP算法基本也是利用reverse-mode进行求解的。

虽然reverse-mode有诸多优点，但是forward-mode也有它自身的优点（比如方法简单易懂，不需要保存很多中间变量，reverse-mode就需要保存挺多中间变量的…）。因此何时用正序模式何时用逆序模式？
取决于自变量维度 n 与因变量维度 m，若 n > m 则逆序更快若 n < m 则正序更快。

如何实现reverse-mode？有兴趣的读一下这篇论文：
“Fast Reverse-Mode Automatic Differentiation using Expression”

参考

R. Giering and T. Kaminski. 1998. Recipes for adjoint code construction. ACM Trans. Math. Softw. 24, 437–474. down
https://en.wikipedia.org/wiki/Automatic_differentiation
Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition
The Art of Differentiating Computer Programs: An Introduction to Algorithmic Differentiation
http://colah.github.io/posts/2015-08-Backprop/
https://www.zhihu.com/question/48356514/answer/123290631
Automatic differentiation in machine learning: a survey