自动微分（Auto differentiation）机制详解

自动微分是一种能够用计算机程序计算函数导数数值的一种方法，其基本原理是导数运算法则。由于它能够在无需手动推导公式的情况下求函数函数各个自变量的一阶导数，所以自动微分的基本思想与方法在深度学习框架中广泛应用。在自动微分法出现之前，也有数值微分、符号微分等方法，这些方法虽然也很巧妙，但难以广泛应用于实际问题中。

一：基本原理

1.正向传播

自动微分的原理是求导法则，算法结构类似于递归树。对于一个多元函数式f(x1,x2..,xn)，它的运算总可以看成是两个自变量或自变量与常数的加法与乘法运算，如:

$f(a,b,c,d)=2\times a \times b+c \times c\times d+d\times d$

它的运算树图可以表示为：

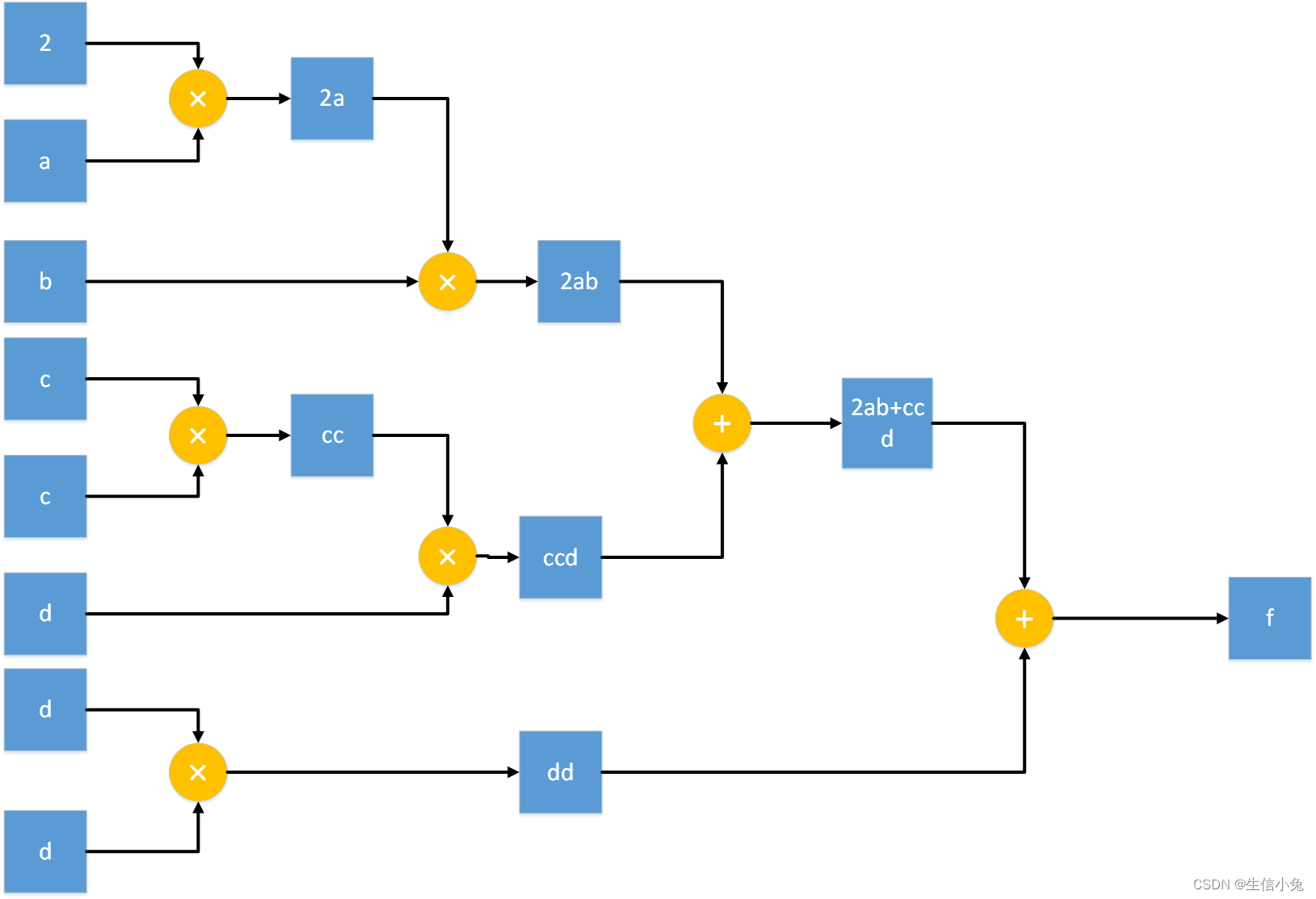
我们发现，任何的运算都可以逐步拆解成两个元素的运算，并且只有加法和乘法两种，如果是多个加法和乘法，也是两个叶节点逐步回归到根节点的这个过程。这个从叶节点逐步回到根节点这个过程即为正向传递，这是求函数对其中任一自变量求偏导数(梯度)的第一步。对于张量而言，运算会更加丰富，但整个树的结构是一致的。

class auto:
    def __init__(self,value):
        self.value=value
    def __add__(self,other):
        return auto(value=self.value+other.value)
    def __mul__(self, other):
        return auto(value=self.value*other.value)
    def multiply(self,other):
        return auto(value=np.multiply(self.value,other.value))
    def dot(self,other):
        return auto(value=np.dot(self.value,other.value))
if __name__=='__main__':
    a=auto(1)
    b=auto(2)
    c=auto(3)
    f1=a*b+c
    d=auto(np.random.randint(0,2,size=(3,2)))
    e=auto(np.random.randint(0,2,size=(2,3)))
    f2=d.dot(e)
    print('f1',f1.value)
    print('f2',f2.value)

在运算之前，我们把数或矩阵转成auto对象，之后就可以用auto中的函数来进行相应的运算。这里的__add__与__mul__是重写了一遍数的加法和乘法内置方法，这样就可以用‘+’，‘*’来直接运算。当然也可以直接定义add函数，mul函数，这样a+b就需要改成a.add(b)，最终的效果是一样的。（其实仔细想一下，这样的方法在很多方面都有所体现，如numpy、pytorch等库，它们进行运算时是需要将数据转成相应的array或tensor对象，然后才能运算，并且运算的方式也与这个方式类似。）

这里之所以用auto对象，是因为它可以在运算的过程中逐步递归，可以在正向传递过程中保存产生某一节点的两个子节点与这两个节点的运算方式，从而才能进行后面的反向传播求导。

2.反向传播

之所以是方向传播，是因为我们正向传播构造好这棵运算树后，求导的过程是从根节点逐步向叶节点传递的。仍以1中f(a,b,c,d)为例，我们首先计算f对f自己的偏导，结果为1(这一步理论上可以省去，但是在矩阵运算中是不能省去的)；f对（2ab+ccd）的偏导是1；f对dd的偏导是1；之后f对2ab的偏导为：

$\frac{f}{f}.\frac{\partial f}{\partial 2ab+ccd}.\frac{2ab+ccd}{2ab}=1\times 1\times1=1$

此时我们发现，要想求函数对某一变量的导数，就需要知道函数对这个变量的父节点的偏导，函数对某一节点的偏导值为函数对这个节点的父节点的偏导与父节点对该节点偏导的乘积。这样我们可以求f对a的偏导为：

$\frac{\partial f}{\partial a}=\frac{f}{f}.\frac{\partial f}{\partial (2ab+ccd)}.\frac{\partial (2ab+ccd)}{2ab}.\frac{\partial 2ab}{2a}.\frac{2a}{a} \\ =1\times1\times1\times b\times 2=2b$

最终的结果符合事实。

当然，在这里a只出现在一个分支中，若a在不同的分支上，结果会是多个链式乘法的求和。例如f=2a+2ab，它对a的导数为1×2+1×2×b=2+2b，在后面算法实现时需要注意这一点。

对于矩阵求导的情况，不能像数一样随意的由左向右依次相乘，因为矩阵求导是区分左乘与右乘的，并且有时也有矩阵的转置，这一部分可以参考兔兔之前的博客《矩阵求导（本质、原理与推导）详解》以及《多层感知机、全连接神经网络......详解》。兔兔在这里给出一个常用的矩阵求导结论：

$Y_1=W_1.A_1 \\Y_2=W_2.Y_1 \\ \Rightarrow \\ \frac{\partial Y_2}{\partial Y_1}=W_{2}^T .\frac{\partial Y_2}{\partial Y_2} \\\frac{\partial Y_2}{\partial W_2} =\frac{\partial Y_2}{\partial Y_2}.Y_{1}^T \\ \frac{\partial Y_2}{A_1}=W_{1}^T.W_{2}^T.\frac{\partial Y_2}{\partial Y_2} \\ \frac{\partial Y_2}{\partial W_1}=W_{2}^T.\frac{\partial Y_2}{\partial Y_2}.A_{1}^T$

这个规律还是比较容易发现的，对于矩阵乘法，如果被导的自变量在式子乘法坐标，则把另一个自变量转置右乘，反之左乘。如果把矩阵看成数，由于数的转置还是本身，并且符合乘法交换律，则退化到普通的函数求导了。把这个规律的算法写入auto对象里，就可以实现BP算法中求各个参数梯度，并且无需手动推导公式并进行复杂的算法实现。当然，对于卷积层，我们也可以写出(损失函数)对卷积核的偏导，本质上仍是矩阵求导。对于激活函数，我们仍然可以求导，只不过卷积运算一般只接收一个元素(除softmax等函数)，然后输出一个结果，规律方法是一致的。

二：算法实现

自动微分的难点在于算法实现，因为它是一种递归树结构，所以有时会比较难理解，类似的算法如决策树、蒙特卡洛树等也是如此。

对于自动微分，我们定义一个auto对象，它用于储存正向传递生成的运算树中某一节点的值(value)、子节点auto(depend)、子节点运算方式（opt），并且初始梯度(grad)为None或0。之后反向传播过程，会根据链式求导原理逐步求出函数对每个节点的导数。

import numpy as np

class auto:
    '''自动微分'''
    def __init__(self,value,depend=None,opt=''):
        self.value=value #该节点的值
        self.depend=depend #生成该节点的两个子节点
        self.opt=opt #两个子节点的运算方式
        self.grad=None #函数对该节点的梯度
    def add(self,other):
        '''数或矩阵加法'''
        return auto(value=self.value+other.value,depend=[self,other],opt='+')
    def mul(self, other):
        '''数的乘法或数与矩阵乘法'''
        return auto(value=self.value*other.value,depend=[self,other],opt='*')
    def dot(self,other):
        '''矩阵乘法'''
        return auto(value=np.dot(self.value,other.value),depend=[self,other],opt='dot')
    def sigmoid(self):
        '''sigmoid激活函数'''
        return auto(value=1/(1+np.exp(-self.value)),depend=[self],opt='sigmoid')
    def backward(self,backward_grad=None):
        '''反向求导'''
        if backward_grad is None:
            if type(self.value)==int or float:
                self.grad=1
            else:
                a,b=self.value.shape
                self.grad=np.ones((a,b))
        else:
            if self.grad is None:
                self.grad=backward_grad
            else:
                self.grad+=backward_grad
        if self.opt=='+':
            self.depend[0].backward(self.grad)
            self.depend[1].backward(self.grad) #对于加法，把函数对自己的梯度传给自己对子节点的梯度
        if self.opt=='*':
            new=self.depend[1].value*self.grad
            self.depend[0].backward(new)
            new=self.depend[0].value*self.grad
            self.depend[1].backward(new)
        if self.opt=='dot':
            new=np.dot(self.grad,self.depend[1].value.T)
            self.depend[0].backward(new)
            new=np.dot(self.depend[0].value.T,self.grad)
            self.depend[1].backward(new)
        if self.opt=='sigmoid':
            new=self.grad*(1/(1+np.exp(-self.depend[0].value)))*(1-1/(1+np.exp(-self.depend[0].value)))
            self.depend[0].backward(new)

if __name__=='__main__':
    a=auto(3)
    b=auto(4)
    c=auto(5)
    f1=a.mul(b).add(c).sigmoid()
    f1.backward()
    print(a.grad,b.grad,c.grad) #f1对a,b,c,导数
    A=auto(np.random.randint(1,20,size=(3,4)))
    B=auto(np.random.randint(1,20,size=(4,3)))
    F=A.dot(B)
    F.backward()
    print(A.grad,B.grad)

构造auto后，使用时把数或矩阵转成auto对象，用其中含有的运算函数进行运算，之后对最终的结果使用backward，就可以求出这个函数对各个自变量的梯度了。当然，对谁使用backward，就是谁对各个自变量求偏导。深度学习中通常是损失函数对参数求偏导。关于上述代码，感兴趣的学习也可以加上更多的函数，来丰富auto的功能。

细心的同学可以发现，在pytorch、tensorflow等深度学习框架中，也是用backward()这样的方法求梯度，和这里的用法几乎是一致的，这也说明这些深度学习框架的背后也是使用了自动微分这种方法，只不过更加复杂一些。

三：总结

自动微分法作为求梯度的方法，极大地促进了深度学习的发展，它使得我们摆脱手动推导公式并进行算法实现的繁琐操作，能够很方便地实现卷积、全连接、循环神经网络中梯度求解。虽然在实际应用中我们并不需要写自动微分算法，但是它的递归算法思想却是十分重要的，它能使我们更好地理解这一类算法的基本思想。