神经网络解决Logistic回归问题及公式向量化推导

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/quiet_girl/article/details/80033951

一、Logistic问题描述

1、训练集和测试集表示

(1) 有m个训练样本，训练集表示为：$\{(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}), ..., (x^{(m)},y^{(m)})\}$。其向量化表示为：

$$\begin{equation*} X = \begin{bmatrix} \cdot & \cdot & & & &\cdot \\ \cdot & \cdot & & & & \cdot\\ x^{(1)} & x^{(2)} & \cdot & \cdot &\cdot & x^{(m)}\\ \cdot & \cdot & & & &\cdot \\ \cdot & \cdot & & & & \cdot \end{bmatrix} \end{equation*}$$ $X$的维度是 $(n_x, m)$，其中 $n_x$表示一个样本的所有特征（举例：对于一个图片来说，其所有特征就是RGB下的所有的像素点，若图片大小为64*64，则 $n_x= 64 * 64 * 3$）。 $x^{(i)}$是一个向量，表示一个样本。
(2) m个样本对应m个label，因此Y的表示如下：
$$\begin{equation*} Y = \begin{bmatrix} y^{(1)} & y^{(2)} & \cdot & \cdot & \cdot & y^{(m)} \end{bmatrix} \end{equation*}$$ $Y$的维度是(1, m)。

2、Logistic回归

Logistic回归的方程是$y^{(i)}=\sigma(w^Tx+b)$，其中$\sigma(z^{(i)})=\frac{1}{1 + e ^{-z^{(i)}}}$。
给定训练集$\{(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}), ..., (x^{(m)},y^{(m)})\}$，我们希望样本的预测结果$\hat{y}^{(i)}$与实际结果$y^{(i)}$尽可能地接近。
其代价函数如下：
在Logistic回归模型中，我们并不使用平方和作为我们的目标函数，我们设定的目标函数如下：

$$\begin{equation*} L(\hat{y}, y) = - (y log\hat{y} + (1-y)log(1-\hat{y})) \end{equation*}$$ 为了验证其可行性，我们可将其分开考虑：
①若y=1，则 $L(\hat{y}, y) = - log\hat{y}$，若想要使得损失函数最小，则需要 $\hat{y}$最大，这满足回归的任务要求。
②若y=0，则 $L(\hat{y}, y) = -log(1-\hat{y})$，若想要使得损失函数最小，则需要 $\hat{y}$最小，也满足回归的任务要求。
因此，Logistic回归的代价函数便是所有样本的损失函数之和，使用公式表示如下：
$$\begin{align*} J(w,b) &= \frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) \\ &=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log{\hat{y}^{(i)}}+(1-y^{(i)})log{(1-\hat{y}^{(i)})}] \end{align*}$$ 下面的内容中为了方便运算，我们以L函数来进行分析，在最后的过程中才将其转化为J, $J = \frac{1}{m}L$

3、转化为神经网络预测模型

Logistic回归问题可以简单地转化为两层的神经网络(也可以叫做单隐层神经网络)，其结构图如下：

输入值 $x^{(i)}$是一个样本向量， $w$是参数，此预测模型先基于线性模型，然后经过激励函数得到最终的预测值。

二、前向传播和后向传播

1、前向传播

下面使用一简单的例子介绍前向传播，如下图：

前向传播和我们平时的思维是一致的，即给出输入，通过一次次变换得到输出。

2、后向传播

参数的更新过程是算法结果不断优化的过程：输入数据，根据前向传播可以得到预测值，将预测值和真实值进行比较，得到损失函数，基于损失函数，更新参数，使得每一次的迭代过程损失函数都会减小，这就是更新的主要思想。
下面主要讲后向传播及其推理过程，两层神经网络的模型如下：

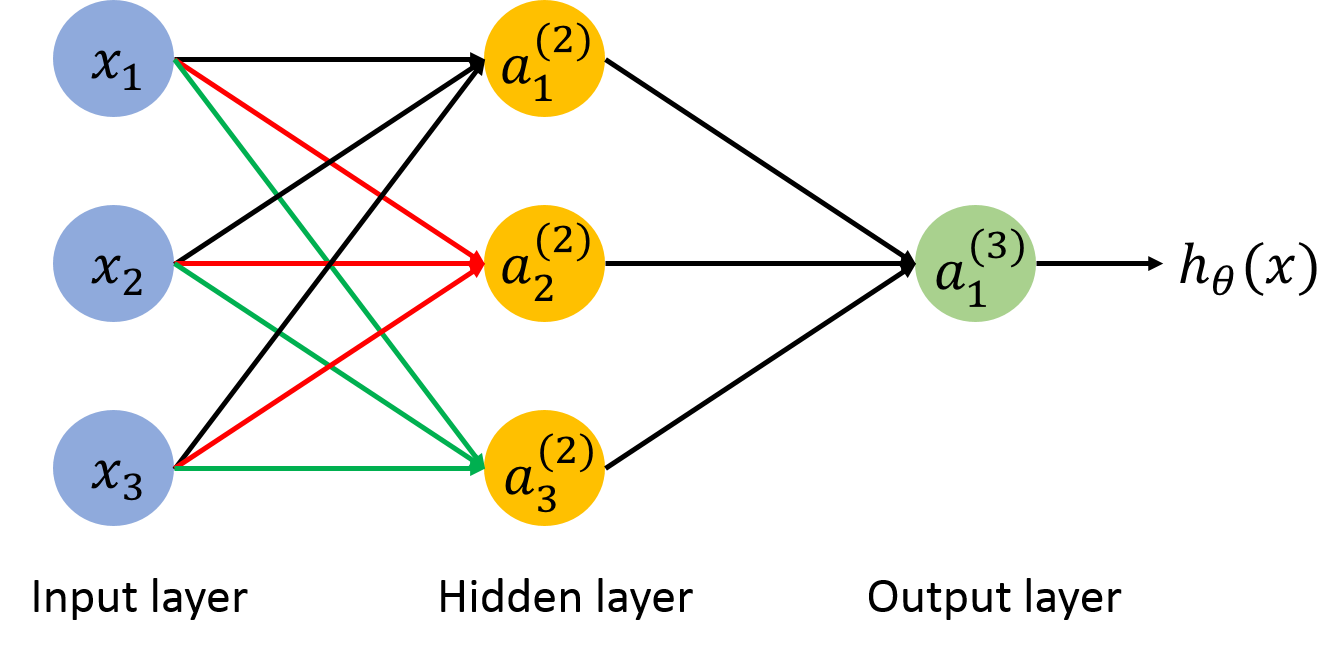
反向传播的过程就是从后向前更新参数的过程，更新参数的规则如下：
$$\begin{align*} w := w - \alpha \cdot \frac{dJ(w,b)}{dw} \\ b := b - \alpha \cdot \frac{dJ(w,b)}{db} \end{align*}$$
为了求取参数更新的公式，我们有如下的求导过程：
已知：
$$\begin{align*} z &= w^Tx + b \\ \hat{y} &= a = \sigma(z) \\ L(a,y) &= -(yloga+(1-y)log(1-a)) \end{align*}$$
求dw的过程：
$$\begin{align*} dw = \frac{L(w,b)}{dw} &= \frac{dL(w,b)}{da} \cdot \frac{da}{dz} \cdot \frac{dz}{dw} (链式法则) \\ & = (-\frac{y}{a}+\frac{1-y}{1-a}) \cdot a(1-a) \cdot x \\ &=(a-y)x \end{align*}$$ 又因为：
$$\begin{align*} dz = \frac{L(w,b)}{dz} &= \frac{dL(w,b)}{da} \cdot \frac{da}{dz} \\ &= (-\frac{y}{a}+\frac{1-y}{1-a}) \cdot a(1-a) \\ &= a-y \end{align*}$$ 因此： $dw = dz \cdot x$
求db的过程：
$$\begin{align*} db = \frac{L(w,b)}{db} &= \frac{dL(w,b)}{da} \cdot \frac{da}{dz} \cdot \frac{dz}{db} (链式法则) \\ & = (-\frac{y}{a}+\frac{1-y}{1-a}) \cdot a(1-a) \cdot 1 \\ &=a-y \end{align*}$$ 因此， $db=dz$

三、m个样本的梯度下降

下图是一次迭代过程的伪代码：

对于一次迭代的过程，便是先前向传播，更加前向传播的结果后向传播不断更新参数。
对于T次迭代过程的计算，只需要在一次迭代过程外面加一个for循环即可。

四、向量化

1、Z的向量化

$$\begin{align*} Z&=\begin{bmatrix} z^{(1)} & z^{(2)} & \cdot & \cdot & \cdot & z^{(m)} \end{bmatrix} \\ &=\begin{bmatrix} w^Tx^{(1)}+b & w^Tx^{(2)} +b & \cdot & \cdot & \cdot & w^Tx^{(m)}+b \end{bmatrix} \\ &= \begin{bmatrix} w^Tx^{(1)} & w^Tx^{(2)} & \cdot & \cdot & \cdot & w^Tx^{(m)} \end{bmatrix} + \begin{bmatrix} b & b & \cdot & \cdot & \cdot & b \end{bmatrix} \\ &=w^TX+b \end{align*}$$

2、A的向量化

$$\begin{align*} A &=\begin{bmatrix} a^{(1)} & a^{(2)} & \cdot & \cdot & \cdot & a^{(m)} \end{bmatrix} \\ &=\begin{bmatrix} \sigma(z^{(1)}) & \sigma{(a^{(2)})} & \cdot & \cdot & \cdot & \sigma{(a^{(m)})} \end{bmatrix} \\ & =\sigma(Z) \end{align*}$$

3、J的向量化

$$\begin{align*} J &= - \frac{1}{m} \sum_{i=1}^{m}[y^{(i)}loga^{(i)}+(1-y^{(i)})log(1-a^{(i)})] \\ &= - \frac{1}{m} \sum_{i=1}^{m}y^{(i)}loga^{(i)} - \frac{1}{m} \sum_{i=1}^{m}(1-y^{(i)})log(1-a^{(i)}) \\ &= - \frac{1}{m} (y^{(1)}loga^{(1)}+y^{(2)}loga^{(2)}+...+y^{(m)}loga^{(m)}) \\ & \qquad - \frac{1}{m} [(1-y^{(1)})log(1-a^{(1)})+(1-y^{(2)})log(1-a^{(2)})+...\\ & \qquad +(1-y^{(m)})log(1-a^{(m)})] \\ &= -\frac{1}{m} \begin{bmatrix} y^{(1)} & y^{(2)}& \cdot & \cdot & \cdot &y^{(m)} \end{bmatrix}\begin{bmatrix} loga^{(1)}\\ loga^{(2)}\\ \cdot \\ \cdot \\ \cdot \\ loga^{(m)} \end{bmatrix} \\ & \qquad - \frac{1}{m} \begin{bmatrix} 1-y^{(1)} & 1-y^{(2)}& \cdot & \cdot & \cdot & 1-y^{(m)} \end{bmatrix}\begin{bmatrix} log(1-a^{(1)})\\ log(1-a^{(2)})\\ \cdot \\ \cdot \\ \cdot \\ log(1-a^{(m)}) \end{bmatrix} \\ &= -\frac{1}{m}YlogA^T-\frac{1}{m}(1-Y)log(1-A^T) \end{align*}$$

4、dz的向量化

已知：

$$\begin{align*} dz^{(1)}&=a^{(1)}-y^{(1)} \\ dz^{(2)}&=a^{(2)}-y^{(2)} \\ ...\\ dz^{(m)}&=a^{(m)}-y^{(m)} \end{align*}$$
又因为：
$$\begin{align*} dZ &= \begin{bmatrix}dz^{(1)} &dz^{(2)}&\cdot&\cdot&\cdot&dz^{(m)} \end{bmatrix} \\ A & = \begin{bmatrix}a^{(1)} &a^{(2)}&\cdot&\cdot&\cdot&a^{(m)} \end{bmatrix} \\ Y & = \begin{bmatrix}y^{(1)} &y^{(2)}&\cdot&\cdot&\cdot&y^{(m)} \end{bmatrix} \end{align*}$$
因此：
$$\begin{align*} dZ&= \begin{bmatrix}dz^{(1)} &dz^{(2)}&\cdot&\cdot&\cdot&dz^{(m)} \end{bmatrix} \\ &=\begin{bmatrix}a^{(1)}-y^{(1)} &a^{(1)}-y^{(2)}&\cdot&\cdot&\cdot&a^{(m)} -y^{(m)}\end{bmatrix} \\ &= \begin{bmatrix}a^{(1)} &a^{(2)}&\cdot&\cdot&\cdot&a^{(m)} \end{bmatrix} - \begin{bmatrix}y^{(1)} &y^{(2)}&\cdot&\cdot&\cdot&y^{(m)} \end{bmatrix} \\ &=A-Y \end{align*}$$

5、dw的向量化

$$\begin{align*} dw &= \frac{1}{m}(x^{(1)}dz^{(1)}+x^{(2)}dz^{(2)}+...+x^{(m)}dz^{(m)}) \\ &=\frac{1}{m} \begin{bmatrix} x^{(1)} & x^{(2)} & \cdot & \cdot & \cdot & x^{(m)} \end{bmatrix} \begin{bmatrix} dz^{(1)}\\ dz^{(2)}\\ \cdot\\ \cdot\\ \cdot \\ dz^{(m)} \end{bmatrix} \\ &= \frac{1}{m}XdZ^T \end{align*}$$

6、db的向量化

$$\begin{align*} db &= \frac{1}{m} \sum_{i=1}^{m}dz^{(i)} \\ &= \frac{1}{m} \cdot np.sum(dZ) \end{align*}$$
注： np.sum(dZ)是调用python中numpy库的一个函数，其功能是将矩阵的所有元素相加。

7、向量化之后的实现逻辑回归过程

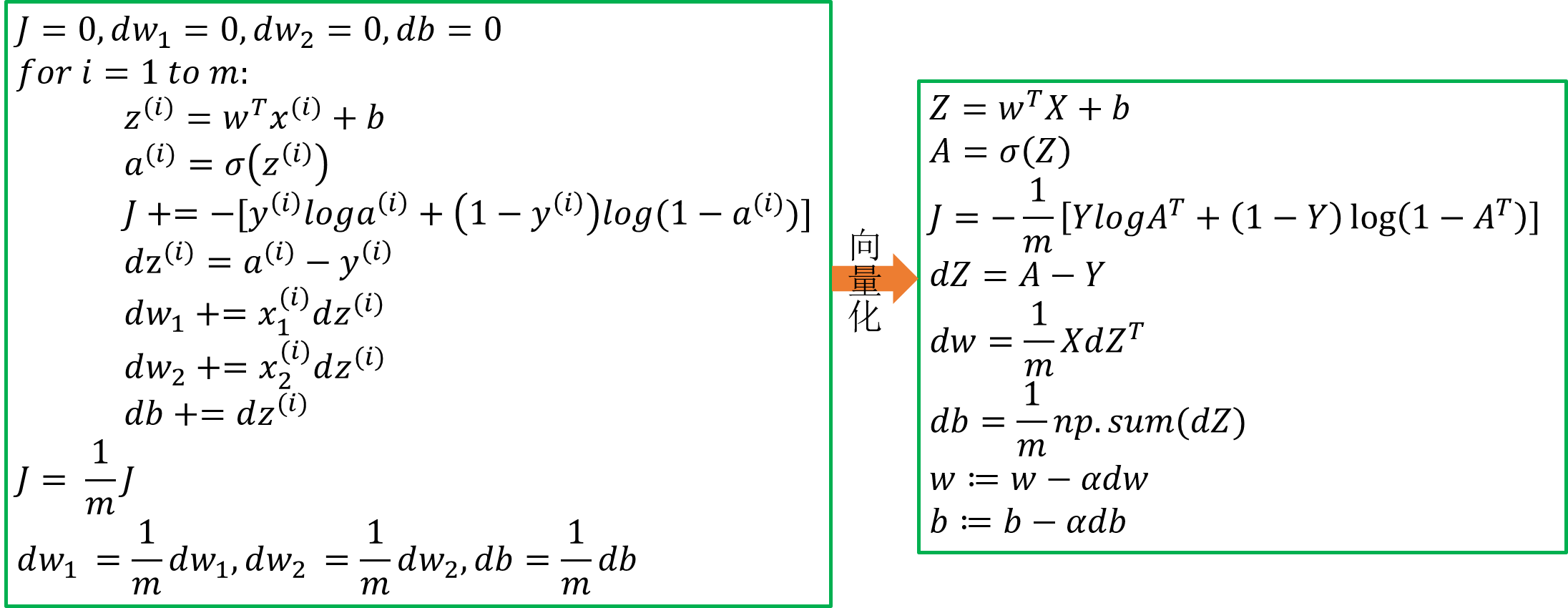
注：这里展示的伪代码都是一次迭代过程，若需要多次迭代，则需要在外层增加for循环。

参考文献：
1、本内容主要来自于coursera上的dl视频，在此加上一些自己的看法和理解。
2、一步步手写神经网络