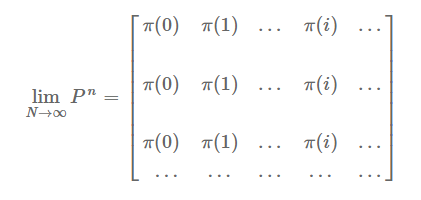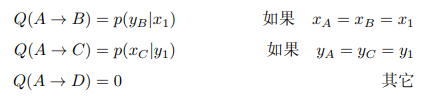蒙特卡洛采样与Gibbs采样

采样

采样问题指的是给定一个特定的概率分布p(z)，得到一批符合这个概率分布的样本点。

采样的方法有很多，MCMC是其中的一类方法，意思是利用Mento Carlo和Markov Chain完成采样。

当然，要完成对各种分布的采样，有一个默认的假设，就是我们已经能够对均匀分布进行采样了(后面就专指范围为0-1的均匀分布)，也就是编程中通常会用到的伪随机数发生器，在各大编程语言中通常以random命名的模块/方法出现。

蒙特卡洛思想

蒙特卡罗方法是一种通过在一定范围内均匀随机抽样来得到某个结果的计算方法。方法的大致思路框架是：

• 针对计算问题选定抽样范围
• 在范围内进行随机抽样
• 根据问题定义，计算一些必要的样本统计值（或者说是对样本进行归类）
• 整合这些统计值，得到最终结果

示例

在正方形中作一个内切圆，随机抽样一些点，记在内切圆中的点的数量为c，所有点的数量为n。那么c和n的比例就是内切圆和正方形的比例，即：
$\frac{\pi r^2}{(2r)^2}=\frac{c}{n} \rightarrow \pi = \frac{4c}{n}$

val n = 100000 * slices // slice是控制抽样量的参数
val count = sc.parallelize(1 to n, slices).map { i =>
  val x = random * 2 - 1 // 长度坐标范围-1~1
  val y = random * 2 - 1 // 宽度坐标范围-1~1
  if (x*x + y*y < 1) 1 else 0 //区分出落在圆圈中的点。圆圈半径为1，所以点到圆心距离小于1
}.reduce(_ + _) // 统计点的数量
println("Pi is roughly " + 4.0 * count / n)

马尔科夫链

想象一个国家，其城市人口和农村人口会每年发生一次迁移，并且迁移概率是固定的。假设每年城市迁农村的概率是3%，农村迁城市的概率是5%。如果某一年，城市和农村的人口分别是2000和14000，那么下一年的人口分布是怎么样的？我们可以用如下的矩阵计算表示：

$[2000\ 14000] * \left [\begin{matrix} 0.97 & 0.03\\ 0.05 & 0.95 \end{matrix} \right ]=[2640\ 13360]$

而作为一个个体，其实是在不同的状态（农村或城市）之间跳转，比如t=1时，是农村人，t=2时，是城市人。马尔可夫链就是生成这样一段状态序列的随机过程，其中城市和农村互相流动的矩阵，叫做迁移矩阵。马尔可夫链的这个随机过程满足马尔科夫性质，也就是某一个状态的值，只跟前一个状态相关。用公式表示就是：

$P(Xn|Xn−1,…,X0)=P(Xn|Xn−1)$

而迁移矩阵的每一个元素其实就对应着一个条件概率值。所以后面会同时用P(j|i)和 $P_{ij}$这两种写法来代表迁移矩阵的某一项。

现在回头来看刚才那个例子。当状态迭代到一定程度之后，会发现，城市和农村的人数都固定了，城市人数是10000，农村人数是6000。而且用任意一个总人口为16000的状态作为初始状态，最后的结果都是这个。对于个体来说，这就是个体会留在农村还是城市的概率分布，也就是留在城市和农村的概率比为5:3，这个分布也叫马尔可夫链的平稳分布。简单起见，我们这里就不加证明地简单描述下马尔可夫链的收敛性质（严谨的说，需要有一些前提条件才能保证必然收敛，不过前提条件不满足的情况不常见，所以就不增加解释成本了）：

• 马尔科夫链收敛于平稳分布π，使得对于迁移矩阵P，π是方程πP=π的唯一解。把这个解用向量方式表示，就是该分布在各个取值上对应的概率，即π= $[π(0),π(1),…π(i),…],∑iπ(i)=1$
• 迁移矩阵P经过反复迭代之后本身也会收敛(每列结果相同)，才能满足平稳分布的要求，即:

MCMC

既然马尔科夫链可以收敛于一个平稳分布，如果这个分布恰好是我们需要采样的分布，那么当马尔科夫链在第n步收敛之后，其后续不断生成的序列 $Xn,Xn+1,…$就可以当做是采样的样本。这就是MCMC方法的基本思想。那么如何找到符合条件的迁移矩阵P？

学者们在研究之后提出了细致平稳条件，满足细致平稳条件的马尔科夫链可以收敛到指定的概率分布。细致平稳条件即对一个分布π，如果迁移矩阵P对任意i,j满足 $π(i)Pij=π(j)Pji$，那么π就是这个马尔科夫链的平稳分布。不加证明的通俗理解这个条件的含义，就是状态i转移到状态j的量被j到i的量给抵消了，就比如上一节的例子中，有多少城市人流动到农村，就会有相同数量的人从农村流动到城市。

有了这个条件之后，就要想办法找一个满足这个条件的迁移矩阵。先从一个随便的普通迁移矩阵开始，为了简单起见，可以认为我们用了一个均匀分布的迁移矩阵，即每一项Pij的值都是一样的。这个矩阵当然不满足细致平衡条件：

$π(i)P_{ij}≠π(j)P_{ji}$

当然，如果直接让 $P_{ij}=π(j),P_{ji}=π(i)$的话，上面的等式就成立了。但是如果直接这样构造马尔科夫链，显然是不具有收敛性质的。不过我们可以借鉴这个思路，引入aij使得 $π(i)P_{ij}a_{ij}=π(j)P_{ji}a_{ji}$，并且让 $a_{ij}=π(j)P_{ji}$，那么记 $Q_{ij}=P_{ij}a_{ij}$，即由P和a结合的新马尔科夫链Q也能满足条件。这个时候，计算转移概率时，对Q的采样可以处理成先对P采样（可以用刚才说的均匀分布，或者正态分布也有成熟的方法，即box muller变换），然后把a当成一个接受率的概念，随机采样之后看是否到达 $a_{ij}=π(j)P_{ji}$的条件，满足条件说明可以转移。梳理一下这个流程，可以得到我们的MCMC算法：

简单解释一下。现在我们的目的是要按照转移矩阵Q进行跳转，2.1步代表先用原来的P进行跳转，跳转之后的值假设是y。2.2步的接受率就是将前后两个状态 $i=x_{t}$和 $j=y$代入 $a_{ij}=π(j)P_{ji}$，2.3步采样随机数决定是否跳转。

Metropolis Hastings算法

上面的MCMC方法已经可以工作，但是实际中使用的Metropolis Hastings算法是基于上面的算法做了改进的。需要改进的点就在于接受率a如果偏小，那么马尔科夫链很容易拒绝跳转，导致收敛速度慢。实际上我们可以把a放大，只要保证对任意i,j， $max(a_{ij},a_{ji})=1$即可。我们要计算的接受率是 $a_{ij}$，如果 $a_{ij}$更大，那么把新的 $a_{ij}$放大到1即可，如果 $a_{ij}$比较小，那么两边同时除以原来的 $a_{ji}$，使得新的 $a_{ji}$放大到1即可。于是我们得到了Metropolis Hastings算法：

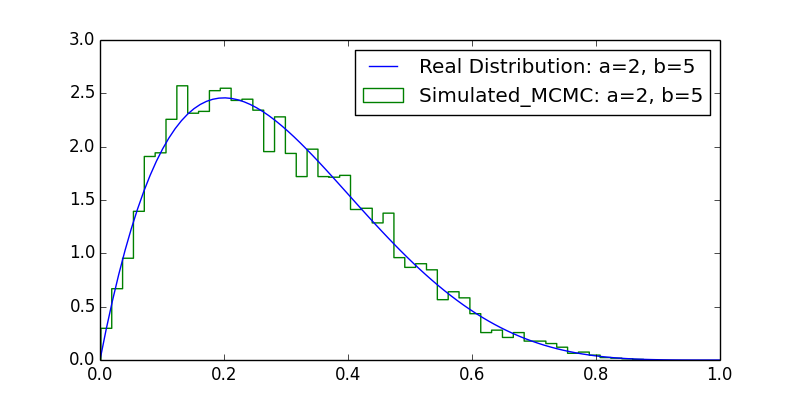
我们尝试模拟一下beta分布。以下代码基于引用1改写：

# -*- coding: utf-8 -*-

import random
import numpy as np
import pylab as pl
import scipy.special as ss

# 完整的beta分布概率密度函数
def beta(a, b, i):
    e1 = ss.gamma(a + b)
    e2 = ss.gamma(a)
    e3 = ss.gamma(b)
    e4 = i ** (a - 1)
    e5 = (1 - i) ** (b - 1)
    return (e1/(e2*e3)) * e4 * e5

# beta分布概率密度函数去掉前面的常数项之后的形式
def beta_s(a,b,i):
    return i**(a-1)*(1-i)**(b-1)

# mcmc模拟
def beta_mcmc(N_hops,a,b):
    states = []
    cur = random.uniform(0,1) # 初始化状态
    for i in range(0,N_hops):
        states.append(cur)
        next = random.uniform(0,1) #从原来的迁移矩阵P采样，这里假设P是一个基于均匀分布的迁移矩阵
        #计算接受率，因为beta分布的常数项会抵消，所以用不带常数项的形式，能大幅提速。而且P是均匀分布，所以也相互抵消了
        ap = min(beta_s(a,b,next)/beta_s(a,b,cur),1) 
        if random.uniform(0,1) < ap: #随机采样决定是否跳转
            cur = next
    return states[-10000:] #取最后的一部分状态，保证已经收敛

#可视化
def plot_beta(a, b):
    Ly = []
    Lx = []
    i_list = np.mgrid[0:1:100j]
    for i in i_list:
        Lx.append(i)
        Ly.append(beta(a, b, i))
    pl.plot(Lx, Ly, label="Real Distribution: a="+str(a)+", b="+str(b))
    pl.hist(beta_mcmc(1000000,a,b),normed=True,bins=50, histtype='step',
            label="Simulated_MCMC: a="+str(a)+", b="+str(b))
    pl.legend()
    pl.show()

pl.rcParams['figure.figsize'] = (8.0, 4.0)
plot_beta(2, 5)

输出的可视化结果为：

Gibbs采样

Gibbs Sampling需要应用在至少二维的数据上，所以下面先以二维的情况为例。

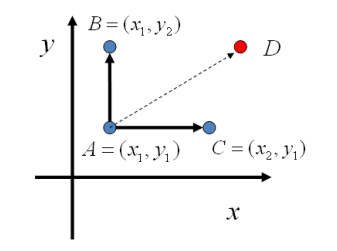
当数据是二维的时候，我们需要模拟的是一个联合概率分布 $P(x,y)$。当状态的跳转仅仅是在一个维度上变，另一个维度不变的时候（假设y变，x不变为恒定值x1），如果用条件概率 $P(y|x1)$来作为这些点之间的转移概率，这种情况下就能满足细致平稳条件。简单的证明一下，假设 $A(x1,y1),B(x1,y2)$是两个点，这两点之间做跳转，那么A和B对应的迁移概率分别是 $P(y2|x1)和P(y1|x1)$，于是有：

$P(A)P(y2|x1)=P(x1,y1)P(y2|x1)=P(x1)P(y1|x1)P(y2|x1)=P(x1,y2)P(y1|x1)=P(B)P(y1|x1)$
所以我们的迁移矩阵可以用上面的方法定义，平面上马氏链转移矩阵Q：

于是，我们可以如下构造平面上任意两点间的转移概率矩阵：

举一个简单的例子。假设我们需要模拟的变量的维度是性别和居住地（城市或农村），相当于在马尔科夫链那节的例子增加一个性别维度，迁移矩阵记为Q，概率分布记为p，那么Q(男性城市人|男性农村人)=p(城市人|男性)。

根据上面构造的迁移矩阵，二维情况下的GS算法就出来了：

也就是说，如果要从 $(x_{0},y_{0})$跳转到 $(x_{1},y_{1})$，中间会经过一层 $(x_{0},y_{1})$的跳转，每次的跳转先在一个维度上变化。

当然在实际应用中，无论是MH算法还是GS算法，一般都要应用在多维数据上。我们把上述二维的情况推广到多维，就是完整的GS算法：

可以看到，多维的情况下，每一次采样还是只能移动一个维度，其余的n−1个维度都作为条件。

相比MH算法，GS算法每次跳转都没有被拒绝的可能，所以一般会说GS算法是MH算法的一个特例，即接受率为1的MH算法。

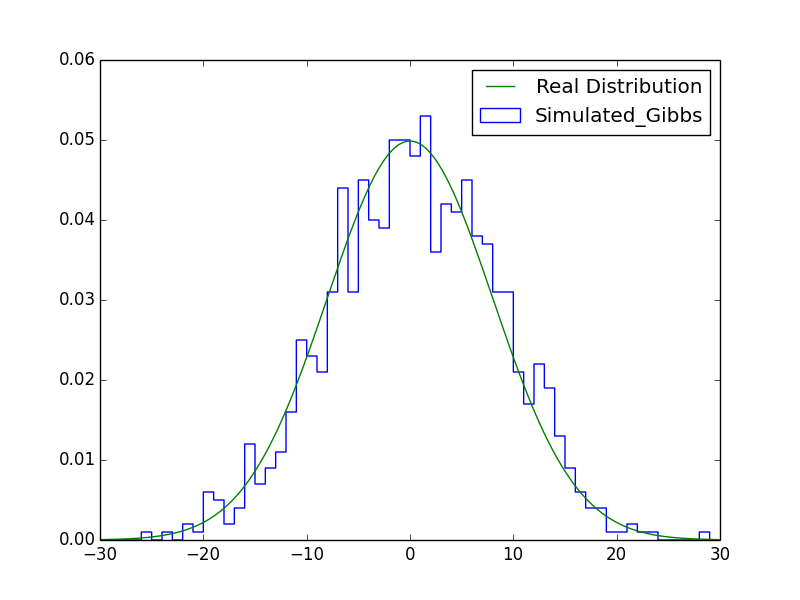
最后，我们用Gibbs Sampling来模拟一下二维正态分布。二维正态分布的两个维度本身就是正态分布，假设 $X∼N(μ_{x},s_{x}^{2})，Y∼N(μ_{y},s_{y}^{2})$，X和Y的相关系数为ρ，那么可以推导出条件分布(推导过程见参考资料3):
$(Y|X=x)∼N(μ_{y}+ρ\frac{s_{y}}{s_{x}}(X−μ_{x}),s_{y}^{2}(1−ρ^{2}))$

根据以上条件概率的公式，就可以写出相应的代码了：

# -*- coding: utf-8 -*-

import pylab as pl
import numpy as np
import math

# x和y两个维度的均值都是0

sx = 8 # x维度正态分布的标准差
sy = 2 # y维度正态分布的标准差
cor = 0.5 # x和y的相关系数

# x维度的概率密度函数
def pdf_gaussian_x(x):
    return (1 / (math.sqrt(2 * math.pi) * sx)) * math.exp(-math.pow(x, 2) / (2 * math.pow(sx, 2)))

# 条件分布 p(x|y)
def pxgiveny(y):
    return np.random.normal(y * (sx/sy) * cor, sx * math.sqrt(1 - cor * cor))

# 条件分布 p(y|x)
def pygivenx(x):
    return np.random.normal(x * (sy/sx) * cor, sy * math.sqrt(1 - cor * cor))

def gibbs(N_hop):

    x_states = []
    y_states = []
    
    #状态随机初始化
    x = np.random.uniform()
    y = np.random.uniform()
    
    for _ in range(N_hop):        
        x = pxgiveny(y) #根据y采样x
        y = pygivenx(x) #根据x采样y
        x_states.append(x)
        y_states.append(y)

    return x_states[-1000:], y_states[-1000:]

def plot_gibbs():
    x_sim, _ = gibbs(100000)
    
    x1 = np.arange(-30, 30, 1)
    pl.hist(x_sim, normed=True, bins=x1, histtype='step', label="Simulated_Gibbs")
    
    x1 = np.arange(-30, 30, 0.1)
    px1 = np.zeros(len(x1))
    for i in range(len(x1)):
        px1[i] = pdf_gaussian_x(x1[i])
    
    pl.plot(x1, px1, label="Real Distribution")
    pl.legend()
    pl.show()

plot_gibbs()

作图部分为了兼顾方便和清晰，只基于一个维度做了可视化，结果如下图：

应用场景

基于MCMC的采样方法主要有两类应用场景。第一类是应用于求函数的期望值，或者说是积分问题。另一类是求解最优化问题。

积分问题

把采样用在积分计算上，一个应用场景就是用在贝叶斯估计中。首先根据贝叶斯公式，写出后验概率：

$P(θ|X)∝P(X|θ)P(θ)$
在这里，似然P(X|θ)是θ的函数，P(θ)作为先验代表了θ的概率密度。一般情况下我们用MLE和MAP求解模型参数，但是也有一些情况下我们需要求解的是参数的期望值（比如后验分布太复杂，很难求最大值），这个时候求解的内容就是：

$E[θ]=∫θP(θ|X)dθ$
事实上我们利用这个思路还可以直接进行预测，也就是求P(y|X)：

$P(y|X)=E[f(θ)]=E[P(y|θ)]=∫P(y|θ)P(θ|X)dθ$
综上，我们可以把问题重新描述如下：

假设Z是一个连续随机变量(离散的情况类似)，其概率密度函数为p(z)，现在需要计算函数f(z)的期望值，即

$E[f(z)]=∫f(z)p(z)dz$
那么如果我们能根据p(z)采样出来一堆点z(1),z(2),…z(n)，那么我们用这些点代入函数求均值，随着采样的点增多，得到的结果就越来越逼近理论结果：

$E[f(z)]=\lim_{N→∞} \frac{1}{N} \sum_{1}^{N}f(z^{(t)})$

最优化

最优化问题就是求解函数的最小/最大值的问题。最优化的方法有很多，跟MCMC有关的最优化方法就是模拟退火法。模拟退火（Simulated Annealing）是一种通用的最优化方法，理论上可以做到全局最优化。当然实际使用中，如果要保证达到全局最优，那么退火速度将会慢到无法接受，所以实际使用中不能保证全局最优，不过也比一般的贪心方法要效果好。

上面所谓的贪心方法指的就是爬山法。爬山法会随机搜索相邻状态，并且向最优的状态移动，直至相邻状态没有更好状态为止。爬山法作为纯贪心方法很多时候由于起始点不够好，只能找到局部最优解（与梯度下降还是不一样的，梯度下降是根据梯度方向调整，爬山法是随机采样），而模拟退火的意思是，如果遇到更坏的情况，那么会有一定概率接受，这样一来就能跳出局部最优解。

然而这只是SA算法的大体思想，按照这个大体思想也能看懂代码。但如果要探究到底是按照什么原理去接受所谓的更坏情况，就要跟MCMC扯上关系了。假设我们需要最小化的函数是f(x)，SA算法将其置于Gibbs分布（也叫Boltzmann分布）中，即：

$P(x)=\frac{1}{Z}e^{\frac{−f(x)}{T}}$
这里Z是规范化项，T是参数。这个分布的特性是，当T很大的时候，接近均匀分布，而T很小的时候，函数−f(x)的最大值会被无限放大，导致在相应状态下的概率接近1，即T→0，P(x=argminxf(x))=1。这也就是说，如果我们能在T很小的情况下采样得到x，那么这个对应的函数值基本上可以断定是函数最小值。不过当T很小的时候，由于分布过于陡峭，所以用MH算法得到的接受率往往会非常小，导致一直拒绝跳转。所以我们可以从T比较大的情况开始采样，比如一开始根据T1和初始点x0采样得到x1，然后更新T缩小到T2，这个时候根据x1的值为出发点继续采样，得到x2，如此循环，每一步的采样结果为下一步减少了范围，使得采样过程保持稳定，最后就能逐步的把T减小到一个很小的值。

下面就通过代码实现来计算一个函数的最小值：

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import random
import math

# 目标函数，有两个变量。为了让收敛过程看起来清晰一点，找了一个复杂一点的函数
def f(x):
    x1 = x[0]
    x2 = x[1]
    obj = x1**2 + x2**2 - 0.1*math.cos(6.0 * math.pi * x1) - 0.1*math.cos(6.0 * math.pi * x2)
    return obj


x_start = [1, -.5] # 初始点
t_start = 1 #起始温度参数
t_end = 0.02 #结束温度参数
n = 50 #温度变化分几轮做完
frac = (t_end/t_start)**(1.0/(n-1.0)) #每次温度缩小系数

#记录每一次温度变化之后的最终采样结果
x = np.zeros((n+1,2))
x[0] = x_start

# 每轮mcmc采样中新一轮跳转状态
xi = np.zeros(2)
xi = x_start

# 每轮mcmc采样中当前最好状态
xc = np.zeros(2)
xc = x[0]

# 对应函数值的当前最好状态和每轮状态
fc = f(xi)
fs = np.zeros(n+1)
fs[0] = fc

t = t_start
for i in range(n):
    for j in range(200): # MCMC跳转200次
        
        # 在上一轮采样结果的附近采样
        xi[0] = random.random() - 0.5 + xc[0]
        xi[1] = random.random() - 0.5 + xc[1]

        # 根据gibbs分布计算接受率
        a = math.exp(-(f(xi)-fc)/t)
       
        # 如果采样满足接受率条件，或者本来就取到了更小的值，就接受跳转
        if (random.random() < a) or (f(xi) < fc):
            xc[0] = xi[0]
            xc[1] = xi[1]
            fc = f(xc)
         
    # 存储每轮MCMC采样结果
    x[i+1][0] = xc[0]
    x[i+1][1] = xc[1]
    fs[i+1] = fc
    
    # 减小温度参数
    t = frac * t
   
# 可视化
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(fs,'r.-')
ax1.legend(['Objective'])

ax2 = fig.add_subplot(212)
ax2.plot(x[:,0],'b.-')
ax2.plot(x[:,1],'g--')
ax2.legend(['x1','x2'])

plt.show()

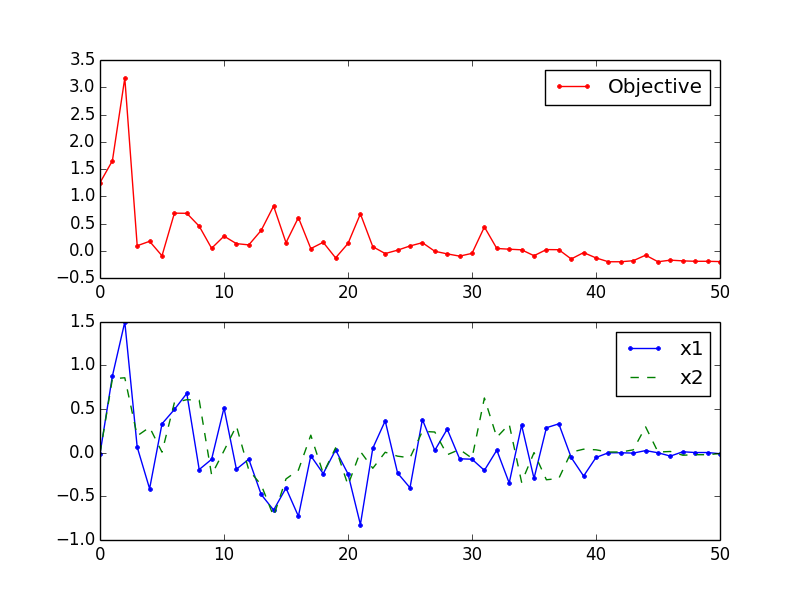
通过可视化输出可以看到，目标函数值虽然在收敛过程中会出现变大的情况，但是最终还是落到最小值，而相应的变量也逐渐收敛：

除了用在通用的最优化方法上面，MCMC也可以应用在具体的问题上，比如在The Markov Chain Monte Carlo Revolution一文中，就提到过一个破译凯撒密码的例子。通过随机生成解密key，根据解密key替换原文后的评估分数决定是否跳转（跳转就是交换任意两个字母的替换规则），最后得到收敛的结果就是正确的解密key。

引用

1、My Tryst With MCMC Algorithms
2、LDA数学八卦
3、Penn State University STAT414 online course
4、MCMC方法小记
5、 一个MCMC的实例