变分自编码器(VAE)

版权声明：本文为博主原创文章，未经博主允许不得转载。作为分享主义者(sharism)，本人所有互联网发布的图文均采用知识共享署名 4.0 国际许可协议(https://creativecommons.org/licenses/by/4.0/)进行许可。转载请保留作者信息并注明作者Jie Qiao专栏:http://blog.csdn.net/a358463121。商业使用请联系作者。 https://blog.csdn.net/a358463121/article/details/79543198

变分自编码器(VAE)

从EM到变分推断

我们假设有一个隐变量z，我们的样本 $x^{( i)}$是从 $p_{\theta }( x|z)$中产生，因为有隐变量的存在，通常 $p_{\theta }( x) =\int p_{\theta }( z) p_{\theta }( x|z) dz$的边缘分布是没法算的。

所以传统来说，我们会构造出一个下界：
$\begin{aligned} \log p( x) & =\underbrace{E_{z\sim q( z)}(\log p( x ,z)) -H( q)}_{ELOB} +KL( q( z) ||p( z |x)) \end{aligned}$
因此当我们最大化下界（ELOB）时，就相当于在最小化 $KL( q( z) ||p( z |x))$

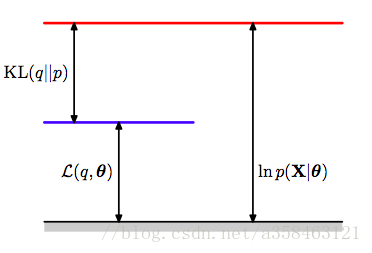
而EM算法，就是通过精心选择这个下界中的q，从而使得下界最大化，也就是计算 $q( z) =p( z|x)$来近似该模型的似然度。进一步可以参考我之前写的文章《带你理解EM算法》

然而如果我们令 $q( z) =p( z|x) =\frac{p_{\theta }( x|z) p_{\theta }( z)}{p_{\theta }( x)}$也是不可计算的呢，比如你的z有很多很多维，那么你在算那个期望的时候就会出现一堆积分，这是非常难算的。

此时我们可以使用变分推断的方法，那就是，我们不直接令 $q( z) =p( z|x)$了，而是选一个相对简单的分布 $q(z)$去近似 $p( z|x)$，（注意，这个q不一定是q(z)还可以是q(z|x)，这种情况称为amortized variational），这个“近似”的数学形式写作 $\min_q KL(q(z)\| p(z|x))$或 $\min_q KL(q(z|x)\| p(z|x))$。那么简单的q怎么来？最常用的就是对q作平均场(mean-field)假设，即，我们可以认为：
$q(\mathbf{z}) =\prod _{i} q_{i}( z_{i})$
这个假设的意思是，虽然你的z有很多维，但是他们都是相互独立的，也就是说，你算很多很多积分的时候，每个 $z_{i}$可以分别积分，所以一个联合积分的问题就简化成了仅需一个积分的问题，于是我们在优化ELOB的时候，只需分别优化 $q_{i}$就可以了。将平均场假设代进ELOB中，化简可以得到
$\begin{aligned} ELOB & =\int _{z_{j}} q_{j}( z_{j})\left[\underset{z_{i\neq j}}{\int \dotsc \int } q( z)\log p( x,z) dz_{i}\right] dz_{j} -\sum _{i}\int _{z_{i}} q_{i}( z_{i})\log q_{i}( z_{i}) dz_{i}\\ & =\int _{z_{j}} q_{j}( z_{j}) E_{i\neq j}[\log p( x,z)] dz_{j} -\int _{z_{j}} q_{j}( z_{j})\log q_{j}( z_{j}) dz_{j} -\underbrace{\sum _{i\neq j}\int _{z_{i}} q_{i}( z_{i})\log q_{i}( z_{i}) dz_{i}}_{Const\ for\ j}\\ & =\int _{z_{j}} q_{j}( z_{j})\log\frac{E_{i\neq j}[\log p( x,z)]}{q_{j}( z_{j})} dz_{j} -\underbrace{\sum ^{M}_{i\neq j}\int _{z_{i}} q_{i}( z_{i})\log q_{i}( z_{i}) dz_{i}}_{Const\ for\ j}\\ & =-KL( E_{i\neq j}[\log p( x,z) ||q_{j}( z_{j})]) +const \end{aligned}$

因为每个 $z_{j}$都是相互独立，于是，只需分别最大化每个 $z_{j}$的ELOB就可以实现ELOB最大化，而其他的项都视作了常数，此时，ELOB就简单地变成了一个负的KL距离，所以，想要最大化这个ELOB，我们只需要令
$q_{j}( z_{j}) =E_{i\neq j}[\log p( x,z)]$
就可以了。这实际上是一个迭代的问题，因为在constant中，包含了其他的项的q，所以，我们只需不断地更新各个元素q的分布直到收敛就可以了。

从变分推断到VAE

但是，如果即使用了平均场假设也没法算，而使用MCMC又太慢怎么办？为了解决这个问题，我们回到最初的那个下界的表达式中

$\begin{aligned} \log p( x |\theta ) & =\underbrace{E_{z\sim q( z)}(\log p( x ,z)) -H( q)}_{ELOB} +KL( q( z) ||p( z |x)) \end{aligned}$
实际上ELOB有几种不同的，但是等价的表达方式：

KL form :
$\mathcal{L}( \theta ;x) =E_{z\sim q( z)}(\log p_{\theta }( x|z)) -KL( q( z) ||p_{\theta }( z))$
Entropy form:
$\mathcal{L}( \theta ;x) =E_{z\sim q( z)}(\log p_{\theta }( x ,z)) -H( q)$
Fully Monte Carlo(FMC) form:
$\mathcal{L}( \theta ;x) =E_{z\sim q( z)}[\log p_{\theta }( x,z) -\log q( z)]$

其中q是一个任意的分布，那么现在，我们令 $q( z) \triangleq q_{\phi }( z|x)$，用KL形式的下界可以得到：
$\mathcal{L}( \theta ,\phi ;x) =E_{z\sim q_{\phi }( z|x)}(\log p_{\theta }( x|z)) -KL( q_{\phi }( z|x) ||p_{\theta }( z))$
现在引入了一个带参数的 $q_{\phi }$来表示这个上界，如果要最大化这个上界，我们只要用梯度上升不断更新参数$\phi $就可以了。一般情况下，KL距离的那一项是有解析解的，所以梯度很好求。然而对第一项求梯度则没那么简单，一个常用的方法是$\nabla {\phi } E{z\sim q_{\phi }( z)}( f( z)) =E_{z\sim q_{\phi }( z)}[ f( z) \nabla {\phi }\log q{\phi }( z)] \simeq \frac{1}{L}\sum ^{L}_{l=1} f\left( z^{l}\right) \nabla {\phi }\log q{\phi }\left( z^{l}\right)$，但是这么做的方差太高。

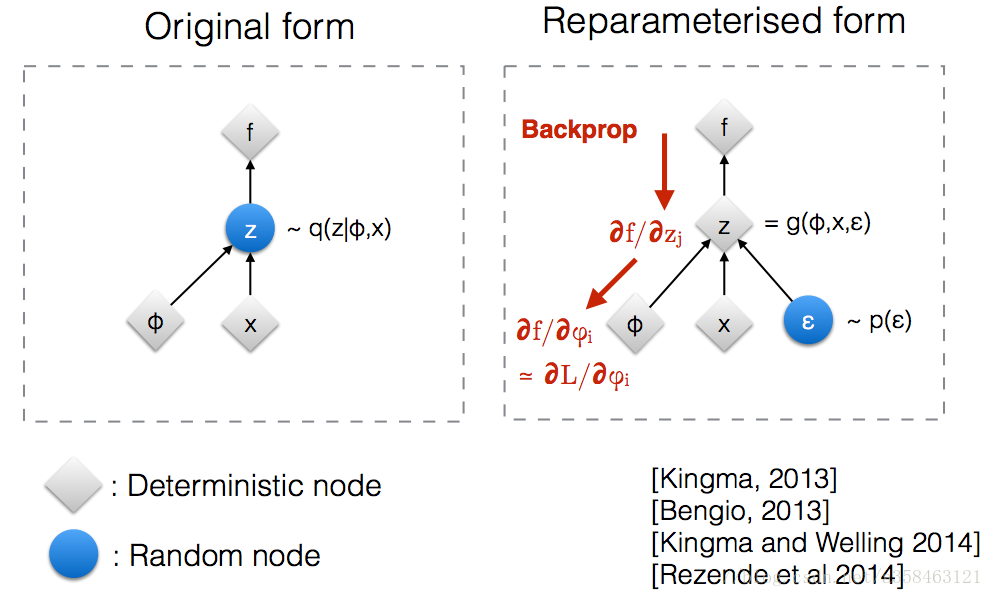
如上图，我们可以用reparameterize trick来解决这个问题，这时z对于x来说就是一个固定的值，只要我们从 $\epsilon$中抽样后，固定住就可以了，设
$z=g_{\phi }( \epsilon ,x) ,\epsilon \sim p( \epsilon )$
其中$\epsilon $是一个已知的简单分布，比如说标准正态分布，次数z的产生就变成了从某个固定的标准分布中采样，于是下界中的期望那一项可以改写成：
$E_{z\sim q_{\phi }( z|x)}(\log p_{\theta }( x|z)) =E_{\epsilon \sim p( \epsilon )}(\log p_{\theta }( x|g_{\phi }( \epsilon ,x))) \simeq \frac{1}{L}\sum ^{L}_{l=1}\log p_{\theta }( x|g_{\phi }( \epsilon ,x))$
于是对于一个样本 $x^{( i)}$的下界可以写作：
$\mathcal{L}\left( \theta ,\phi ;x^{( i)}\right) =\frac{1}{L}\sum ^{L}_{l=1}\log p_{\theta }\left( x^{( i)} |z^{( i,l)}\right) -KL\left( q_{\phi }\left( z^{( i)} |x^{( i)}\right) ||p_{\theta }\left( z^{( i)}\right)\right)$
其中 $z^{( i,l)} =g_{\phi }\left( \epsilon ^{( i,l)} ,x^{( i)}\right) ,\epsilon ^{( l)} \sim p( \epsilon )$
在这里，如果我们用一个MLP来表示 $p_{\theta }$和 $q_{\phi }$和就可以对用这个目标函数求梯度来最大化了，注意产生z的分布 $q_{\phi }$其实是由一个标准正态分布的$\epsilon $和一个用MLP表示的映射函数$g_{\phi } $构成的，所以训练过程实际上是更新$p_{\theta } $和$g_{\phi } $这两个MLP的参数，我们称$p_\theta $为encoder network,$q_{\phi } $为decoder network。而z的产生则是从$p( \epsilon ) $抽一个样本，然后经过一个确定性$g_{\phi }$来产生。

更直观一点，如果我们假设先验分布 $p( z)$, $p( \epsilon )$服从标准正态分布，
$z=q_{\phi }( z|x) =g_{\phi }( \epsilon ,x) =\mu _{\phi }( x) +\Sigma _{\phi }^{1/2}( x) \epsilon$
也就是说， $q_{\phi }( z|x) \sim N\left( \mu _{\phi }( x) ,\Sigma _{\phi }^{1/2}( x)\right)$也是正态分布，不过其参数由x决定。于是对于两个正态分布的KL距离，对于有J个维度的z，我们完全可以算出其解析解：
$\begin{aligned} -KL( q_{\phi }(\mathbf{z} |\mathbf{x}) ||p_{\theta }(\mathbf{z})) & =-KL( N(\mathbf{\mu }_{\phi } ,\mathbf{\sigma }_{\phi }) ||N(\mathbf{0} ,\mathbf{I}))\\ & =\frac{1}{2}\sum ^{J}_{j=1}\left(\left( 1+\log \sigma ^{2}_{j}\right) -\mu ^{2}_{j} -\sigma ^{2}_{j}\right) \end{aligned}$

接下来我们看看这个网络的架构

encoder network将一只喵星人映射成一个均值和一个方差，然后产生一个z样本，通过decoder network再变成一只喵~

然而VAE对比GAN确实存在一些问题。

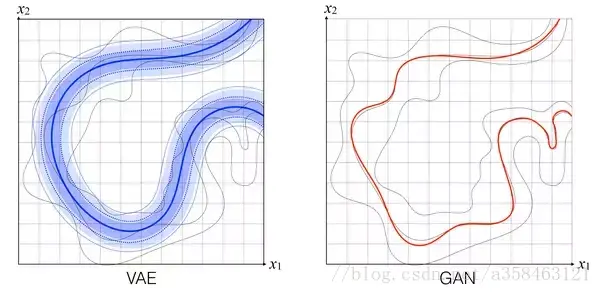
可以看到VAE的“拟合”能力没有GAN的强，VAE会趋于平滑而GAN则不会。而且VAE产生的图像会比较模糊，这似乎所有优化对数似然的目标函数 $KL(p_{data}||p_{model})$都有这问题(《Deep learning》)，这一点，或许与KL距离的性质有关系，可以看我的另外一篇文章，《正向跟反向KL距离到底有什么区别？》

参考资料

Auto-encoding variational bayes

Tutorial on variational autoencoders

How does the reparameterization trick for VAEs work and why is it important?

Variational Autoencoders Explained
Deep learning

徐亦达机器学习课程

带你理解EM算法

作为分享主义者(sharism)，本人所有互联网发布的图文均遵从CC版权，转载请保留作者信息并注明作者Jie Qiao专栏:http://blog.csdn.net/a358463121，如果涉及源代码请注明GitHub地址：https://github.com/358463121/。商业使用请联系作者。