聚类属于无监督学习。在之前的学习中,都是监督学习。监督学习与无监督学习的最大区别为训练数据集的特点,在监督学习中,训练集是有标签的,我们根据这些有标签的数据,训练出模型,输出相应的值。而在无监督学习中,我们的数据集没有标签,我们需要使用机器学习算法寻找出数据集中的内在结构。无监督学习的数据集如下所示
训练的数据集可以写成只有一直到
,没有任何的标签
。上图中的数据可以看作两个分开的点集(称为簇),能找出这些点集的算法就称为聚类算法。
1k-均值算法
k-均值算法是最普及的算法,该算法接受一个未标记的数据集,然后将数据集聚类成不同的类。k-均值算法是一种迭代算法,假设我们将数据聚类成n个组,那么步骤如下:
首先随机选择K个随机点,称为聚类中心(cluster centroids)。对于数据集中的每个数据,计算他们与这些K个聚类中心的距离,然后将其与之关联起来(可认为每个组即为一个类,关联即属于该类),将所有与这个聚类中心关联的点归为一类。
下一步是重新设置聚类中心,计算每一个组的平均值,将聚类中心的坐标移动到平均值的位置。
然后不断进行这两个步骤的迭代,直到聚类中心点不再变化。
迭代10次,用来表示聚类中心,用
来存储与第
个实例数据最近的聚类中心的索引,k-均值算法的伪代码如下所示:
Repeat{
for =1 to
:=index (from 1 to
) of cluster centroid closest to
for =1 to
:=average (mean) of points assigned to cluster
}
就如上述所讲,该算法分为两个步骤,第一个for循环是计算训练集中每一个样例,看其属于哪个类。第二个for循环是聚类中心的移动,即计算属于该组的点的平均值。
K-均值算法也可以便利的将数据分为不同的组,即使在没有非常明显区分的组群的情况也可以。如下图所示,下图所示的数据集包含身高和体重两项特征构成的,利用K-均值算法将数据分为三类。
2优化目标
我们之前的机器学习都有一个优化目标,聚类算法也一样。K-均值最小化的问题就是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,因此k-均值的代价函数(又称畸变函数 Distortion function)为
其中上式的 代表与
最近的聚类中心点。优化目标便是找出使得代价函数最小的
和
之前的k-均值的迭代算法第一个循环是用于减小
引起的代价(也就是将训练数据集归到某个组),第二个循环则是用于减小
引起的代价。迭代的过程一定是每一次迭代都是在减小代价函数,不然就会出错。
3随机初始化
之前在运行k-均值算法之前,我们一开始是选择随机的聚类中心,其实k-均值算法的效果与聚类中心有很大的关系。在运行k-均值算法之前,我们要随机的初始化所有的聚类中心。步骤如下
1.我们应该选择,即聚类中心点的个数要小于所有训练集实例的数量
2.随机选择个训练实例,然后令
个聚类中心分别与这
个训练实例相等。也就是随机选择
个训练集中的数据作为聚类中心。
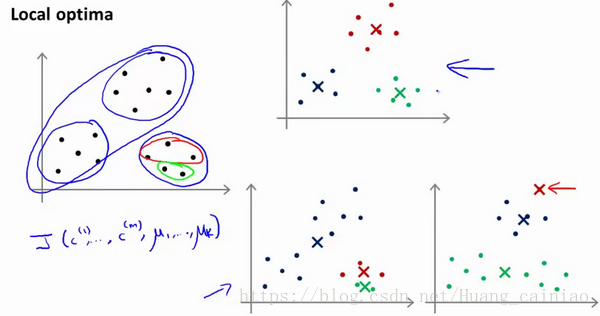
如果执行上诉步骤,那么就会出现问题。我们随机选的聚类中心不好怎么办?如下所示
上图可以看出,随机选择不同的聚类中心就会出现不同的结果,结果有符合预期的也有不符合的。为了解决上诉问题,我们需要多次运行K-均值算法,每次运行之前都进行随机初始化,最后再比较多次运行的结果,选择代价函数最下的那次。但是这种方法在K较小时是可行的(2-10),但是如果K较大,那么这么做不仅效率低,而且也没有较明显的改善。
4选择聚类数
其实选择聚类数没有真正的标准,通常是针对不同的问题,人工进行选择。选择的时候我们考虑使用K-均值算法聚类的目标是什么,然后根据这个目标进行选择聚类的个数。
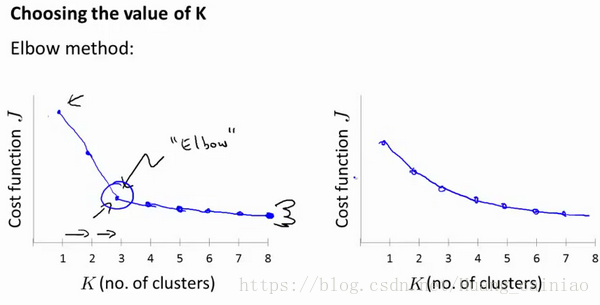
当选择聚类数目时,有可能会用到一个方法叫做"肘部法则"。关于“肘部法则”,我们所需要的时改变K值,也就是聚类的数目,然后算出选择这K个聚类的代价函数。
你会得到上述的左边的图,在某个点中(其实可以称为拐点),代价函数会剧烈的下降,然后变化的很缓慢,所以选择该点作为聚类数目K。但是实际值大部分情况是上述右边的图,那么这时候肘部法则就不管用了.。所以实际过程中还是人工选择具体的聚类数目。
5聚类相关资料
1相识度/距离计算
(1). 闵可夫斯基距离Minkowski/(其中欧式距离:)
(2). 杰卡德相似系数(Jaccard):
(3). 余弦相似度(cosine similarity):
n 维向量x 和y 的夹角记做θ ,根据余弦定理,其余弦值为:
2.聚类的衡量指标
(1). 均一性:p
类似于精确率,一个簇中只包含一个类别的样本,则满足均一性。其实也可以认为就是正确率(每个聚簇中正确分类的样本 数占该聚簇总样本数的比例和)
(2). 完整性:r
类似于召回率,同类别样本被归类到相同簇中,则满足完整性;(每个聚簇中正确分类的样本数占该类型的总样本数比例的和)
(3). 轮廓系数
样本i 的轮廓系数:
簇内不相似度:计算样本 到同簇其它样本的平均距离为
,应尽可能小。
簇间不相似度:计算样本 到其它簇
的所有样本的平均距离
,应尽可能大。
轮廓系数值 越接近1表示样本
聚类越合理,越接近-1,表示样本
应该分类到另外的簇中,近似为0,表示样本
应该在边界上;所有样本的 的均值
被成为聚类结果的轮廓系数。