导数的应用和曲线的凹凸性：

导数的应用：

这块为大家介绍一下导数的应用，导数可以判断一个函数的单调区间，也可以判断函数的凹凸性。

函数的单调性：

这张图上介绍了导数的第一个应用，用导数判断一个函数的单调性非常容易，就是满足以上条件 y=f（x）这个函数求导，如果他的导数大于0那么他就单调递增，反之单调递减。

图中有些专业术语我们好像不熟悉了，我来回顾下：

1. 开区间（）：在一个指定的范围内不包含两边的端点元素的话就是开区间

2. 闭区间 [] ：在一个指定的范围内包含两边的端点元素的话就是闭区间

开元闭方，闭包开不包（开区间用圆括号表示，闭区间用方括号表示，闭区间包含端点，开区间不包括）

举个栗子：

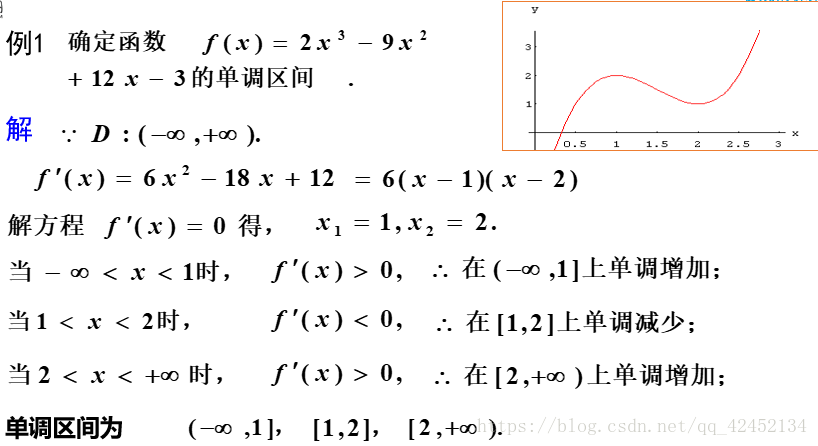
在这个图中我们就可以通过调用一阶导来判断这个函数的单调性，首先把公式求导： $f(x) = 2x^{3} - 9x^{2} +12x -3$

求导得 : ${f}'(x) = 6x^{2} - 18x + 12 = 6(x-1)(x-2)$

接下来我们很容易就能看出y的取值正负了

当 $-\infty$ < x < 1 的时候，把它代入导数化简的公式里面，最后 ${f}'(x)>0$ , 所以在这个区间上是递增

当 1 < x < 2 的时候，把它代入导数化简的公式里面，最后 ${f}'(x)<0$ , 所以在这个区间上是递减

当 2 < x < $\infty$ 的时候，把它代入导数化简的公式里面，最后 ${f}'(x)>0$ , 所以在这个区间上是递增

因此我们通过求出导数的取值正负就可以得出这个函数的单调区间， ${f}'(x)$ 为正则递增，为负递减。

曲线的凹凸性：

首先我们大概理解下什么是凹凸性，凹凸性救赎描述一个曲线弯曲程度的东东，具体怎么描述，咱们来看一下：

在这个图中我们给出了两条函数线，第一个叫下凸，也叫上凹；第二个叫上凸也叫下凹，在这里我们应该通过以上的公式来判断凹凸：

1. 第一个公式中 $f\left ( \frac{x_{1}+x_{2}}{2} \right )< \frac{f(x_{1})+f(x_{2})}{2}$ 如果这个不等式成立的话就说明这个函数线上的(x1,f(x1))和(x2,f(x2))两点间的中点小于这两点函数间的中点，那么就说明这个函数是下凸的。

2. 第二个公式中 $f\left ( \frac{x_{1}+x_{2}}{2} \right )> \frac{f(x_{1})+f(x_{2})}{2}$ 不等式成立就说明他是上凸。

不过这种方法虽然能判断，但是好像判断起来很不实用，接下来咱们就安利一下二阶导数的应用了：

在这里我们如果想要判断一个函数在一个区间内的凹凸性的话，直接对他求二阶导就好啦，二阶导大于0那就是凹的，反之就是凸的，在这里我们有的时候可能不明白为什么x1要等于0 ，x2等于 2/3，这是因为如果我们想要对这个函数求导，那么他都是趋近0的，所以我们要找到y的0点，所以我们把只要能让y=0的x值都带进去就可以啦。因此我们得出结论：

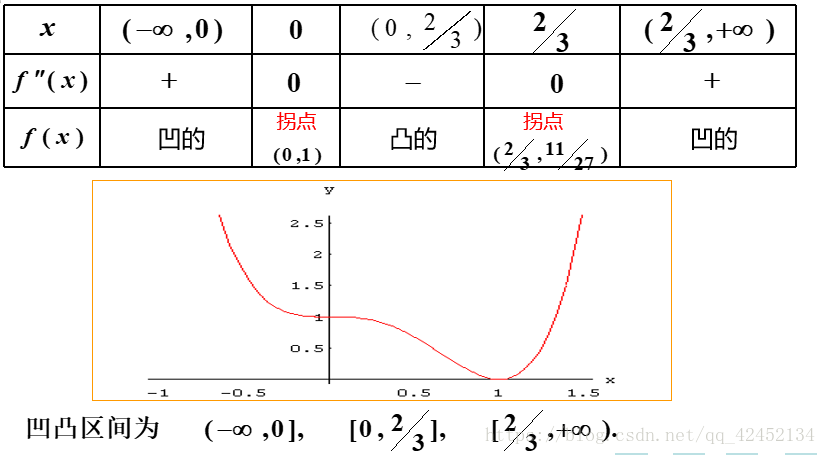
在这个图中我们又发现了利用这个方法也能求出一个函数的拐点：

1. 拐点：拐点就是在一个函数线上凹线和凸线的交界处。

2. 当二阶导数大于0的时候函数是凹，因为二阶导数大于0的时候他没有最大值，但是有最小值所以他是凹的。

3. 当二阶导数小于0的时候函数是凸，因为这时候他没有最小值，但是有最大值所以他凸。

4. 当二阶导数等于0的时候他可能是拐点，因为拐点一定是二阶导数等于0的点。

在图中，我们发现了这个函数等于0的时候正好是拐点了，所以我们得出结论，拐点一定是二阶导数等于0的点，但是我们同时要注意，拐点一定是二阶导数的0点，但二阶导数等于0的点不一定是拐点：

如果我们想要判断拐点应该怎么做呢，举个栗子：

在这个栗子中，我们先求他的二阶导，然后转换成多项式，我们发现二阶导等于0的只有x = 2，代入我们来判断他的区间，首先我们把这个二阶导以x=2为0点分为两个区间，当 $f{}''(x)> 0$ 的时候他有最小值所以是凹的，当 $f{}''(x)< 0$ 的时候他有最大值所以是凸的，结合这两个区间我们发现两边的区间凹凸性不同所以，x=2这个点是他的拐点：

1. 判断拐点首先要求二阶导

2. 然后判断二阶导等于0时，两边函数线的凹凸性

3. 如果两边的凹凸性相同那么他就不是拐点，如果凹凸性不行就是拐点

（在BB一遍：满足条件时二阶导大于0他就是凹的，小于0是凸的）

在这里结果给出了一个图表，第二行是二阶导的结果，第三行是通过二阶导对函数得出的结论。

导数的应用2（求函数的极值和最值）：

1. 极值就是函数中一个区间内的最大值或最小值

2. 最值就是整个函数中的最大值和最小值

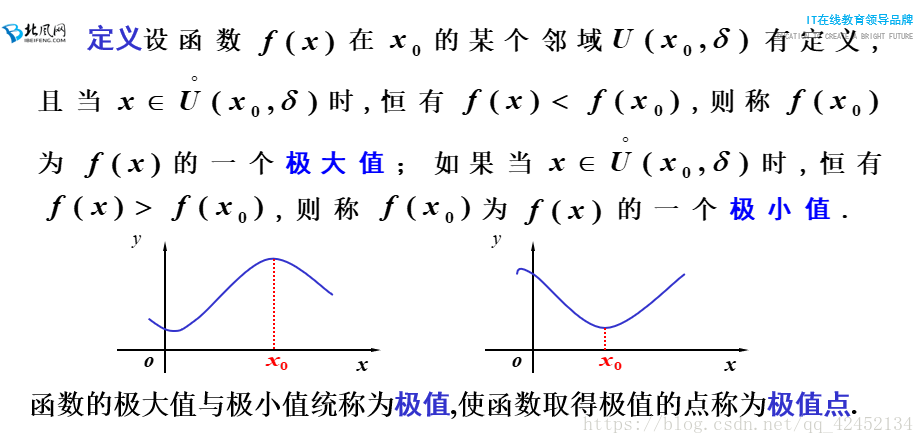
在这个图中介绍了极值的概念，我们来分析一下极值的定义：

1. 极值是在不分区间内的最大点或者最小点

2. 图中所说函数 $f(x)$ 在 $x_{0}$ 的邻域 $U(x_{0},\delta )$ 内有定义，并且 $x\in \dot{u}(x_{0},\delta )$ 时，这个是前提条件

3. 那么如果 $f(x)< f(x_{0})$ ，这时候说明 $x_{0}$ 这个点在这个区间内是最大值，因为在这个区间任意一个 $f(x)$ 都小于 $f(x_{0})$ ，这时候直接就可以称： $f(x_{0})$ 为 $f(x)$ 的一个“极大值”

4. 如果 $f(x)> f(x_{0})$ ，这时候说明 $x_{0}$ 这个点在这个区间内是最大值，因为在这个区间任意一个 $f(x)$ 都大于 $f(x_{0})$ ，这时候直接就可以称： $f(x_{0})$ 为 $f(x)$ 的一个“极小值”

（好像说些废话）

图中有个符号在回顾一下 $U(x_{0},\delta )$ ：

这个函数描述的是 U 把它想象成一个集合，后面的括号，括号中第一个元素x0，把它想象成一个中点，后面的 $\delta$ 把他想象成半径，那么就是U区间内x0为中点， $\delta$ 为左右两边的长度这么一个邻域区间。如果U上面有个句号，那么就是去中心区间，这个区间内不包含中心点x0

驻点：

接下来在引入一个概念，驻点，他就是对于可导函数的极值点就是驻点，驻点=0

极值存在的充分条件：

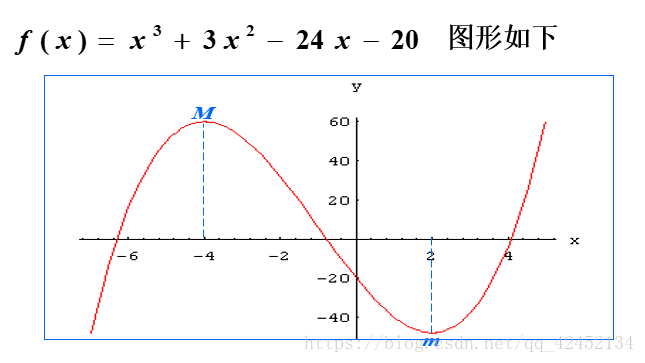
总结1：

一次BB了这么多正常情况肯定已经蒙圈了，小弟来做个总结：

1. 一阶导数可以判断函数的单调性：

①：如果函数 $y=f(x)$ 在区间内可导，那么如果他的导数在这个区间内大于0 ，则 $y=f(x)$ 在这个区间内单调递增

②：如果函数 $y=f(x)$ 在区间内可导，那么如果他的导数在这个区间内小于0 ，则 $y=f(x)$ 在这个区间内单调递减

2. 二阶导数可以判断函数的凹凸性及拐点：

①：如果函数 $y=f(x)$ 在区间内有二阶导数，那么当 ${f}''(x)>0$ 时， $f(x)$ 在这个区间内图形是凹的

②：如果函数 $y=f(x)$ 在区间内有二阶导数，那么当 ${f}''(x)< 0$ 时， $f(x)$ 在这个区间内图形是凸的

③：拐点的定义：(1) 拐点一定会二阶导数等于0的点

(2) 二阶导数不存在的也可能是拐点

3. 极值：在函数 $y=f(x)$ 上 $x_{0}$ 点的某个邻域有定义，如果这个点使函数 $y=f(x)$ 在该区间是最大值或者最小值就叫极大值或极小值（极值是指函数上一个区间内的最大值和最小值，最值是整个函数范围的，他们两个范围不同）

4. 最值：在函数 $y=f(x)$ 上如果 $x_{0}$ 使该函数处于最大值或最小值就是最值（最值是整个函数范围的，他们两个范围不同）

5. 驻点：如果 $y=f(x)$ 在极值点 $x_{0}$ 处可导，这时候导数如果等于 0 就是驻点了。

本章介绍完了，以后如果有了新的体会小弟再来更新

人工智能新手入门——高数篇（导数的应用）

导数的应用和曲线的凹凸性：