神经网络之卷积理解

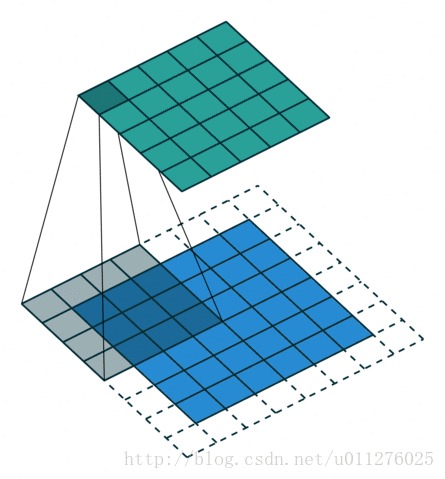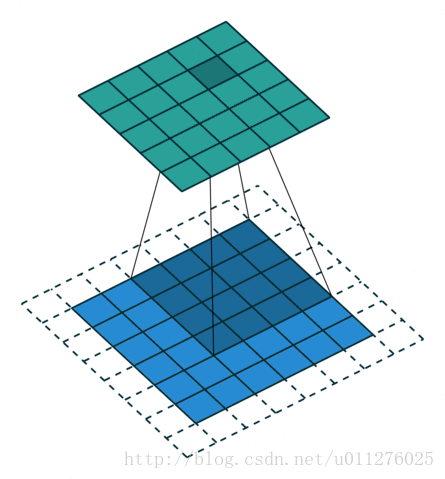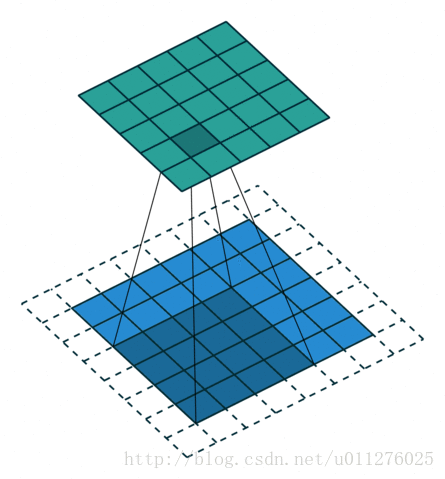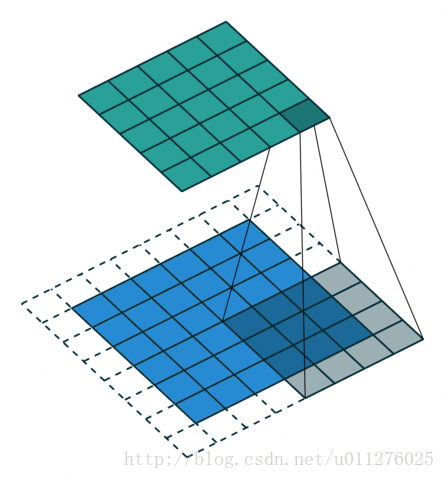
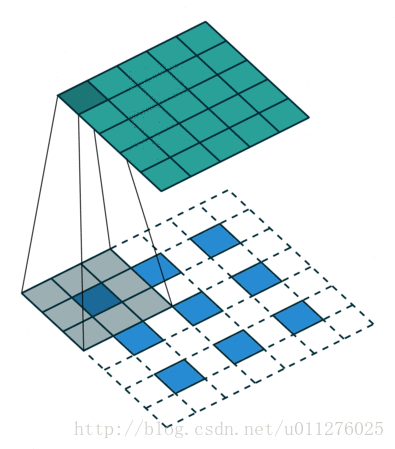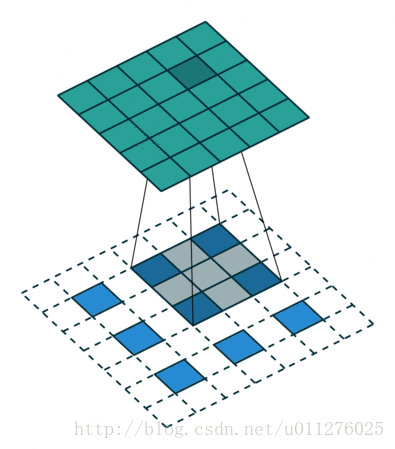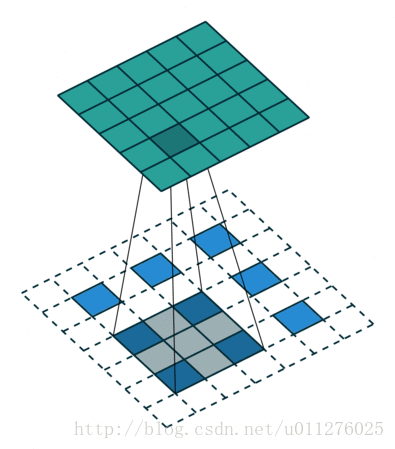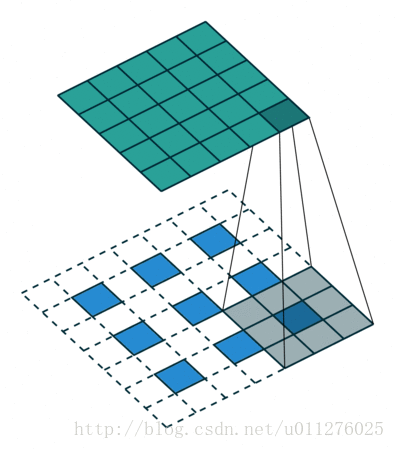
卷积看了也使用了不少时间了，最近在知乎上如何理解深度学习中的deconvolution networks看到一个关于卷积的，感觉不错，因此有把那篇讲卷积的文章A guide to convolution arithmetic for deep learning看了一遍。

首先是卷积和反卷积的输入和输出形状（shape）大小，受到padding、strides和核的大小的影响。其计算如下：

操作	卷积	反卷积
non padding，no strides	o = (i - k) + 1	o’ = i’ + (k - 1)
arbitrary padding， no strdies	o = (i - k) + 2p + 1	o’ = i’ + (k - 1) - 2p
half padding, no strides	o = i	o’ = i’
full padding, no strides	o = i + (k - 1)	o’ = i’ - (k - 1)
non padding, non-unit strides	o = $\lfloor\frac{i - k}{s}\rfloor + 1$	o’ = s(i’ - 1) + k
arbitrary padidng, non-unit strides	o = $\lfloor\frac{i + 2p- k}{s}\rfloor + 1$	$o' = s(i' - 1) + k - 2p \quad 能被strides整除\\ o' = s(i' - 1) + a + k - 2p \quad 不能被strides整除$

注1：其中o表示卷积操作输出结果，i表示卷积输入大小，k表示卷积核大小，p表示padding大小，s表示strides大小，o’, i’, k’, p’, s’则表示相应的反卷积操作大小. a 表示如果在卷积时移动步长（strides）不为1，且不能被strides整除，则其反卷积操作需要在输入i’的上边和右边补0，其大小为a，a = （i + 2k - p）.
注2：求网络感受野时，根据输出feature的一个pix反推（类似反卷积计算）原图大小，不用考虑padding的影响。

卷积操作

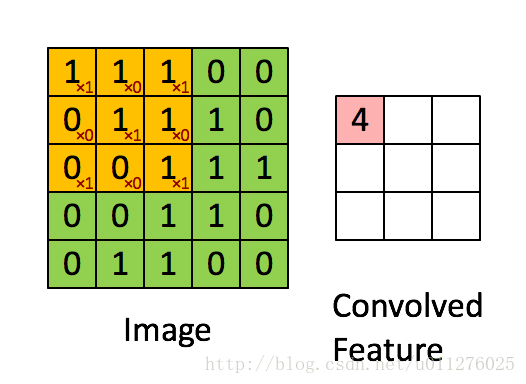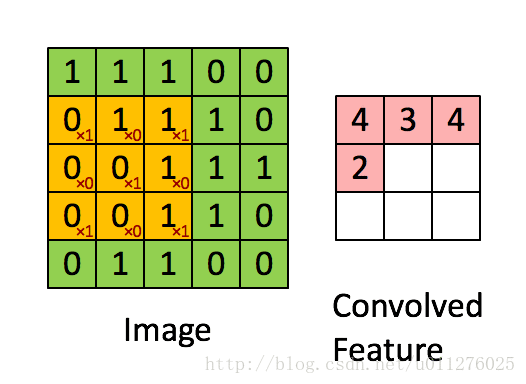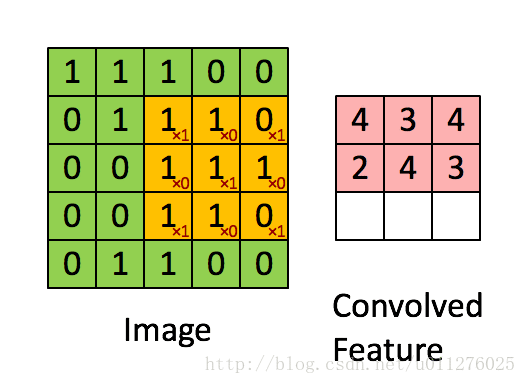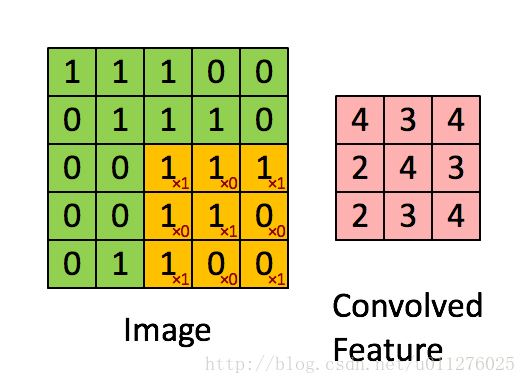
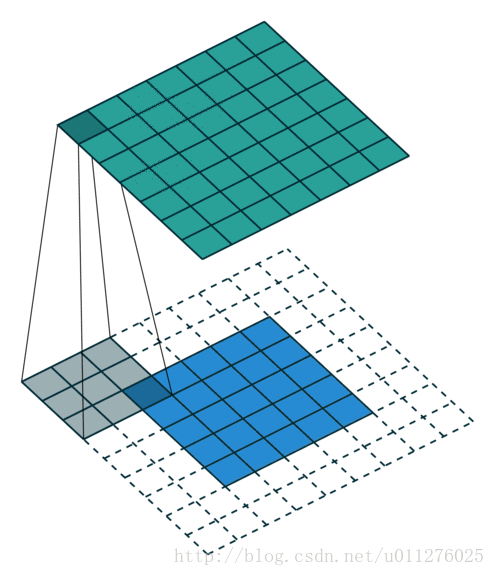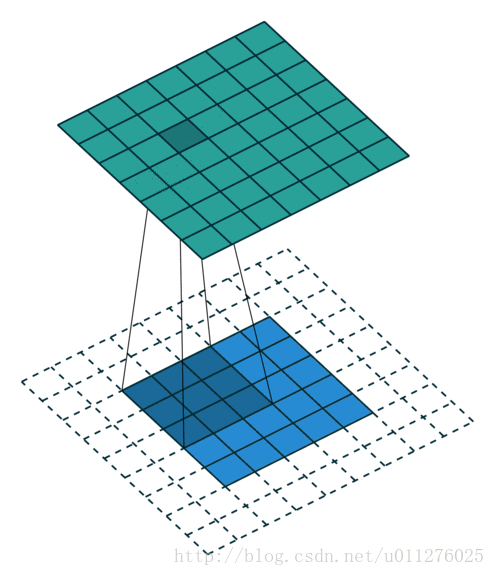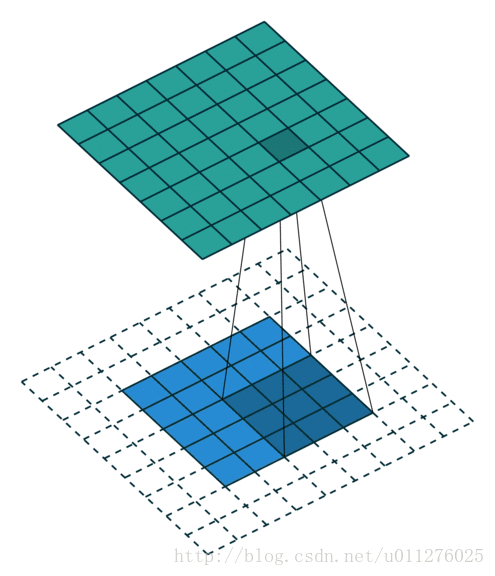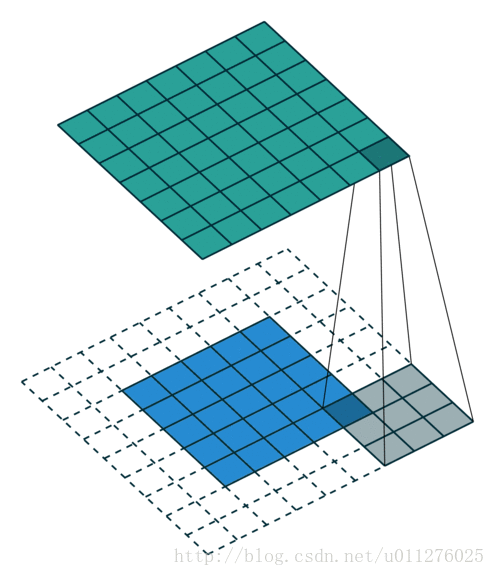
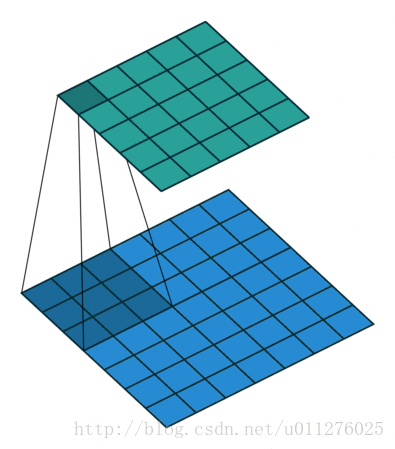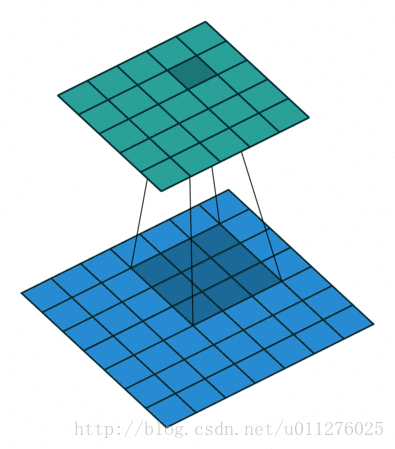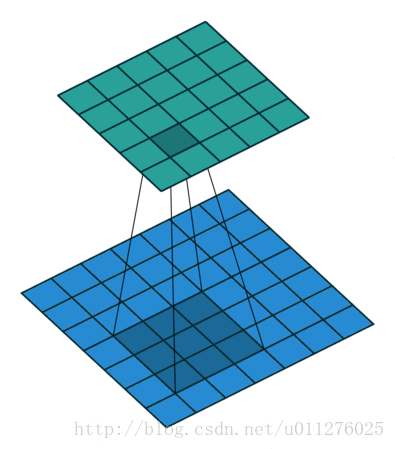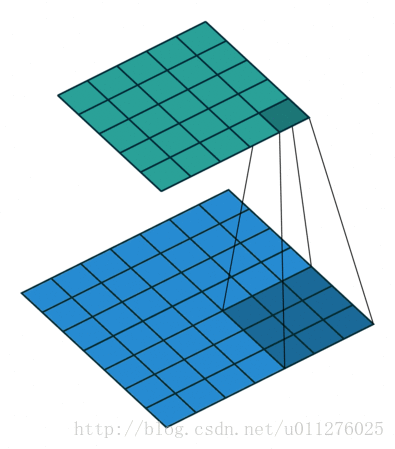
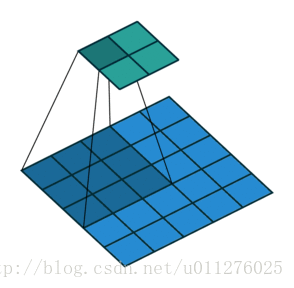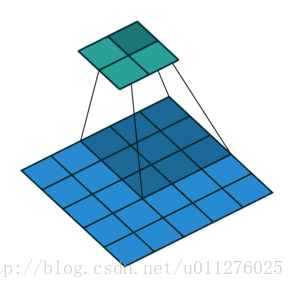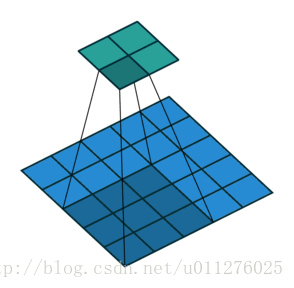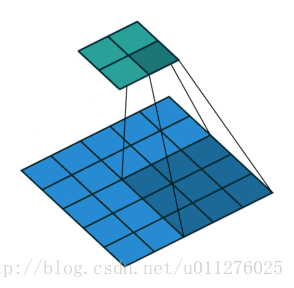
关于在数学上的卷积公式就不多说了，全是一堆公式，在图像中卷积的应用而且有点不一样，直接上一个ufldl的神图，初始接触卷积就是看的这个教程。

就是通过一个卷积核在图片像素中移动进行计算，同时，这种平移计算卷积的操作也可以看成矩阵操作，对于上面一个输入为5x5的输入，核为3x3的卷积来说（无padding且1 strides），把输入、卷积核和输出都展开为向量形式：

输入为25维的列向量 $x$
$x = [1 \quad 1 \quad 1 \quad 0 \quad 0 \quad ... \quad 0 \quad 1 \quad 1 \quad 0 \quad 0]$
核扩充为9x25维的矩阵 $C$
$C = [\begin{matrix} w_{0, 0} & w_{0, 1} & w_{0, 2} & w_{0, 3} & 0 & 0 & . . . \\ 0 & w_{0, 0} & w_{0, 1} & w_{0, 2} & w_{0, 3} & 0 & . . . \\ . . . \\ 0 & 0 & 0 & 0 & 0 & 0 & . . . \end{matrix}] = [\begin{matrix} 1 & 0 & 1 & 0 & 0 & 0 & . . . \\ . . . \\ 0 & 0 & 0 & 0 & 0 & 0 & . . . \end{matrix}]$ $C = \left[ \begin{array}{} w_{0,0}&w_{0,1}&w_{0,2}&w_{0,3}&0&0&...\\ 0&w_{0,0}&w_{0,1}&w_{0,2}&w_{0,3}&0&...\\ ...\\ 0&0&0&0&0&0&... \end{array} \right] = \left[ \begin{array}{} 1&0&1&0&0&0&...\\ ...\\ 0&0&0&0&0&0&... \end{array} \right]$
输出为4维的行向量 $y = Cx$
$x = [4 \quad 3 \quad 4 \quad 2 \quad 4 \quad 3 \quad 2 \quad 3 \quad 4]$

前向传播

通过上述的矩阵表示，则前向传播可以表示为：

y = C x

$y = Cx$

反向传播

神经网络的反向传播是通过链式求导计算的，后一层的误差乘以导数得到前一层的误差。则每层的梯度为： $\frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x}$
则对于单个 $x_j$ 有：

\frac{\partial L}{\partial x_{j}} = \sum_{i} \frac{\partial L}{\partial y_{i}} \cdot \frac{\partial y_{i}}{\partial x_{j}} = \sum_{i} \frac{\partial L}{\partial y_{i}} \cdot C_{i, j} = \frac{\partial L}{\partial y} \cdot C_{*, j} = C_{*, j}^{T} \cdot \frac{\partial L}{\partial y}

$\frac{\partial L}{\partial x_j} = \sum_i \frac{\partial L}{\partial y_i} \cdot \frac{\partial y_i}{\partial x_j} = \sum_i \frac{\partial L}{\partial y_i} \cdot C_{i,j} = \frac{\partial L}{\partial y} \cdot C_{*,j} = C_{*,j}^T \cdot \frac{\partial L}{\partial y}$
则对于

x

$x$ 有：

\frac{\partial L}{\partial x} = [\begin{matrix} \frac{\partial L}{\partial x_{1}} \\ \frac{\partial L}{\partial x_{2}} \\ . . . \\ \frac{\partial L}{\partial x_{n}} \end{matrix}] = [\begin{matrix} C_{*, 1}^{T} \cdot \frac{\partial L}{\partial y} \\ C_{*, 2}^{T} \cdot \frac{\partial L}{\partial y} \\ . . . \\ C_{*, n}^{T} \cdot \frac{\partial L}{\partial y} \end{matrix}] = C^{T} \cdot \frac{\partial L}{\partial y}

$\frac{\partial L}{\partial x} = \left[ \begin{array}{c} \frac{\partial L}{\partial x_1}\\ \frac{\partial L}{\partial x_2}\\ ...\\ \frac{\partial L}{\partial x_n} \end{array} \right] = \ \left[ \begin{array}{c} C_{*,1}^T \cdot \frac{\partial L}{\partial y}\\ C_{*,2}^T \cdot \frac{\partial L}{\partial y}\\ ...\\ C_{*,n}^T \cdot \frac{\partial L}{\partial y} \end{array} \right] = C^T \cdot \frac{\partial L}{\partial y}$

反卷积操作（transposed convolution）

反卷积，其实就是卷积转置（transposed convolution），也称为微步卷积（fractionally strided convolutions），因为在反卷积中可能出现移动小于一步的情况，下面会介绍。

根据上面矩阵表示卷积的前向和反向传播的过程，其反卷积的操作就非常简单了，只需要对C进行转置就好了， $C' = C^T$ .
即：

x = C^{T} y

$x = C^Ty$

\frac{\partial L}{\partial x} = C \cdot \frac{\partial L}{\partial y}

$\frac{\partial L}{\partial x} = C \cdot \frac{\partial L}{\partial y}$
因此，在反卷积中不需要改变核的大小。

不使用padding和strides

卷积操作

这种类型是最简单的

输出大小为： $o = (i - k) + 1$

解释： 只看一次重做到右的滑动，一共滑动 $i - k$ 次，在加上本身初始所在的位置，所以输出为 $(i - k) + 1$ 。

反卷积操作

为了使得到的输出结果比输出结果的shape大，需要改变其padidng的值。

k’ = k
s’ = s
p’ = k-1

解释： $k$ 和 $s$ 在反卷积中不改变，卷积操作使得输出减小了 $k - 1$ , 则反卷积操作需要使输出还原到原大小，即输出增加 $k-1$ , 得： $i' + (k - 1) = (i ' + 2p' - k') + 1$ –> $p' = k - 1$ .

其过程如下所示：

输出大小为： $o' = i' + (k - 1)$

解释： $o' = （i' + 2p' - k') + 1 = i' + (k - 1)$

使用padding和不使用strides

卷积操作

使用padding在输入图像周围填充0，使输出的结果shape大于输入的结果（不是反卷积）。在实际实现卷积操作中没有计算这些0的乘法

输出大小为： $o = (i - k) + 2p + 1$

**解释：**padding在矩阵周围增加了p个单位的0，因此其输入大小增加为 $i + 2p$ , 即， $o = (i + 2p -k) + 1$

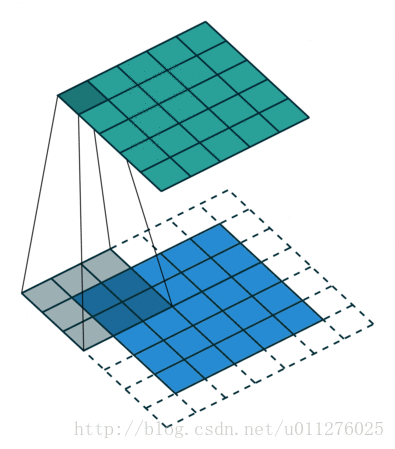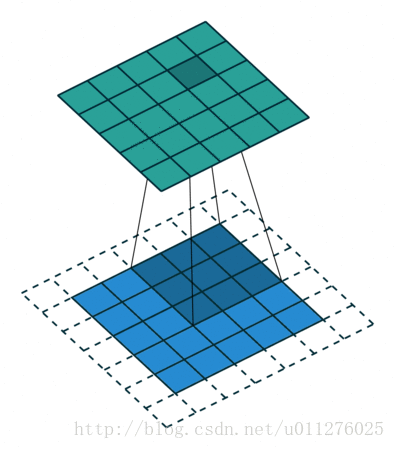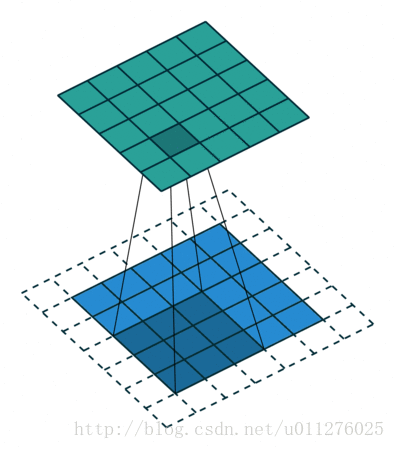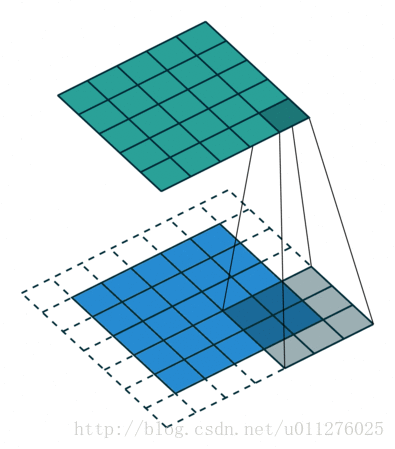
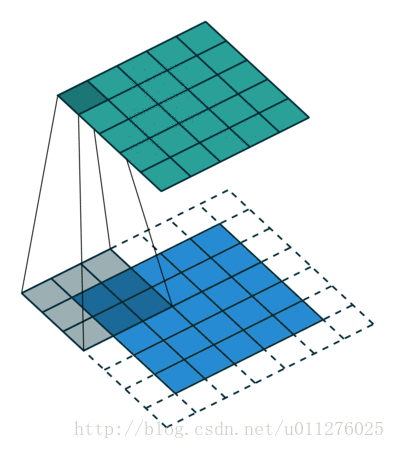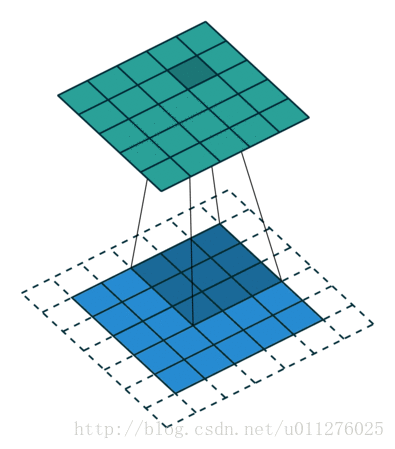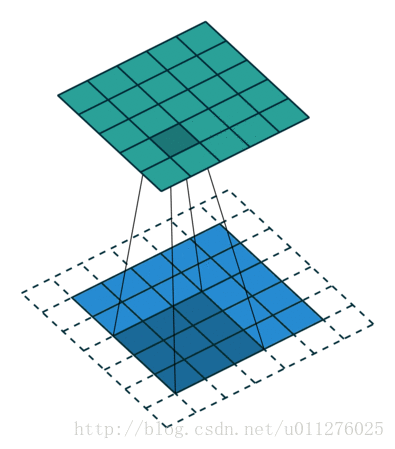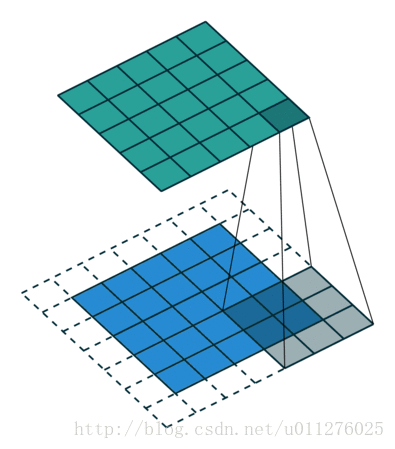
反卷积操作

由于在卷积时在输入的四周补0了，所以在反卷积时需要重新计算 $p'$ , $p' = k - p - 1$ .

解释：同理，卷积操作减少了 $k - 2p - 1$ , 在反卷积中需要增加回来，则， $i' + (k - 2p -1) = (i' + 2p; - k') + 1$ –> $p = k - p - 1$ .

输出大小为： $o' = i' + (k - 1) - 2p$

解释： $o' = （i' + 2p' - k') + 1 = i' + 2(k - p - 1) - k + 1 = i' + k - 1 - 2p$

注意： $p'$ 的重新计算和 $o'$ 中使用的是 $p$

奇数核一半的padding和不使用strides

这种结构比较好玩，就是使输入和输出的大小相同，VGG就是使用这种结构。

卷积操作

核： $k=2n+1,$ ，stride： $s = 1$ ，padding： $p = \lfloor k/2 \rfloor = n$

输出大小为： $o = i + 2\lfloor k/2 \rfloor - (k - 1) = i + 2n - 2n = i$

反卷积操作

由于卷积的输入和输出的形状相同，则反卷积操作与卷积操作也相同。
即, $k' = k, p' = p, s' = s$

输出大小为： $o' = i' + (k - 1) - 2p = i' + 2n - 2n = i'$

奇数核-1大小的padding和不使用strides

stride： $s = 1$ ，padding： $p = k - 1$ 。

卷积操作

输出的结果比输入的大，输出增加了p大小。

输出大小为： $o = i + 2(k - 1) - (k - 1) = i + (k - 1)$

反卷积操作

相当于没有使用padding的反卷积操作，就是卷积操作中输出增加了 $k - 1$ ，则在反卷积中不使用padding，则输出大小减少 $k - 1$ 。

输出大小为： $o' = i' + (k - 1) - 2p = i' - (k - 1)$
注意：使用的是 $p$ 。

不使用padding和使用strides

即，卷积核一次移动多步。

卷积操作

输出大小为： $o = \lfloor \frac{i - k}{s} \rfloor + 1$
注意：上式进行了向下取整，也就是遇到奇数无法除尽的时候需要向下取整。这种情况需要额外注意，因为在反卷积中需要在其上面和左边补0, 该图在下一节一起放出。

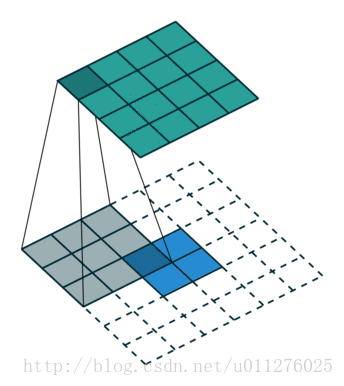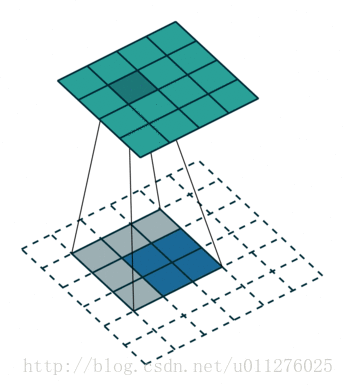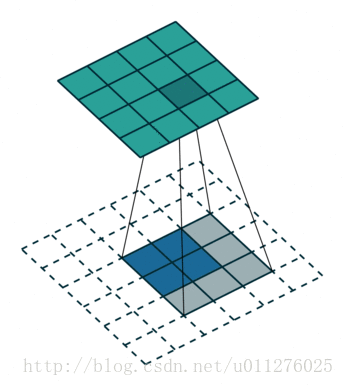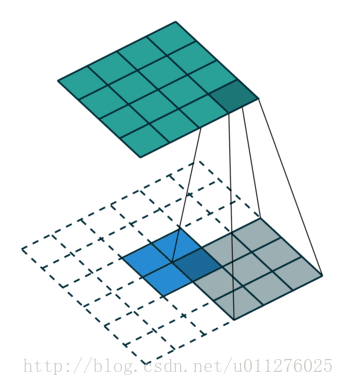
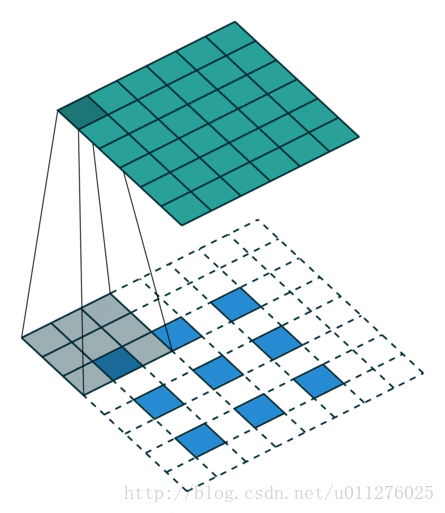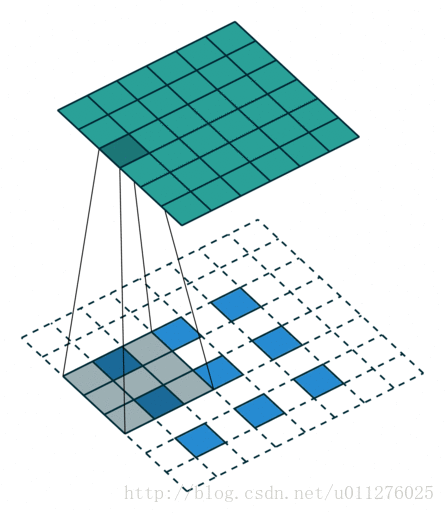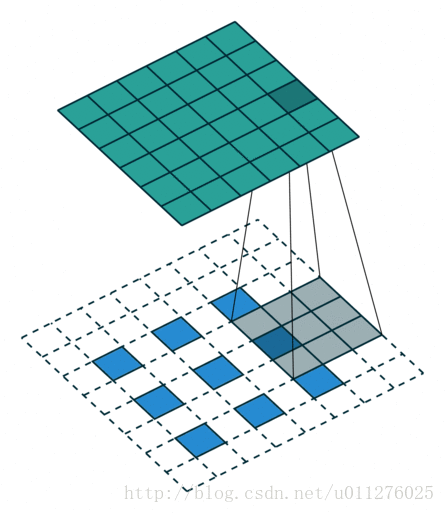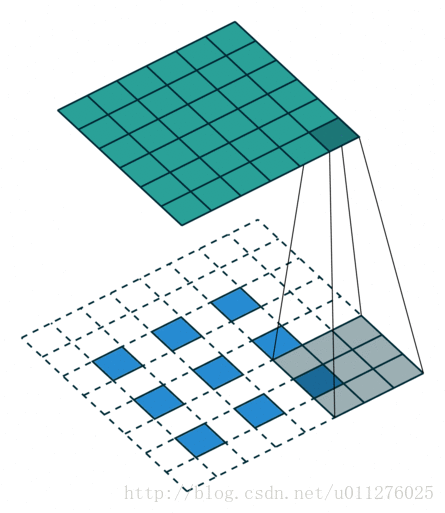
反卷积操作

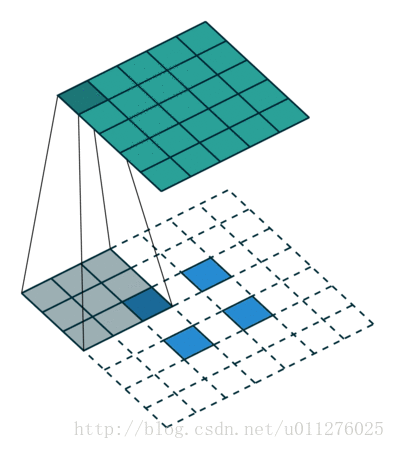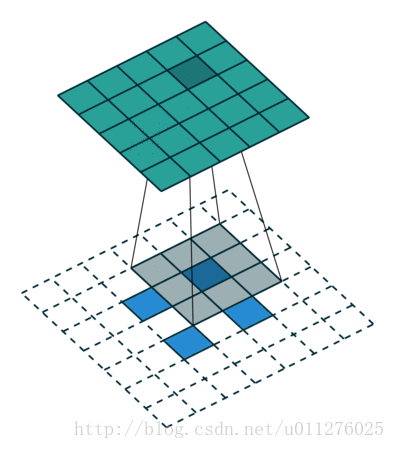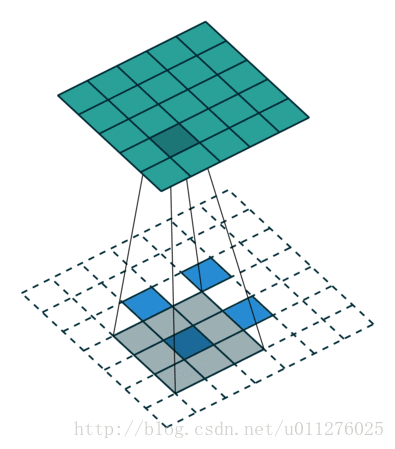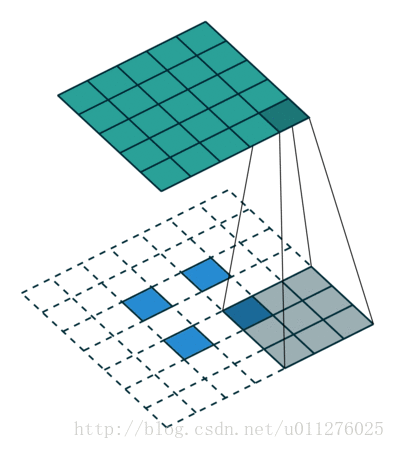
这种情况的反卷积比较好玩，需要在输入数据中插0。这也是微步卷积的由来（fractionally strided convolutions），由于在输入中插入0，导致strides移动<1。

核： $k' = k$ ，stride： $s' = 1$ ，padding： $p' = k - 1$
注意 $i'$ 的大小为在输入中插入了s - 1个0。

输出大小为： $o' = s(i' - 1) + k$

使用padding和使用strides

卷积操作

和不使用padding差不多，只不过四周补0了.

输出大小为： $o = \lfloor \frac{i + 2p - k}{s}$ + 1

反卷积操作

对于移动步数刚好整除的
核： $k' = k$ ，stride： $s' = 1$ ，padding： $p' = k - p - 1$

输出大小为： $o' = s(i' - 1) + k - 2p$

对于无法整除的
这种情况需要在输入矩阵的上边和右边增加a排0，其中 $a = (i + 2p - k)$

输出大小为： $o' = s(i' - 1) + k + a - 2p$

references

图片来自：https://github.com/vdumoulin/conv_arithmetic
文章参考：A guide to convolution arithmetic for deep learning