二分搜索基础知识
一、二分搜索常见的应用场景
1、在有序序列中查找一个数
arr: ... .... ...mid ... ... ... n
2、并不是非要在有序序列中才能得到应用
二、二分搜索常见的考察点
1、对于边界条件的考察以及代码实现的能力。
三、二分搜索常见题目的变化
1、给定处理或查找的对象不同
2、判断条件不同、
3、要求返回的内容不同
4、在有序循环数组中进行二分搜索。1,2,3,4,5循环之后可以是:1,2,3,4,5或2,3,4,5,1或3,4,5,1,2或4,5,1,2,3或5,1,2,3,4
四、二分搜索的注意事项
mid = (left +right)/2 当数组下标较大的时候容易产生溢出。
更安全的写法:mid = left + (right - left)/2
五、二分搜索的代码实现
def binary_search(list,key):
left,right = 0,len(list)
while left < right:
mid = left + (right-left)/2
if list[mid] == key:
return mid
elif list[mid] > key:
right = mid-1
else:
left = mid+1
return -1
二分搜索经典案例
案例一:
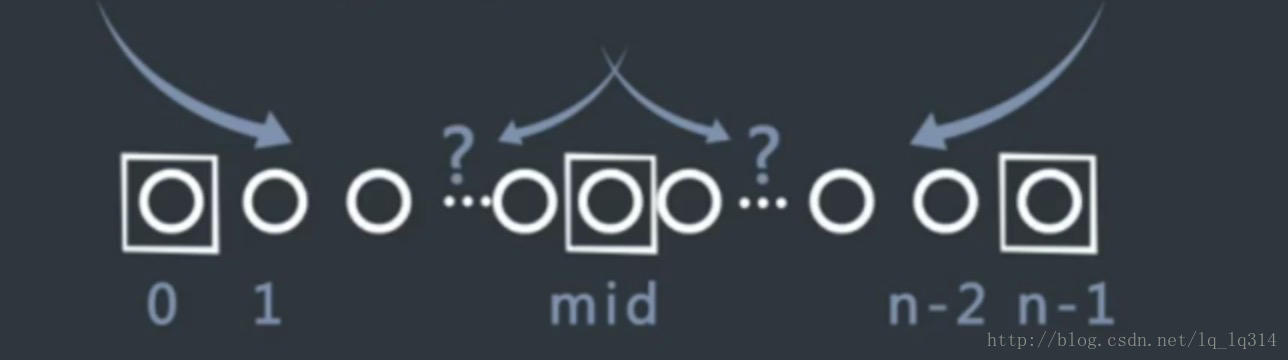
给定一个无序数组arr,已知任意相邻的两个元素,值都不重复。请返回任意一个局部最小的位置。
所谓局部最小的位置是指,如果arr[0]<arr[1],那么位置0就是一个局部最小的位置。如果arr[N-1](也就是arr最右的数)小于arr[N-2],那么位置N-1也是局部最小的位置。如果位置 i 既不是最左位置也不是最右位置。那么只要满足arr[i]同时小于它左右两侧的值即(arr[i-1]和arr[i+1]),那么位置i也是一个局部最小的位置。
思路:
本题依然可以用二分搜索来实现,时间复杂度为O(logN)
1、arr为空或长度为0,返回-1,表示局部最小位置不存在。
2、如果arr长度为1,返回0,因为此时0是局部最小位置。
3、如果arr长度大于1。首先检查两头的位置,考察arr[0]<arr[1] 如果是,直接返回arr[0] ,同样如果arr[n-1]<arr[n-2],直接返回arr[n-1],如果两头的位置都不是局部最小,那么考察中间位置mid的情况,如果mid的值既小于左边第一个值,又小于右边第一个值。那么此时mid就是局部最小的值,返回即可。如果mid比左边的小,而比右边的大,那么在mid的左边一定存在局部最小的情况,此时可以直接对左部分进行同样逻辑的二分搜索。反之在mid的右边一定存在局部最小的情况,对右部分继续进行同样逻辑的二分搜索。如果mid位置的数比左右都大,说明左右两边都存在局部最小的情况。
案例二:
给定一个有序数组arr,在给定一个整数num,请在arr中找到num这个数出现的最左边的位置。
思路:
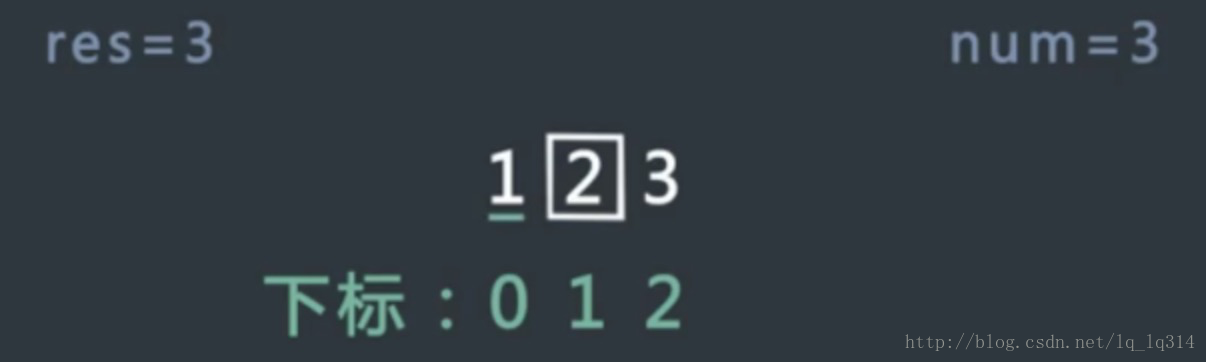
这里我们以数组[1,2,3,3,3,3,4,4,4,4,4,4]为例,num = 3
1、先生成一个全局变量res,用来记录最后一次找到3的位置。初始时res = -1.
2、首先找到中间的数,如果>3,则在左部分进行二分搜索,此时找到了3,将res的值更新为3,
3、找到3之后,继续对左部分进行二分搜索,接下来找到中间的数2,接着对右部分进行二分搜索,找到3,此时就是我们要的值,更新res的值,为2,返回2。
案例三:
给定一个有序数组arr,返回arr中的最小值。有序循环数组是指,有序数组左边任意长度的部分放到右边去,右边的部分拿到左边来。比如数组[1,2,3,3,4],是有序循环数组,[4,1,2,3,3]也是。
思路:
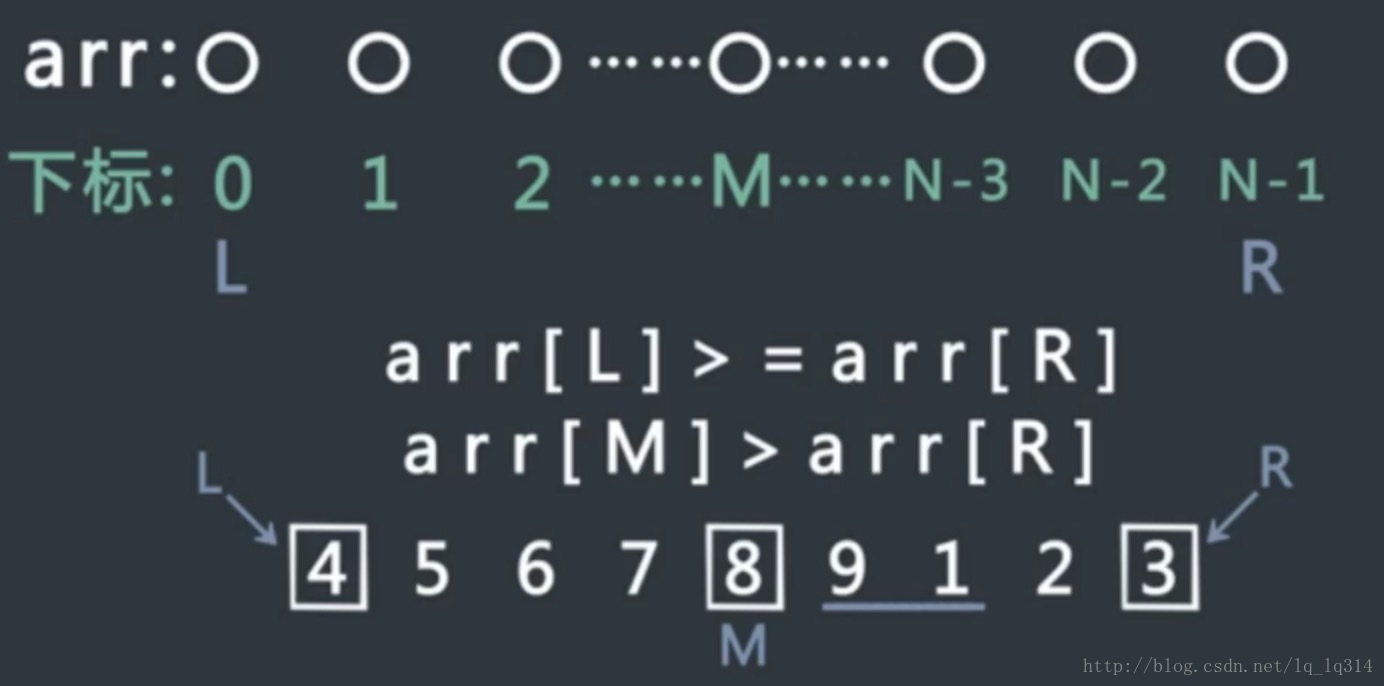
1、假设我们在数组arr的L到R之间找最小值,如果arr[L] < arr[R],说明这个数组整体有序,最小值自然是最左边的arr(L),返回arr(L)即可。
2、如果arr[L] >= arr[R],说明中间可能包含循环的部分,比如数组[2,2,3,1,2]我们考虑L到R的处于中间位置M的数,
3、如果发现arr(L)>arr(M),说明最小值只可能出现在L到M的范围上,因为只有arr[M]是循环过的部分时,才有可能出现arr[L]>arr[M]的情况。比如数组[7,8,9,1,2,3,4,5,6],arr[L] = 7 ,arr[M] = 2 , arr[R] = 6,最小值1依旧在左半部分,此时在左部分继续进行二分搜索。
4、如果发现arr[M]>arr[R],说明最小值只可能出现在右半部分,比如说数组[4,5,6,7,8,9,1,2,3],最小值1出现在右部分,此时在右部分就继续进行二分搜索。
5、如果arr[L]>arr[M]和arr[M]>arr[R]这两个条件都不满足,即arr[L]<=arr[M]和arr[M]<=arr[R],说明三值相等,我们无法继续用二分搜索实现寻找最小值,比如数组[2,2 ... ... 2,1,2 ... ... 2,2。只能通过遍历的方式在arr[L]和arr[M]上寻找最小值。
案例四:
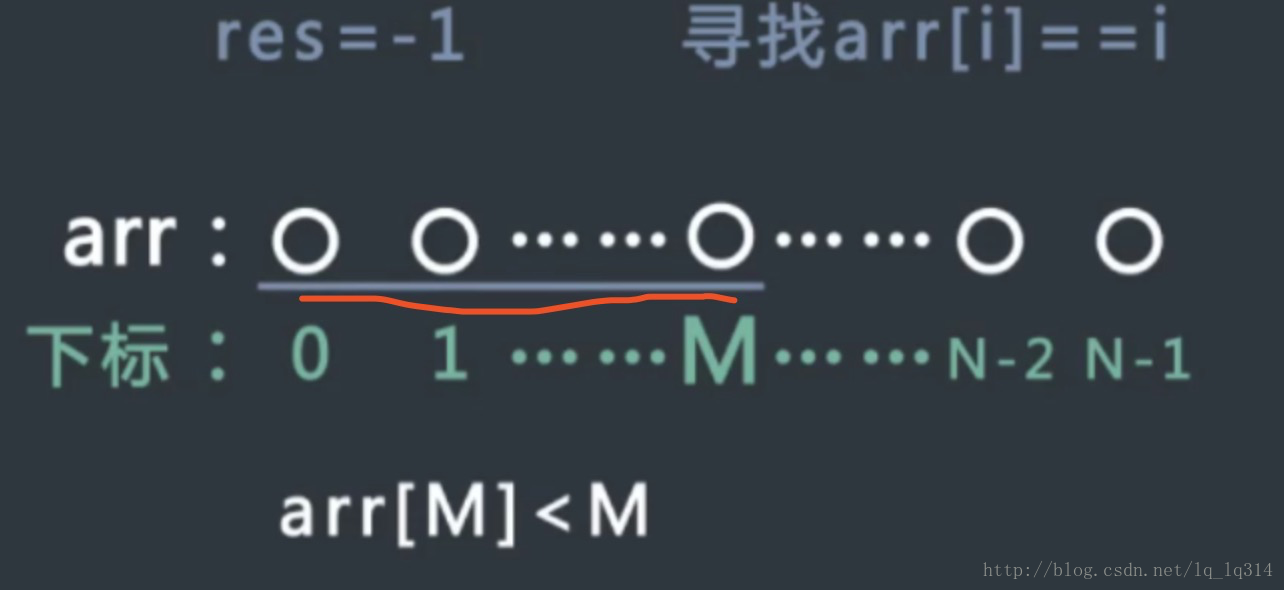
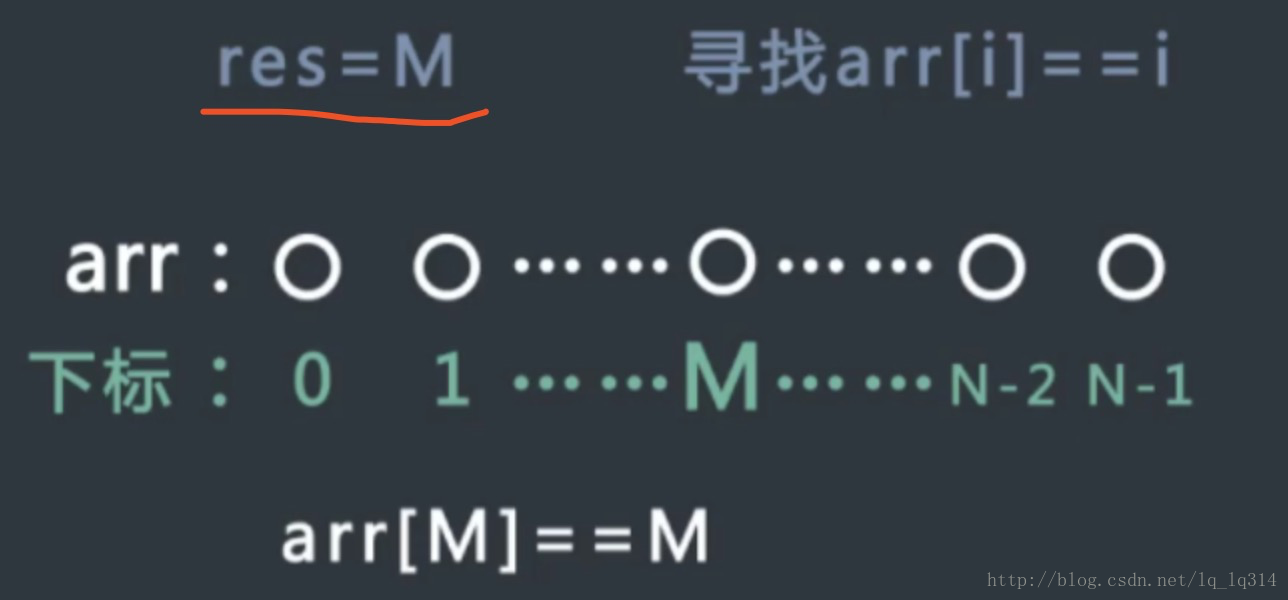
给定一个有序数组arr,其中不含有重复元素,请找到满足arr[i] == i条件的最左的位置。如果所有位置上的数都不满足条件,返回-1.
思路:
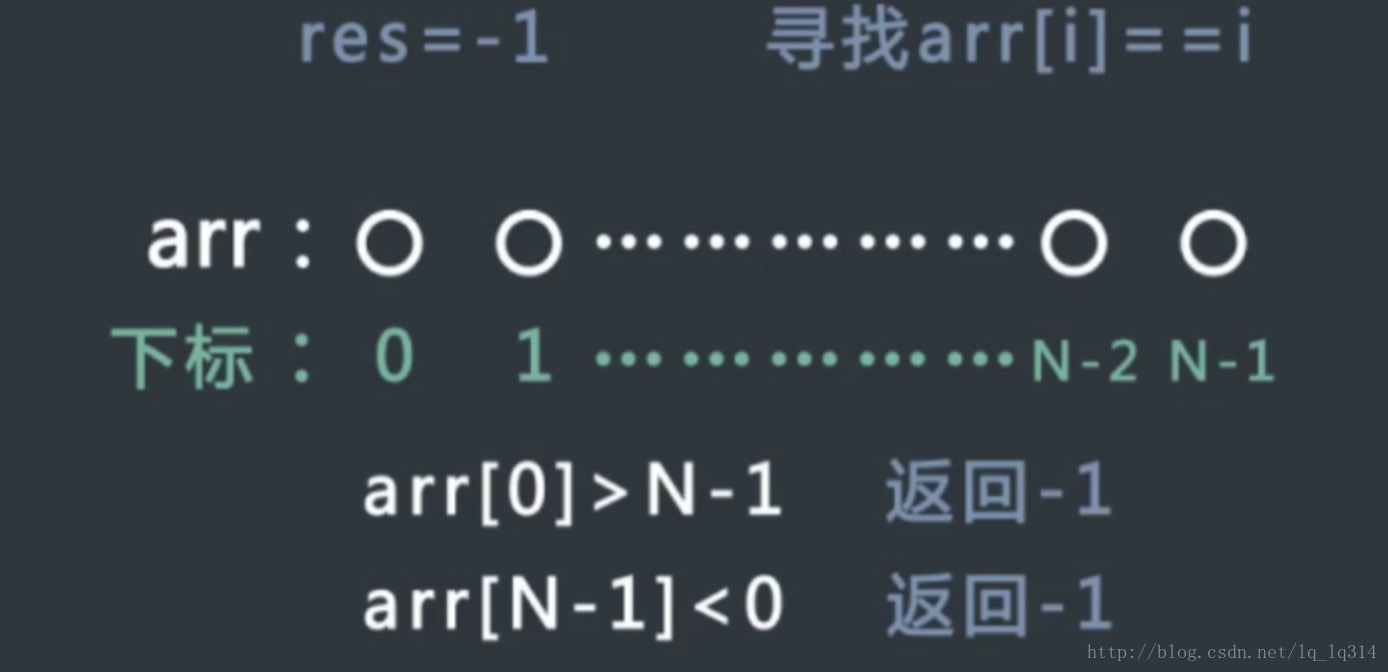
1、首先生成全局变量res,初始值为-1,如果arr的长度为N。
2、初始时现考虑arr[0]的值,如果arr[0]>N-1,因为整个数组有序,所以整个数组上的值都>N-1,不会存在arr[i] = i 的情况。直接返回-1,同理我们要考虑arr[n-1]<0的情况,如果成立,也直接返回-1。
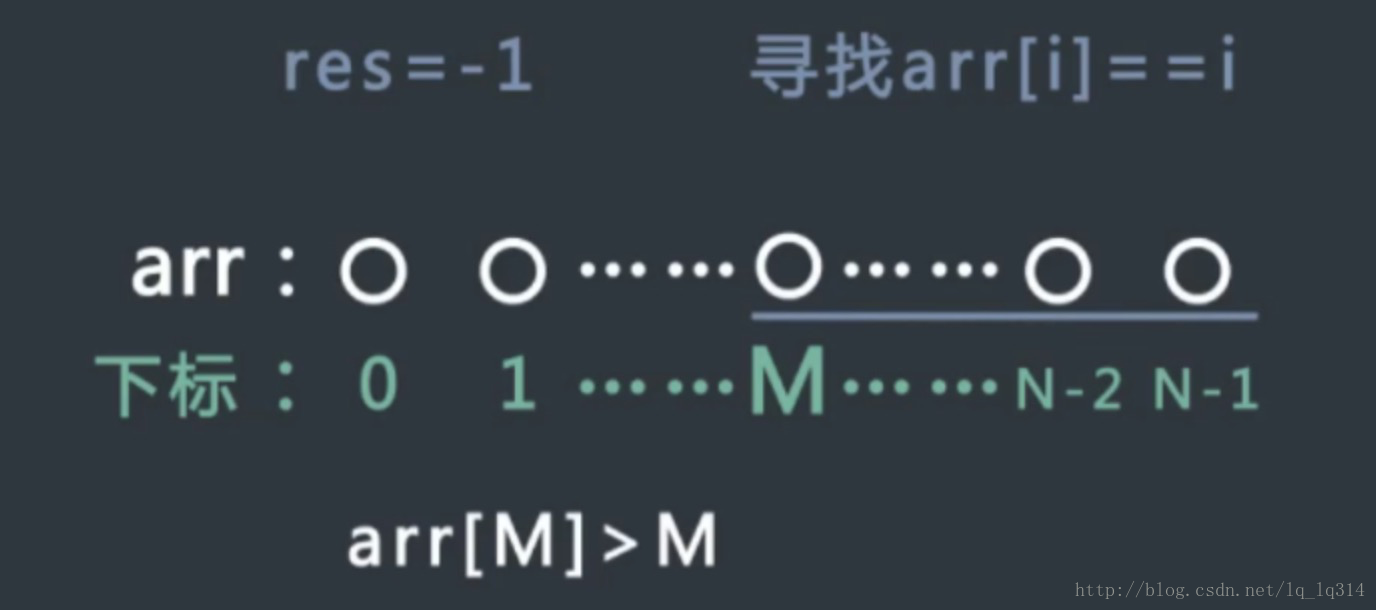
3、如果上面两种情况都没有发生,我们就考察中间位置的数M情况,如果arr[m]>m,所以m到n上都不会出现arr[i] = i 情况,我们继续对0到m-1的情况上进行二分就可以了。
4、如果arr[m]<m,因为数组即没有重复值,同时又是递增,所以从m位置到0位置上的值是从右到左是递减的,而递减量最小为1,而位置的值,从最右到最左递减量是严格的1,所以整个0到m上都不会出现arr[i] = i的情况,那么此时之用在m+1到n的情况下进行二分搜索就可以了。
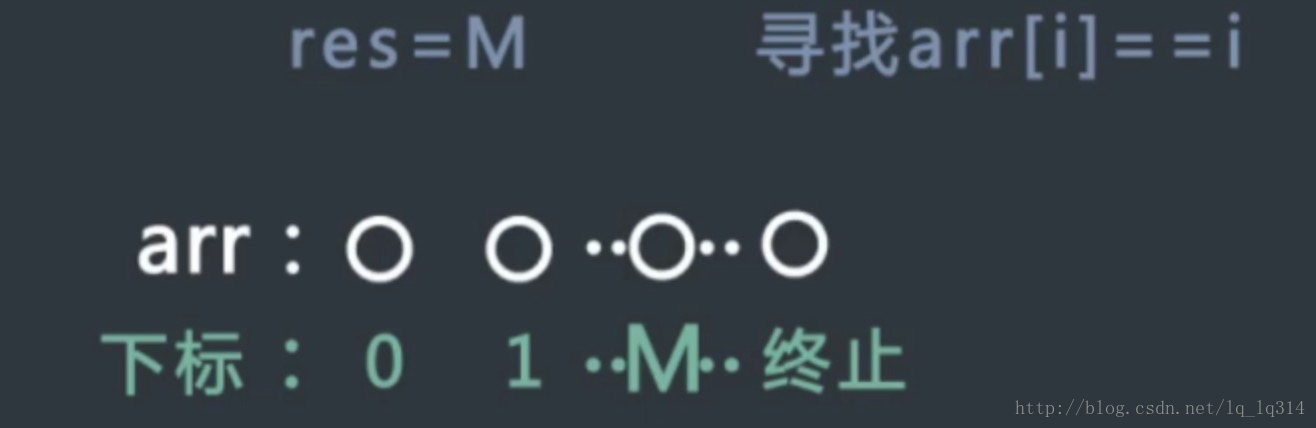
5、如果arr[m] = m,用res记录下当前的值,但同时我们要找到的是最左的位置,所以依然是0到m的范围上进行二分搜索。
案例五:
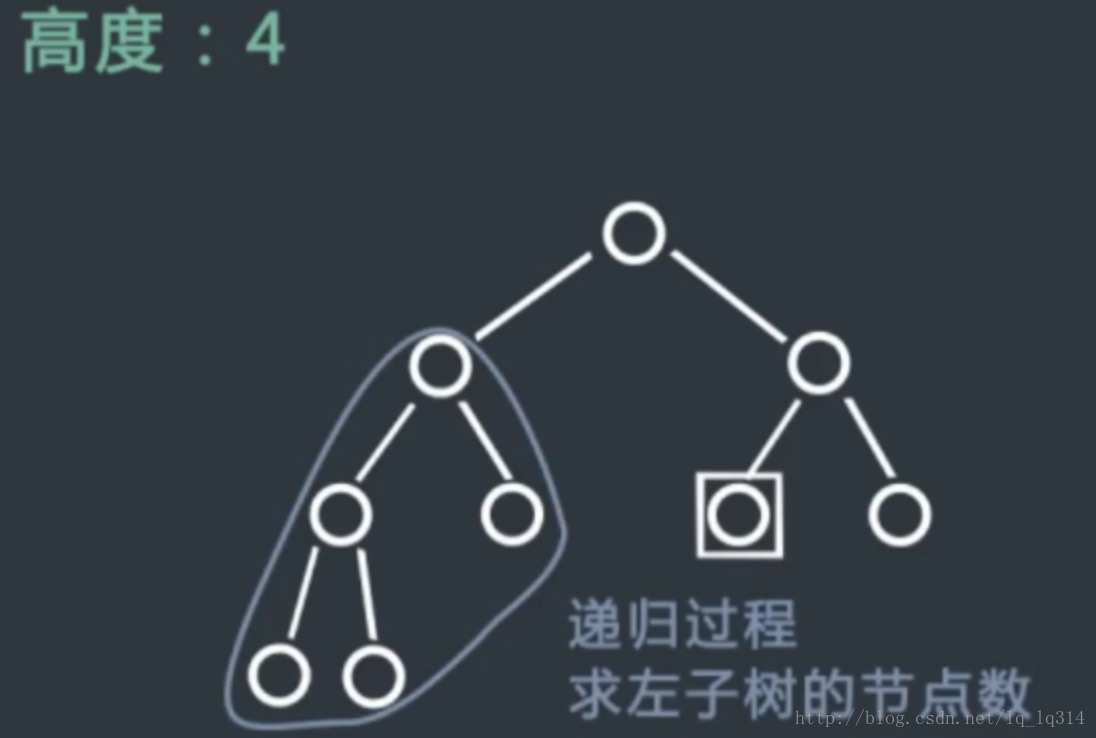
给定一棵完全二叉树的头节点head,返回这棵树的节点个数。如果完全二叉树的节点树为N,请实现时间复杂度低于O(N)的解法。
思路:
这道题看似和二分搜索没有关系,实质上最优解就是来自与二分搜索,完全二叉树节点的增加和减少和堆类似。利用它的性质,是的我们使用二分搜索统计它的个数成为了可能。
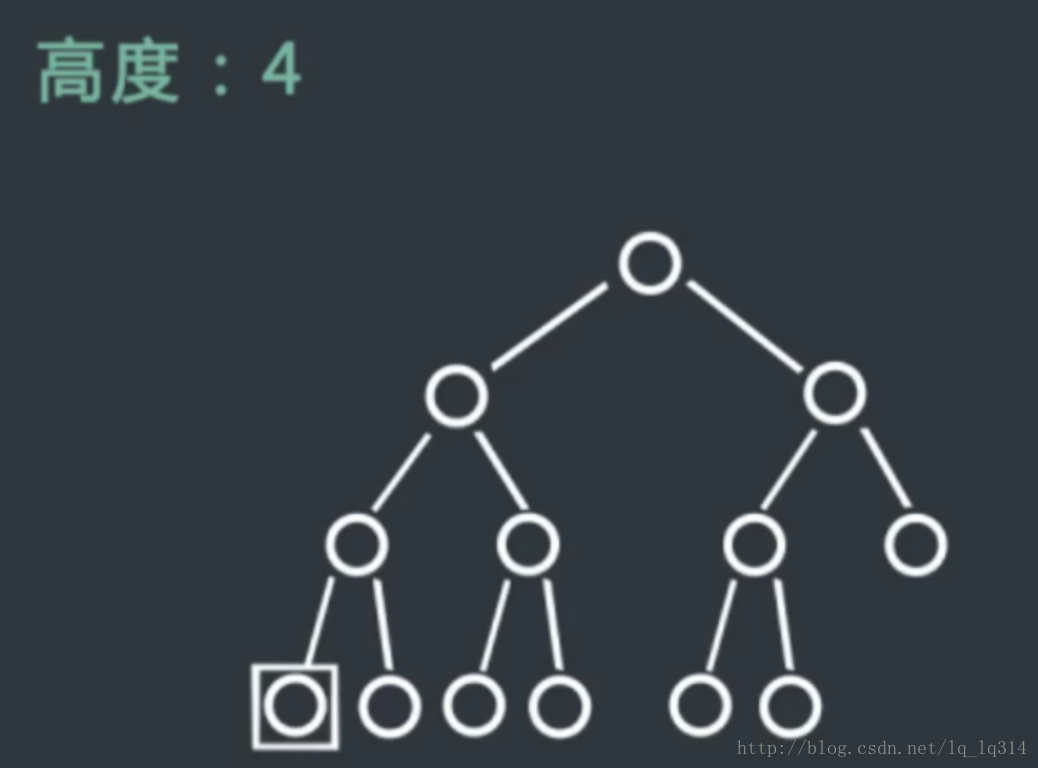
1、首先找到二叉树最左边的节点,最左边的节点一定是在二叉树的最后一层,我们可以通过它来统计二叉树的高度,得到层数为h,
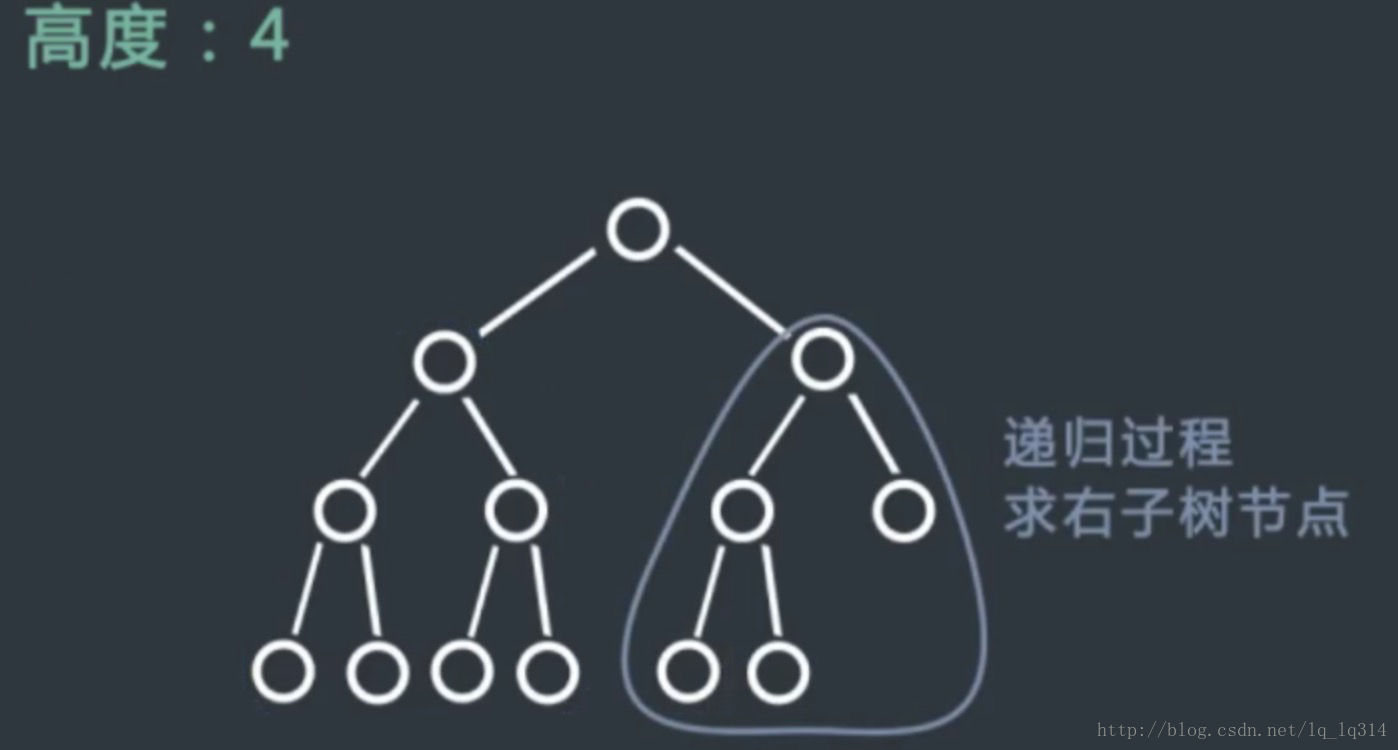
2、然后我们找到二叉树头节点的右子树的最左边的节点,如果能到达最后一层,那么说明头节点的左子树一定是一棵满二叉树,我们可以直接根据满二叉树的计算公式算出左子树的节点个数,加上头节点,剩下的节点个数我们可以通过递归的方法用相同的方式在右子树上求出节点个数。

3、如果头节点的右子树的最左节点不能到达最后一层,那此时头节点的右子树一定是比左子树少一层的满二叉树,我们可以直接根据满二叉树的计算公式算出右子树的节点个数,加上头节点,剩下的节点个数我们可以用相同的方法递归的求出左子树的界定个数。

如果使用普通遍历的方式,时间复杂度为O(N)
最优解的过程,时间复杂度为O(logH^2),H为这颗完全二叉树的高度。
案例六:
如果更快的求一个整数k的N次方。如果两个整数相乘并得到结果的时间复杂度为O(1),得到整数k的N次方的过程请实现时间复杂度为O(logN)的方法。
普通的做法是K^n = K*K........*K*K(n个K),乘了n-1次,时间复杂度为O(N)。
但其实是可以在时间复杂度为O(logN)实现的,这里我们举个例子来说。
思路:
10^75 = 10^1001011(75的二进制表达式)
= 10^64 * 10^8 * 10^2 * 10^1
= 10^1000000 * 10^1000 * 10^10 * 10^1
| 10^64 | 10^32 | 10^16 | 10^8 | 10^4 | 10^2 | 10^1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
n的二进制可以天然的把我们的乘法过程划分的十分优良,这一思想也是来自于二分搜索。