1 矩阵

1.1 矩阵的定义及运算

1.1.1 矩阵的定义

矩阵是一个数表，由 m x n 个数排成的 m 行 n 列的数表

[\begin{matrix} a_{11} & a_{12} & \dots & a_{1 n} \\ a_{21} & a_{22} & \dots & a_{2 n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m 1} & a_{m 2} & \dots & a_{m n} \end{matrix}]

$\begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\ \end{bmatrix}$
称为一个m行n列的矩阵，

a_{i j}

$a_{ij}$ 为矩阵第i行j列的元素。
m=n时矩阵为方阵；只有

a_{i i}

$a_{ii}$ 不全为0的方阵叫对角阵；

a_{i i}

$a_{ii}$ =1的对角阵为单位矩阵，记做I；元素都是0的矩阵为0矩阵。

1.1.2 线性方程组

{\begin{cases} 2 x_{1} + x_{2} - x_{3} & = 1 \\ x_{1} + x_{3} & = - 2 \end{cases}

$\begin{cases} 2x_1+x_2-x_3&=1\\ x_1+x_3&=-2\\ \end{cases}$
对应的系数矩阵为：

A = [\begin{matrix} 2 & 1 & - 1 \\ 1 & 0 & 1 \end{matrix}]

$A= \begin{bmatrix} 2&1&-1\\ 1&0&1\\ \end{bmatrix}$
对应的曾广矩阵为：

B = [\begin{matrix} 2 & 1 & - 1 & 1 \\ 1 & 0 & 1 & - 2 \end{matrix}]

$B= \begin{bmatrix} 2&1&-1&1\\ 1&0&1&-2\\ \end{bmatrix}$

1.1.3 矩阵的运算

运算	说明
同型矩阵	行列对应相等
矩阵相等	对应元素相同的同型矩阵
矩阵加法	同行矩阵才有定义，对应不元素相加
矩阵数乘	所有元素乘以对应的实数：kA = （k $a_{ij}$ ）
矩阵乘法	$A_{m \times t}B_{t \times n} = C_{m \times n} = (c_{ij})_{m \times n}$ ，其中 $c_{ij} = \sum_{k=1}^t{a_{ik}b_{kj}}$
矩阵等价	A通过初等变换得到B
矩阵相似	$A=M^{-1}BM$

1.2 矩阵的两个图

2x2矩阵

{\begin{cases} 2 x - y = 0 \\ - x + 2 y = 3 \end{cases} \to [\begin{matrix} 2 & - 1 \\ - 1 & 2 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}] = [\begin{matrix} 0 \\ 3 \end{matrix}] x [\begin{matrix} 2 \\ - 1 \end{matrix}] + y [\begin{matrix} - 1 \\ 2 \end{matrix}] = [\begin{matrix} 0 \\ 3 \end{matrix}] \to {\begin{cases} x = 1 \\ y = 2 \end{cases}

$\begin{cases}2x-y=0\\-x+2y=3\\\end{cases} \rightarrow \begin{bmatrix}2&-1\\-1&2\\\end{bmatrix} \begin{bmatrix}x\\y\\\end{bmatrix}= \begin{bmatrix}0\\3\\\end{bmatrix} \\ x \begin{bmatrix}2\\-1\\\end{bmatrix} + y \begin{bmatrix}-1\\2\\\end{bmatrix}= \begin{bmatrix}0\\3\\\end{bmatrix} \rightarrow \begin{cases}x=1\\y=2\\\end{cases}$

1.2.1 行图（row picture）

通过交点可以判断方程是否有解
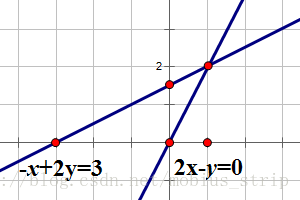
这里写图片描述

1.2.2 列图（column picture）

列向量的线性组合
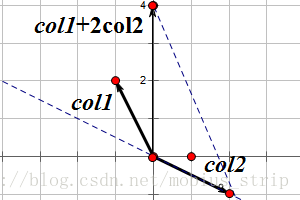
这里写图片描述

1.2.3 行列运算

[\begin{matrix} c o l 1 & c o l 2 & c o l 3 \end{matrix}] [\begin{matrix} a \\ b \\ c \end{matrix}] = a * c o l 1 + b * c o l 2 + c * c o l 3 [\begin{matrix} a & b & c \end{matrix}] [\begin{matrix} r o w 1 \\ r o w 2 \\ r o w 3 \end{matrix}] = a * r o w 21 + b * r o w 2 + c * r o w 3

$\begin{bmatrix}col1&col2&col3\\\end{bmatrix}\begin{bmatrix}a\\b\\c\\\end{bmatrix}=a*col1+b*col2+c*col3\\ \begin{bmatrix}a&b&c\\\end{bmatrix}\begin{bmatrix}row1\\row2\\row3\\\end{bmatrix}=a*row21+b*row2+c*row3$

1.3 消元法与LU分解

1.3.1 矩阵的初等变换

ID	初等行（列）变换
1	交换两行（列）的位置
2	用一非零数程昱某一行的所有元素
3	把矩阵的某一行（列）的适当倍数加到另一行（列）上去

经过初等变换后，将矩阵转化成阶梯形式，如果曾广矩阵有非零主元则方程无解；如果阶梯矩阵对应的系数部分主对角含零，则有无穷解；

初等矩阵：对单位矩阵做一次初等变换得到的矩阵；行变换等于左乘初等矩阵，列变换等价于右乘初等矩阵

1.3.2 LU分解

高斯消元法：对曾广矩阵实施行初等变换化为行（简化）阶梯形

通过消元法将矩阵A转换成矩阵B（阶梯，上三角），对应行变换左乘的初等矩阵记为： $E1_,...,E_k$ 则有：
$E_k..E_1A = B \rightarrow A = E_1^{-1}..E_k^{-1}B，记L=E_1^{-1}...E_k^{-1}，则A= LU$

补：matlab求矩阵A的LU分解：rref（A）

1.3.3 线性方程组的解

在行变换的基础上加上交换行，化简后的矩阵为:

[\begin{matrix} I & F \\ 0 & 0 \end{matrix}]

$\begin{bmatrix}I&F\\0&0\end{bmatrix}$ 其中I为单位矩阵，F是自由变元的矩阵
特解：

A X_{b} = b ， 平 移 向 量 ， 将 零 空 间 移 离 原 点

$AX_b = b，平移向量，将零空间移离原点$
通解：

A (X_{b} + X_{n u l l}) = b ， X_{n u l l} 为 零 空 间

$A(X_b+X_{null}) = b，X_{null}为零空间$

1.4 Gram-Schmidt 正交化

q_{i}^{T} q_{j} = {\begin{cases} 0 & i \neq j \\ 1 & i = j \end{cases}

$q_i^Tq_j=\begin{cases}0&i\neq j\\1& i=j \\\end{cases}$

Q = [\begin{matrix} q_{1}, . ., q_{n} \end{matrix}], 则 Q^{T} Q = I

$Q=\begin{bmatrix}q_1,..,q_n\end{bmatrix}, 则Q^TQ = I$
例：

Q_{1} = \frac{1}{2} [\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & - 1 & 1 & - 1 \\ 1 & 1 & - 1 & - 1 \\ 1 & - 1 & - 1 & 1 \end{matrix}], Q_{2} = [\begin{matrix} c o s (θ) & - s i n (θ) \\ a i n (θ) & c o s (θ) \end{matrix}]

$Q_1=\frac{1}{2}\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{bmatrix},Q_2=\begin{bmatrix}cos(\theta)&-sin(\theta)\\ain(\theta)&cos(\theta)\end{bmatrix}$

步骤	说明
单位化	$q_1=\frac{a_1}{\|\|a_1\|\|},q_2=\frac{b_1}{\|\|b_1\|\|},...$
正交化	$a=q_1,b=q_2-\frac{a^{T}b}{a^{T}a}a,...$
整理	$Q = \begin{bmatrix}a&b&..\end{bmatrix}（A=QR，其中R=Q^TA为下三角矩阵$ ）

注1：Q可以不是方阵，如果是方阵则 $Q^{-1}=Q^{T}$

注2：Fourier变换基于正交基 $[sin(t),cos(t),..]或[e^t,e^{it},..]$

1.5 分块矩阵

矩阵可以分块计算

1.6 Markov矩阵

定义：所有元素都不小于0，每列和为1。
性质： $\lambda_1 =1，|\lambda_i| < 1(i\neq1)$
用途：可以用于表示人口的迁移。

2 矩阵的逆

2.1 逆矩阵定义

$如果AB = BA = I，则B为A的逆矩阵，记为A^{-1}$

等价命题
A可逆
AX = 0只有零解
A与I等价
A可以表示成有限个初等矩阵的乘积

2.2 Gass-Jordan

solve more equations at once：
$(A|I) \xrightarrow{初等行变换} (I|A^{-1})$

$A可逆的充要条件为Ax = b有唯一解 x = b/A = A^{-1}b$

2.3 伪逆（sudo inverse）

伪逆	条件1	条件2	形式	结论
left inverse	r=n	$N(A)=0$	$(A^TA)^{-1}A^T$	0或1个解
right inverse	r=m	$N(A^T)=0$	$A^T(AA^T)^{-1}$	多解，n-m个自由变量

$A(A^TA)^{-1}A^T$ 是在列空间中的投影
$A^T(AA^T)^{-1}A$ 是在行空间中的投影

2.4 奇异值分解（SVD）

任何矩阵A都可以分解成： $A = U\Sigma V^T$ 其中 $\Sigma$ 为对角矩阵
$AA^T = U \Sigma \Sigma^TU^T=UDU^T$
$A^TA = V \Sigma^T \Sigma V^T=VWV^T$
$D_{m \times m}=\begin{bmatrix} \sigma_1^2&0&0&.\\0&.&0&. \\0&0&\sigma_k^2&.\\.&.&.&0\end{bmatrix}，W_{n \times n}=\begin{bmatrix} \sigma_1^2&0&0&.\\0&.&0&. \\0&0&\sigma_k^2&.\\.&.&.&0\end{bmatrix}$
对应的逆为： $A^+=V \Sigma^+U^T，\Sigma^+=\begin{bmatrix} \frac{1}{\sigma_1}&0&0&.\\0&.&0&. \\0&0&.\frac{1}{\sigma_k}&.\\.&.&.&0\end{bmatrix}$

3 线性空间

3.1 线性相关和张成

定义	说明	例子
向量空间	< V，+，*>是定义了加法和数乘的代数系统	过原点直线，过原点平面
线性空间	满足叠加性：加性+齐性	$f(ax+by)=af(x)+bf(y)$
线性无关	不能互相表示的向量构成的集合	笛卡尔坐标轴
张成（span）	一组向量的全部线性组合的集合
基（base）	张成整个空间V的线性无关向量组称为V的基	(1,0,0,…),(0,1,0,…),..
维度（dimention）	基的长度（或基的个数）

注：0向量是所有向量空间的子集

注：向量空间的交是向量空间，并不一定是

3.2 四个空间

名称	说明
列空间（column space）	矩阵列向量张成的空间
零空间（null space）	$Ax=0$ 的X的解构成的空间，记 $N(A)$
行空间（转置的列空间）	矩阵行向量张成的空间
转置零空间（左零空间）	$A^{T}y = y^{T}A = 0$ ，记 $N(A^T)$

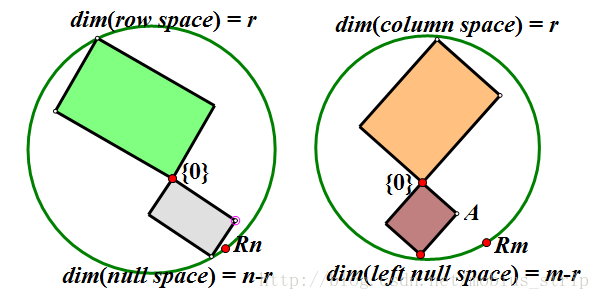
这里写图片描述
如图row space 与 N(A) 正交补，column space 与 $N(A^{T})$ 正交补，row space与column space 构成双射，其他部分都是零空间。

定理：dim（V）= dim（N）+dim（值域）

3.3 线性映射

每个矩阵 $A_{m \times n}$ 对应一个从 $R^m$ 到 $R^n$ 的线性映射，我们一般想要对矩阵A进行化简（特征值构成的对角矩阵），得到不同的基下的表示（分解成独立的子空间），可以简化问题或者看到问题的本质。

注：线性映射到矩阵的映射也是线性映射

3.3.1 特征值和特征向量（解耦、对角化）

特征向量在矩阵A的变化下只会出现缩放，不会出现方向变化：
$Ax=\lambda x，\lambda =0时，Ax=0，对应的x确定零空间N(A)$
求解： $Ax=\lambda x \rightarrow (A-\lambda I)x=0$
x不为0时，有 $|A-\lambda I|=0，得到特征方程，x_i为A-\lambda_iI的零空间。$

注： $\begin{cases}Ax=\alpha x \\Bx=\beta x \end{cases} \nrightarrow (A+B)x=(\alpha + \beta)x，对应的特征向量不同$

3.3.2 特殊的特征值

矩阵	特征值	例子
负对阵	$\lambda 为虚数$	$旋转矩阵\begin{bmatrix}0&-1\\1&0 \end{bmatrix}，\lambda_1 = i，\lambda_2 =-i，v_1 = \begin{bmatrix}i\\-1\end{bmatrix}，v_2=\begin{bmatrix}i\\1\end{bmatrix}$
正对称	$\lambda 为实数，不同特征值的特征向量正交$
畸形	$\lambda 和正交向量不够n个$	$\begin{bmatrix}0&1\\0&0 \end{bmatrix}，\lambda = 1，v=\begin{bmatrix}1\\0\end{bmatrix}$

3.3.3 特征值性质

$\sum_{i=1}^n \lambda_i=\sum_{i=1}^n a_{ii}$
$\prod_{i=1}^n \lambda_i=detA$

3.3.4 QR法

利用QR分解迭代求解特征值：
$A_i = Q_iR_i$
$R_iQ_i=A_{i+1}$
迭代数次得到对角线矩阵，其中值为特征值

3.3.5 矩阵的多项式

$f(A) = a_1A^k+...+a_1A+a_0I$
$f(\lambda) = a_1\lambda^k+...+a_1\lambda+a_0$

性质：f(A)g(A) = g(A)f(A)

4 行列式

4.1 定义

d e t A = | \begin{matrix} a_{11} & a_{12} & . . . & a_{1 n} \\ a_{21} & a_{22} & . . . & a_{2 n} \\ . & . & . \\ a_{n 1} & a_{n 2} & . . . & a_{n n} \end{matrix} |

$det A = \left| \begin{matrix} a_{11}&a_{12}&...&a_{1n}\\ a_{21}&a_{22}&...&a_{2n}\\ .&.&&.\\ a_{n1}&a_{n2}&...&a_{nn}\\ \end{matrix} \right|$

当 n = 1 时 ， d e t A = a_{11}

$当n=1时，detA = a_{11}$

当 n \geq 2 时 ， d e t A = a_{11} A_{11} + a_{12} A_{12} + . . . a_{1 n} A_{1 n}, A_{i j} = (- 1)^{i + j} M_{i j}

$当n \geq 2时，detA = a_{11}A_{11}+a_{12}A_{12}+...a_{1n}A_{1n},A_{ij} = (-1)^{i+j}M_{ij}$

其 中 A_{i j} 称 为 余 子 式 ， M_{i j} 为 代 数 余 子 式 。

$其中A_{ij}称为余子式，M_{ij}为代数余子式。$

4.2 对比矩阵和行列式

行列式	矩阵
数	数表
$D_n$	$A_{m \times n}$
\| \|	(),[]

4.3 行列式的性质

ID	性质	推论
1	$detI = 1(放缩)$	$detA=0为奇异$
2	行列式按任意一行展开，其值相等： $detA = a_{i1}A_{i1}+...+a_{in}A_{in}$	$detA某一行全为0\Rightarrow detA=0$
3	$detA中某两行对应位置元素相等\Rightarrow detA=0$
4	$\| \begin{matrix} a_{11} & . . & a_{1 n} \\ . & . & . \\ b_{i 1} + c_{i 1} & . . & b_{i n} + c_{i n} \\ . & . & . \\ a_{n 1} & . . & a_{n n} \end{matrix} \| = \| \begin{matrix} a_{11} & . . & a_{1 n} \\ . & . & . \\ b_{i 1} & . . & b_{i n} \\ . & . & . \\ a_{n 1} & . . & a_{n n} \end{matrix} \| + \| \begin{matrix} a_{11} & . . & a_{1 n} \\ . & . & . \\ c_{i 1} & . . & c_{i n} \\ . & . & . \\ a_{n 1} & . . & a_{n n} \end{matrix} \|$ $\left\|\begin{matrix}a_{11}&..&a_{1n}\\.&.&.\\b_{i1}+c_{i1}&..&b_{in}+c_{in}\\.&.&.\\a_{n1}&..&a_{nn}\\\end{matrix} \right\|=\\\left\|\begin{matrix}a_{11}&..&a_{1n}\\.&.&.\\b_{i1}&..&b_{in}\\.&.&.\\a_{n1}&..&a_{nn}\\\end{matrix} \right\|+\left\|\begin{matrix}a_{11}&..&a_{1n}\\.&.&.\\c_{i1}&..&c_{in}\\.&.&.\\a_{n1}&..&a_{nn}\\\end{matrix} \right\|$
5	$将A的某一行元素全乘以k得到detA_1=kdetA$	$将某一行的k倍加到其他行detA不，交换两行detA变号，某两行元素对应成比例则detA=0$
6	$det(AB)=detA*detB$	$det(A^T)=detA$

4.4 伴随矩阵

$A^{-1}=\frac{C^T}{detA}$
$C^T$ 为伴随矩阵， $c_{ij}为对应的余子式$
验证：

[\begin{matrix} a_{11} & a_{12} & . & a_{1 n} \\ a_{21} & a_{22} & . & a_{2 n} \\ . & . & . \\ a_{n 1} & a_{n 2} & . & a_{n n} \end{matrix}] [\begin{matrix} c_{11} & c_{12} & . & c_{1 n} \\ c_{21} & c_{22} & . & c_{2 n} \\ . & . & . \\ c_{n 1} & a_{n 2} & . & c_{n n} \end{matrix}] = [\begin{matrix} d e t A & 0 & . & 0 \\ 0 & d e t A & . & 0 \\ . & . & . \\ 0 & 0 & . & d e t A \end{matrix}] = d e t A \cdot I

$\begin{bmatrix}a_{11}&a_{12}&.&a_{1n}\\a_{21}&a_{22}&.&a_{2n}\\ .&.&&.\\a_{n1}&a_{n2}&.&a_{nn} \end{bmatrix} \begin{bmatrix}c_{11}&c_{12}&.&c_{1n}\\c_{21}&c_{22}&.&c_{2n}\\ .&.&&.\\c_{n1}&a_{n2}&.&c_{nn} \end{bmatrix} = \begin{bmatrix}detA&0&.&0\\0&detA&.&0\\ .&.&&.\\0&0&.&detA \end{bmatrix}=detA \cdot I$

4.5 集合意义

行列式的值为向量组维成的超体的体积，特征向量方向的缩放比为对应的特征值。

5 应用

5.1 电路

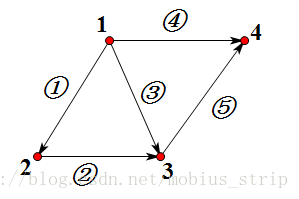
这里写图片描述
令矩阵A的行为边，列为节点，出度为-1，入度为1，x为顶点（电压），y为边（电流）。

5.1.1 电压

A x = [\begin{matrix} - 1 & 1 & 0 & 0 \\ 0 & - 1 & 1 & 0 \\ - 1 & 0 & 1 & 0 \\ - 1 & 0 & 0 & 1 \\ 0 & 0 & - 1 & 1 \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{matrix}] = C [\begin{matrix} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ y_{5} \end{matrix}]

$Ax= \begin{bmatrix}-1&1&0&0\\0&-1&1&0\\-1&0&1&0\\-1&0&0&1\\0&0&-1&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\\x_4\end{bmatrix} = C\begin{bmatrix}y_1\\y_2\\y_3\\y_4\\y_5\end{bmatrix}$
左侧为压降矩阵，右侧为欧姆定理，C为电阻矩阵。

5.1.2 电流

A^{T} y = [\begin{matrix} - 1 & 0 & - 1 & - 1 & 0 \\ 1 & - 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & - 1 \\ 0 & 0 & 0 & 1 & 1 \end{matrix}] [\begin{matrix} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ y_{5} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix}]

$A^Ty= \begin{bmatrix}-1&0&-1&-1&0\\1&-1&0&0&0\\0&1&1&0&-1\\0&0&0&1&1\end{bmatrix}\begin{bmatrix}y_1\\y_2\\y_3\\y_4\\y_5\end{bmatrix} = \begin{bmatrix}0\\0\\0\\0\end{bmatrix}$
基尔霍夫定律，节点电流和为0；加入电流源

f = A^{T} y = A^{T} C A X ， A^{T} C A 为 对 称 矩 阵

$f=A^Ty=A^TCAX，A^TCA为对称矩阵$ 。

5.2 投影（projection）

$求解Ax=b，b不属于A的列向量张成的空间，此时求解距离最小的最优解A \hat x =p，p是b在a方向的投影。$

5.2.1 一维投影

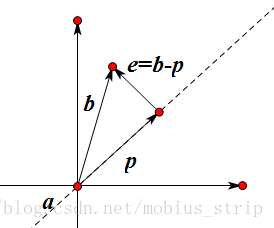
这里写图片描述
设 $\vec{p}=x\vec{a}，其中x为比例系数，故求解x即可。因为\vec{e}与\vec{p}正交时e的模最小，故：$
$\vec{e} \cdot \vec{p}=\vec{a}^{T}(\vec{b}-\vec{p})=\vec{a}^{T}(\vec{b}-x\vec{a})=0$
$x = \frac{a^Tb}{a^Ta}，p = ax = a\frac{a^Tb}{a^Ta} = \frac{aa^T}{a^Ta}b = Pb$

5.2.2 高维投影

因为e与A正交，故e $\in N(A^T)$
定义： $p = x_1a_1 + .. + x_ka_k = A x$
正交： $a_i^Te_i=a_i^T(b_i-Ax_i) = 0$
$p = Ax = A(A^TA)^{-1}A^Tb = Pb$

5.2.3 投影性质

投影矩阵（P）的性质
$P^T=P$
$P^2=P$
$I=P+E,（b-p=e=Eb）$

5.3 最小二乘

数据拟合，求解到已知点距离和最小的目标曲线。
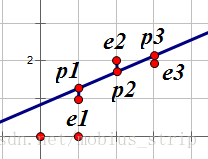
这里写图片描述

5.3.1 利用矩阵求解

设直线为C+Dx=y，带入三点坐标：

[\begin{matrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{matrix}] [\begin{matrix} C \\ D \end{matrix}] = [\begin{matrix} 1 \\ 2 \\ 2 \end{matrix}]

$\begin{bmatrix}1&1\\1&2\\1&3\end{bmatrix}\begin{bmatrix}C\\D\end{bmatrix}=\begin{bmatrix}1\\2\\2\end{bmatrix}$

A^{T} A \hat{x} = A^{T} b ， \hat{x} 为 最 小 二 乘 解 ， 图 解 如 下 ：

$A^TA \hat x = A^Tb，\hat x 为最小二乘解，图解如下：$
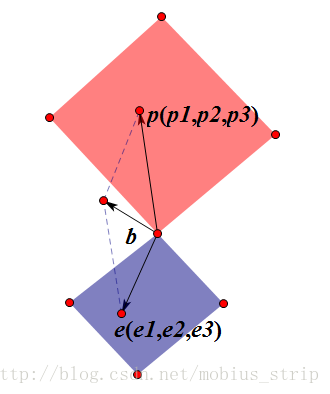
这里写图片描述

5.3.2 利用导数求解

$min {||Ax-b||}^2={||e||}^2=e_1^2+e_2^2+e_3^2$
$f(C,D)={(C+D-1)}^2+{(C+2D-2)}^2+{(C+3D-2)}^2$
$\frac{\partial f}{\partial C} = 0 \rightarrow 6C+4D=0$
$\frac{\partial f}{\partial D} = 0 \rightarrow 3C+6D=0$

微分方程 5.4

$Ax=\lambda x \rightarrow AS=\Lambda S \rightarrow A = S^{-1} \Lambda S$
$S为特征向量构成的矩阵，\Lambda 为特征值构成的矩阵。上面公式可以简化矩阵求幂。$

5.4.1 通解

方程	通解
$U_{k+1}=AU_k$	$U_k=C_1 \lambda^k x_x +..$
$\frac{du}{dt}=Au$	$u(t)=C_1e^{\lambda_1t}+..$

5.4.2 稳定性

线代控制理论用矩阵表示系统，如上面第二种微分方程，指数中的虚部代表震荡，实部影响稳定性。

$\lambda$	稳定性
所有 $\lambda_i\leq$ 1	李雅普诺夫稳定（不发散）
所有 $\lambda_i=$ 1	渐进稳定（随着时间收敛到0）
存在 $\lambda_i>$ 1	不稳定

5.5 基变换和图像压缩

图片（512x512 pixel） $\xrightarrow{JPEG}{}$ 64block（8x8 pixel） $\xrightarrow{基变换}{}$ 系数c $\xrightarrow{压缩}{} \hat c（许多0）$

变换基	举例	性质
standard	$\begin{bmatrix}1\\0\\0\\0\\0\\0\\0\\0\end{bmatrix}$ $\begin{bmatrix}0\\1\\0\\0\\0\\0\\0\\0\end{bmatrix}$ .. $\begin{bmatrix}0\\0\\0\\0\\0\\0\\0\\1\end{bmatrix}$	效果不好
better	低频（全同）： $\begin{bmatrix}1\\1\\1\\1\\1\\1\\1\\1\end{bmatrix}$ 上下相反： $\begin{bmatrix}1\\1\\1\\1\\-1\\-1\\-1\\-1\end{bmatrix}$ ..高频（棋盘）： $\begin{bmatrix}0\\0\\0\\0\\0\\0\\0\\1\end{bmatrix}$	不好求逆
Fourier	$\begin{bmatrix}1\\1\\1\\1\\1\\1\\1\\1\end{bmatrix}$ $\begin{bmatrix}1\\\omega\\\omega^2\\\omega^3\\\omega^4\\\omega^5\\\omega^6\\\omega^7\end{bmatrix}$ .. $\begin{bmatrix}1\\\omega^7\\\omega^{14}\\\omega^{21}\\\omega^{28}\\\omega^{35}\\\omega^{42}\\\omega^{49}\end{bmatrix}$	效果好，好求逆
简化小波	$\begin{bmatrix}1\\1\\1\\1\\1\\1\\1\\1\end{bmatrix}$ $\begin{bmatrix}1\\1\\1\\1\\-1\\-1\\-1\\-1\end{bmatrix}$ $\begin{bmatrix}1\\1\\-1\\-1\\0\\0\\0\\0\end{bmatrix}$ $\begin{bmatrix}0\\0\\0\\0\\1\\1\\-1\\-1\end{bmatrix}$ $\begin{bmatrix}1\\-1\\0\\0\\0\\0\\0\\0\end{bmatrix}$ $\begin{bmatrix}0\\0\\1\\-1\\0\\0\\0\\0\end{bmatrix}$ $\begin{bmatrix}0\\0\\0\\0\\1\\-1\\0\\0\end{bmatrix}$ $\begin{bmatrix}0\\0\\0\\0\\0\\0\\1\\-1\end{bmatrix}$	效果好，好求逆

线性代数笔记