\(\fbox{例1}\)利用直线参数方程的参数的几何意义解题
在极坐标系中，已知圆\(C\)的圆心\(C(\sqrt{2}，\cfrac{\pi}{4})\)，半径\(r=\sqrt{3}\)，
（1）求圆\(C\)的极坐标方程。
（2）若\(\alpha \in[0，\cfrac{\pi}{4}]\)，直线\(l\)的参数方程为\(\begin{cases} x=2+cos\alpha\cdot t \\y=2+sin\alpha\cdot t \end{cases}(t为参数)\) ，
直线\(l\)交圆\(C\)于\(A、B\)两点，求弦长\(|AB|\)的取值范围。
解：（1）圆\(C\)的圆心\(C(\sqrt{2}，\cfrac{\pi}{4})\)，得\(C\)的直角坐标为\((1,1)\)，
所以圆\(C\)的直角坐标方程为\((x-1)^2+(y-1)^2=3\)，由\(x=\rho cos\theta，y=\rho sin\theta\)得到，
圆\(C\)的极坐标方程为\(\rho^2-2\rho cos\theta-2\rho sin\theta-1=0\)。
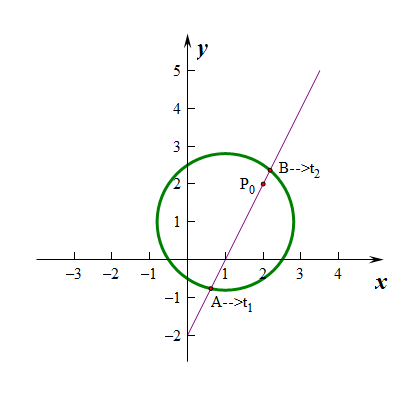
（2）将 \(\begin{cases} x=2+cos\alpha\cdot t \\y=2+sin\alpha\cdot t \end{cases}(t为参数)\)，
代入圆\(C\)的直角坐标方程为\((x-1)^2+(y-1)^2=3\)，
得到\(t^2+2(cos\alpha+sin\alpha)t-1=0\)，
则有\(\Delta= 4(cos\alpha+sin\alpha)^2+4>0\)，
设\(A、B\)两点对应的参数分别为\(t_1，t_2\)，
则由韦达定理可知，\(t_1+t_2=2(cos\alpha+sin\alpha)，t_1\cdot t_2= -1\)
所以弦长\(|AB|=|t_1-t_2|=\sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{8+4sin2\alpha}\)，
由于\(\alpha \in[0,\cfrac{\pi}{4}]\)，所以\(sin2\alpha\in[0，1]\)，\(8+4sin2\alpha\in[8，12]\)，
所以弦长\(|AB|\in[2\sqrt{2}，2\sqrt{3}]\)。
\(\fbox{例2}\)
在极坐标系中，曲线\(C\)的极坐标方程为\(\rho^2=\cfrac{3}{1+2sin^2\theta}\)和点\(R(2\sqrt{2}，\cfrac{\pi}{4})\)
⑴将曲线\(C\)的极坐标方程化为直角坐标方程；
⑵设点\(P\)为曲线\(C\)上一动点，矩形\(PQRS\)以\(PR\)为其对角线，且矩形的一边垂直于极轴，求矩形\(PQRS\)的周长的最小值及此时点\(P\)的直角坐标。
分析：⑴将曲线\(C\)的极坐标方程为\(\rho^2=\cfrac{3}{1+2sin^2\theta}\)变形为\(\rho^2+2(\rho sin\theta)^2=3\)，
即\(x^2+y^2+2y^2=x^2+3y^2=3\)，也就是\(\cfrac{x^2}{3}+y^2=1\)；
⑵作出大致图像，课件地址：https://www.desmos.com/calculator/dhitlnlyw7
我们可以作出点\(P\)的坐标\(P(\sqrt{3}cos\theta，sin\theta)\)，
那么点\(Q(2，sin\theta)\)，点\(R(2，2)\)，则\(|PQ|=2-\sqrt{3}cos\theta\)，\(|RQ|=2-sin\theta\)，
则\(|PQ|+|RQ|=4-2sin(\theta+\cfrac{\pi}{3})\)，
当\(\theta=\cfrac{\pi}{6}\)时，\((|PQ|+|RQ|)_{min}=2\)，所以矩形\(PQRS\)的周长的最小值为4，
此时点\(P\)的坐标为\((\sqrt{3}cos\cfrac{\pi}{6}，sin\cfrac{\pi}{6})\)，即\((\cfrac{3}{2}，\cfrac{1}{2})\)。
\(\fbox{例3}\)
在直角坐标系\(xOy\)中，直线\(l\)的参数方程为\(\begin{cases} x=3-\cfrac{\sqrt{2}}{2}\cdot t \\ y=\sqrt{5}+\cfrac{\sqrt{2}}{2}\cdot t \end{cases}(t为参数)\)，在极坐标系中圆\(C\)的方程为\(\rho=2\sqrt{5}sin\theta\).
⑴求圆的直角坐标方程；
⑵设圆\(C\)与直线\(l\)交于点\(A、B\)，若点\(P\)的坐标为\((3，\sqrt{5})\)，求\(|PA|+|PB|\).
分析： ⑴简解，\(x^2+(y-\sqrt{5})^2=5\)
⑵思路一：将直线和圆的直角坐标方程联立，求得交点\(A、B\)的坐标，能否用两点间的坐标公式求解\(|PA|+|PB|\).
思路二：利用直线参数方程的参数的几何意义，
将直线的参数方程\(\begin{cases} x=3-\cfrac{\sqrt{2}}{2}\cdot t \\ y=\sqrt{5}+\cfrac{\sqrt{2}}{2}\cdot t \end{cases}(t为参数)\)代入圆的直角坐标方程，
得到\((3-\cfrac{\sqrt{2}}{2}\cdot t)^2+(\sqrt{5}+\cfrac{\sqrt{2}}{2}\cdot t -\sqrt{5})^2=5\)整理为\(t^2-3\sqrt{2}t+4=0\)，
由于\(\Delta >0\)，故可设点\(A、B\)分别对应参数\(t_1，t_2\)，
则\(\begin{cases} t_1+ t_2=3\sqrt{2} \\ t_1\times t_2=4 \end{cases}\)，
由此可以看出\(t_1>0，t_2>0\)，故\(|PA|=t_1，|PB|=t_2\)，所以\(|PA|+|PB|=3\sqrt{2}\).
问题：一定有\(|PA|+|PB|=|AB|\)这个结论吗？为什么？
课件地址：https://www.desmos.com/calculator/eqo1ssqog8
\(\fbox{例4}\)在直角坐标系\(xOy\)中，直线\(l\)是过定点\(P(4，2)\)且倾斜角为\(\alpha\)的直线；在极坐标系中，曲线\(C\)的极坐标方程为\(\rho=4cos\theta\).
⑴写出直线\(l\)的参数方程，并将曲线\(C\)的极坐标方程化为直角坐标方程；
⑵若曲线\(C\)与直线\(l\)相交于不同的两点\(M、N\)，求\(|PM|+|PN|\)的取值范围.
分析：⑴直线\(l\)的参数方程为\(\begin{cases} x=4+cos\alpha\cdot t \\ y=2+sin\alpha\cdot t \end{cases}(t为参数)\)，曲线\(C\)的直角坐标方程为\(x^2+y^2=4x\)；
⑵课件地址：https://www.desmos.com/calculator/uwny2tygwe
法1：几何法，不具备通用性，比如圆锥曲线，
法2：通法，将\(\begin{cases} x=4+cos\alpha\cdot t \\ y=2+sin\alpha\cdot t \end{cases}(t为参数)\)代入\(C：x^2+y^2=4x\)，
得到\(t^2+4(sin\alpha+cos\alpha)t+4=0\)，
则必然满足条件\(\begin{cases} &\Delta=16(sin\alpha+cos\alpha)^2-16>0\\ &t_1+t_2=-4(sin\alpha+cos\alpha)\\&t_1\cdot t_2=4\end{cases}(t为参数)\)，
由此得到\(sin\alpha\cdot cos\alpha>0\)，又\(\alpha\in [0，\pi)\)，
故压缩范围得到\(\alpha\in (0，\cfrac{\pi}{2})\)，
则\(|PM|+|PN|=|t_1|+|t_2|=-(t_1+t_2)=4(sin\alpha+cos\alpha)=4\sqrt{2}sin(\alpha+\cfrac{\pi}{4})\)，
由\(\alpha \in (0，\cfrac{\pi}{2})\) ，得到\(\alpha+\cfrac{\pi}{4}\in (\cfrac{\pi}{4}，\cfrac{3\pi}{4})\)，
则\(\cfrac{\sqrt{2}}{2}< sin(\alpha+\cfrac{\pi}{4}) \leq 1\)，
故$ 4\sqrt{2}\times \cfrac{\sqrt{2}}{2}< 4\sqrt{2}\cdot sin(\alpha+\cfrac{\pi}{4}) \leq 4\sqrt{2}\times 1 $，
即就是$|PM|+|PN|\in(4，4\sqrt{2}] $.
(2016全国卷Ⅱ第23题高考真题)
【选修4-4：坐标系与参数方程】在直角坐标系\(xOy\)中，圆\(C\) 的方程为\((x+6)^2+y^2=25\)．
(1)以坐标原点为极点，\(x\)轴的正半轴为极轴建立极坐标系，求\(C\)的极坐标方程。
分析：由于极坐标方程中只有\(\rho\)和\(\theta\)，
故只要将\(x=\rho\cdot cos\theta\)和\(y=\rho\cdot sin\theta\)代入圆\(C\)的直角坐标方程为\((x+6)^2+y^2=25\)，
整理可得\(\rho^2+12\rho cos\theta+11=0\)。
(2)直线\(l\)的参数方程为\(\begin{cases} x=t\cdot cos\alpha \\ y=t\cdot sin\alpha \end{cases}(t为参数)\)，
\(l\)与\(C\)交于A、B两点，\(|AB|=\sqrt{10}\)，求直线\(l\)的斜率。
【法1】参数方程法，
分析：本题目的求解要用到直线的参数方程的几何意义。
将直线\(l\)的参数方程代入圆\(C\)的直角坐标方程，
化简整理为\(t^2+12t cos\alpha+11=0\)，可设点\(A、B\)分别对应参数\(t_1，t_2\)，
则\(\begin{cases} t_1+ t_2=-12cos\alpha \\ t_1\times t_2=11\end{cases}\)，
\(|AB|=|t_1-t_2|= \sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{10}\)，
解得\(cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}\)，
又由图可知\(\alpha\in [0，\pi)\)，故\(cos\alpha=\pm\cfrac{\sqrt{6}}{4}\)，
则有\(sin\alpha=\cfrac{\sqrt{10}}{4}\)
故\(tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\cfrac{\sqrt{10}}{4} }{\pm\cfrac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}\)。
故直线\(l\)的斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
【法2】极坐标系法，
圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\theta+11=0\)。
将直线的参数方程两式相除得到，\(y=tan\alpha x\)，即\(y=kx\)，
则直线的极坐标方程为\(\theta=\alpha(\rho\in R)\)
将直线的极坐标方程代入圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\theta+11=0\)，
得到圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\alpha+11=0\)，
设点\(A\)的极坐标方程为\((\rho_1，\alpha)\)，点\(B\)的极坐标方程为\((\rho_2，\alpha)\)，
则\(\rho_1+\rho_2=-12cos\alpha\)，\(\rho_1\cdot \rho_2=11\)，
由\(|AB|=|\rho_1-\rho_2|= \sqrt{(\rho_1+\rho_2)^2-4\rho_1\rho_2}=\sqrt{10}\)，
解得\(cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}\)，
又由图可知\(\alpha\in [0，\pi)\)，故\(cos\alpha=\pm\cfrac{\sqrt{6}}{4}\)，
则有\(sin\alpha=\cfrac{\sqrt{10}}{4}\)
故\(tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\cfrac{\sqrt{10}}{4} }{\pm\cfrac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}\)。
故直线\(l\)的斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
【法3】平面几何法，
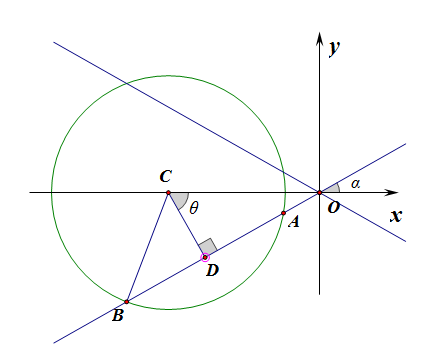
如图所示，这样的直线应该有两条，且其斜率互为相反数，
现重点求解图中的直线\(AB\)的斜率，
在\(Rt\Delta BCD\)中，半径为\(BC=5\)，半弦长为\(BD=\cfrac{\sqrt{10}}{2}\)，
利用勾股定理求得，弦心距\(CD=\cfrac{3\sqrt{10}}{2}\)
在\(Rt\Delta OCD\)中，\(OC=6\)，\(CD=\cfrac{3\sqrt{10}}{2}\)
求得\(cos\angle OCD=cos\theta=\cfrac{\sqrt{10}}{4}\)
从而\(sin\alpha=\cfrac{\sqrt{10}}{4}\)，\(cos\alpha=\cfrac{\sqrt{6}}{4}\)，
即\(k=tan\alpha=\cfrac{\sqrt{10}}{\sqrt{6}}=\cfrac{\sqrt{15}}{3}\)，
故满足条件的直线\(AB\)有两条，其斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
(2017全国卷Ⅱ文理同题，第22题高考真题)【选修4-4：坐标系与参数方程】在直角坐标系\(xOy\)中，以坐标原点为极点，\(x\)轴的正半轴为极轴建立极坐标系，曲线\(C_1\) 的极坐标方程为\(\rho cos\theta=4\) ．
（1）M为曲线\(C_1\)上的动点，点P在线段OM上，且满足\(|OM|\cdot|OP|=16\)，求点P的轨迹\(C_2\)的直角坐标方程；
法一：[学生容易想到的解法]
容易化简\(C_1：x=4\)，做出简单的示意图，我们可以令\(M(4,m)、P(x，y)\)，
则由题目可知\(\cfrac{y}{x}=\cfrac{m}{4}\)，即\(m=\cfrac{4y}{x}\)，
又由题目可知满足条件\(|OM|\cdot|OP|=16\)，即\(\sqrt{4^2+m^2}\cdot\sqrt{x^2+y^2}=16\)，
将\(m=\cfrac{4y}{x}\)代入，整理得到\((4^2+\cfrac{16y^2}{x^2})\cdot(x^2+y^2)=256\)，
整理得到\(x^4+2x^2y^2-16x^2+y^4=0\)，最终可以化简为\((x-2)^2+y^2=4(x>0)\)。
- 整个化简过程涉及到坐标变换，这个暂时不做介绍；
2.
课件
\(\fbox{法2}\)直接借助极坐标系来思考运算，
令\(M(\rho，\theta)\)，\(P(\rho_1，\theta)(\rho_1>0)\),有题可知，
点M满足\(C_1\)的方程\(\rho cos\theta=4\) 。则\(\rho=\cfrac{4}{cos\theta}\)，
又\(|OM|=\rho=\cfrac{4}{cos\theta}\)，\(|OP|=\rho_1\)，
又由题目可知\(|OM|\cdot|OP|=\rho\rho_1=16\)，
故\(\rho_1=\cfrac{16}{\rho}=4cos\theta(\rho_1>0)\)，
两边同乘以\(\rho_1\)得到
\(\rho_1^2=4\rho_1 cos\theta\)，
转化为直角坐标方程为\(x^2+y^2=4x(x\neq 0)\)，
即\((x-2)^2+y^2=4(x\neq 0)\)为曲线\(C_2\)的直角坐标方程。
我们必须扭转以直角坐标为桥梁的的求解思路，快速适应在极坐标系下的思维模式。
（2）设点A的极坐标为\((2，\cfrac{\pi}{3})\)，点B在曲线\(C_2\)上，求\(\Delta OAB\)面积的最大值．
法1：直线\(OA\)的方程为\(\sqrt{3}x-y=0\)，点B在曲线\(C_2\)上，故点B的参数坐标为\((2cos\theta+2，2sin\theta)(\theta\in (-\pi，\pi))\)，
(?此处怎么转化，为什么这样转化)
故三角形\(\Delta OAB\)的一条边OA上的高为点B到直线OA的距离
\(h_{OA}=\cfrac{|\sqrt{3}(2cos\theta+2)-2sin\theta|}{\sqrt{(\sqrt{3})^2+1^2}}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|\)
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA|\cdot h_{OA}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|=|2cos(\theta+\cfrac{\pi}{6})+\sqrt{3}|\)，
当\(cos(\theta+\cfrac{\pi}{6})=1\)，即\(\theta=-\cfrac{\pi}{6}\)时，\(S_{max}=2+\sqrt{3}\)。
\(\fbox{法2}\)直接借助极坐标系来思考运算，
点\(A(3，\cfrac{\pi}{2})\)，点\(B(\rho，\alpha)(\alpha\in (-\cfrac{\pi}{2}，\cfrac{\pi}{2}))\)，
又点B满足曲线\(C_2\)的极坐标方程，
故\(|OB|=\rho=4cos\alpha\)，\(\angle AOB=\cfrac{\pi}{3}-\alpha\)，
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA||OB|sin\angle AOB=\cfrac{1}{2}\cdot 2\cdot 4cos\alpha\cdot sin(\cfrac{\pi}{3}-\alpha)\)
\(=4cos\alpha \cdot sin(\cfrac{\pi}{3}-\alpha)=4cos\alpha\cdot(\cfrac{\sqrt{3}}{2}cos\alpha-\cfrac{1}{2}sin\alpha)\)
\(=2\sqrt{3}cos^2\alpha-2sin\alpha\cdot cos\alpha=\sqrt{3}\cdot (1+cos2\alpha)-sin2\alpha=-2sin(2\alpha-\cfrac{\pi}{3})+\sqrt{3}\)，
故当\(2\alpha-\cfrac{\pi}{3}=-\cfrac{\pi}{2}\)，即\(\alpha=-\cfrac{\pi}{12}\)时，\(S_{\Delta OAB}\)取到最大值\(2+\sqrt{3}\)。
(2017全国卷1，文科第22题高考真题)
在直角坐标系\(xOy\)中，曲线\(C\) 的参数方程为\(\begin{cases}x=3cos\theta\\y=sin\theta\end{cases}(\theta为参数)\)，
直线\(l\)参数方程为\(\begin{cases}x=a+4t\\y=1-t\end{cases}(t为参数)\)，
(1)若\(a=-1\)，求\(C\)与\(l\)的交点坐标。
分析：将曲线\(C\)的参数方程转化为直角坐标方程为\(\cfrac{x^2}{9}+y^2=1①\)；
当\(a=-1\)时，将直线消掉参数得到\(x+4y=3②\)，
两式联立，解方程组得到 \(\begin{cases}x=3\\y=0\end{cases}\)
或\(\begin{cases}x=-\cfrac{21}{25}\\y=\cfrac{24}{25}\end{cases}\)，
故交点坐标为\((3，0)或(-\cfrac{21}{25}，\cfrac{24}{25})\)。
(2)若\(C\)上的点到\(l\)的距离的最大值为\(\sqrt{17}\)，求\(a\).
分析：曲线\(C\)上的任意一点\(P(3cos\theta，sin\theta)\)，
将直线\(l\)消掉参数得到\(x+4y-4-a=0\)，
则点P的直线\(l\)的距离为
\(d=\cfrac{|3cos\theta+4sin\theta-4-a|}{\sqrt{17}}\)
\(=\cfrac{|5sin(\theta+\phi)-(4+a)|}{\sqrt{17}}(tan\phi=\cfrac{3}{4})\)；
当\(4+a\ge 0\)时，即\(a\ge -4\)时，取\(sin(\theta+\phi)=-1\)，
\(d_{max}=\cfrac{|-5-a-4|}{\sqrt{17}}=\cfrac{9+a}{\sqrt{17}}=\sqrt{17}\)，解得\(a=8\)；
当\(4+a< 0\)时，即\(a< -4\)时，
取\(sin(\theta+\phi)=1\)，\(d_{max}=\cfrac{|5-a-4|}{\sqrt{17}}=\cfrac{1-a}{\sqrt{17}}=\sqrt{17}\)，解得\(a=-16\)。
综上所述，\(a\)的值为\(8或-16\)。
\(\fbox{例？}\)
已知椭圆\(\cfrac{x^2}{4}+y^2=1\)和点\(A(1，\cfrac{1}{2})\)，点P为椭圆上的一个动点，线段PA的中点为M，求点M的轨迹方程。
法1：相关点法，设线段PA的中点为M\((x，y)\)，点P的坐标为\((x_0，y_0)\)，
由\(\begin{cases}x=\cfrac{x_0+1}{2}\\y=\cfrac{y_0+\frac{1}{2}}{2}\end{cases}\)
得到\(\begin{cases}x_0=2x-1\\y_0=2y-\frac{1}{2}\end{cases}\)，
由点P在椭圆上，得到\(\cfrac{(2x-1)^2}{4}+(2y-\cfrac{1}{2})^2=1\)，
即点M的轨迹方程为\((x-\cfrac{1}{2})^2+4(y-\cfrac{1}{4})^2=1\)。
法2：参数方程法，由椭圆的标准方程得到其参数方程为\(\begin{cases}x=2cos\theta\\y=sin\theta\end{cases}(\theta为参数)\)，
设椭圆上的动点P\((2cos\theta，sin\theta)\)，设线段PA的中点M\((x，y)\)，
则得到点M的参数方程为\(\begin{cases}x=\cfrac{2cos\theta+1}{2}\\y=\cfrac{sin\theta+\cfrac{1}{2}}{2}\end{cases}(\theta为参数)\)，
消参得到\(\cfrac{(2x-1)^2}{4}+(2y-\cfrac{1}{2})^2=1\)，
即点M的轨迹方程为\((x-\cfrac{1}{2})^2+4(y-\cfrac{1}{4})^2=1\)。
\(\fbox{例？}\)
给定椭圆\(\cfrac{x^2}{3}+y^2=1\)和直线\(x+y-8=0\)，已知点P是椭圆上的一个动点，求点P到直线的距离的最小值。
分析：首先易知椭圆和直线没有交点，即二者相离，从而可以考虑用椭圆的参数方程或平行线法求解。
法1、利用椭圆的参数方程，由椭圆方程\(\cfrac{x^2}{3}+y^2=1\)可知，
动点坐标\(P(\sqrt{3}cos\theta，sin\theta)\)，
则点P到直线\(x+y-8=0\)的距离
\(d(\theta)=\cfrac{|\sqrt{3}cos\theta+sin\theta-8|}{\sqrt{2}}=\cfrac{|2sin(\theta+\cfrac{\pi}{3})-8|}{\sqrt{2}}\)，
故当\(sin(\theta+\cfrac{\pi}{3})=1\)时，\(d_{min}=\cfrac{|2-8|}{\sqrt{2}}=3\sqrt{2}\)；
\(sin(\theta+\cfrac{\pi}{3})=-1\)时，\(d_{max}=\cfrac{|-2-8|}{\sqrt{2}}=5\sqrt{2}\)；
【问题】为什么不设点P的坐标为\((x，y)\)而采用参数坐标形式\((\sqrt{3}cos\theta，sin\theta)\)?
前者坐标形式是二元形式，后者是一元形式，故后者简单。
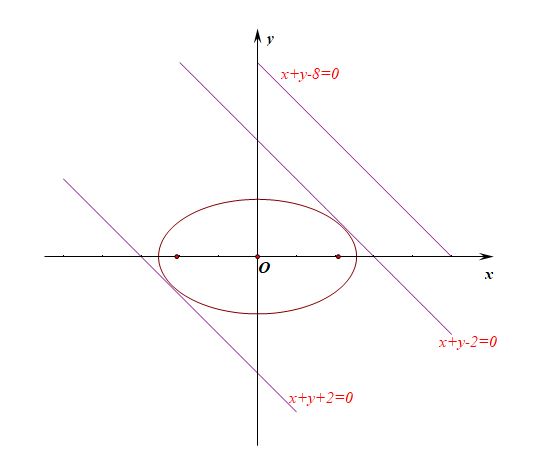
法2、平行线法，设和已知平行且和已知椭圆相切的直线\(x+y+m=0\)，
则由\(x+y+m=0\)和\(\cfrac{x^2}{3}+y^2=1\)，消去\(y\)可得\(4x^2+6mx+3m^2-3=0\)，
由二者相切可知，\(\Delta=36m^2-4\times4(3m^2-3)=0\)，解得\(m=\pm 2\)，
即和椭圆相切的直线有\(x+y-2=0\)和\(x+y+2=0\)，故切点到直线\(x+y-8=0\)的距离就可以用两条平行线间的距离来刻画，
则\(d_{max}=\cfrac{|2-(-8)|}{\sqrt{2}}=5\sqrt{2}\)，\(d_{min}=\cfrac{|-2-(-8)|}{\sqrt{2}}=3\sqrt{2}\)。
1、如果将椭圆换成圆，再求圆上的动点到直线的距离的最值，可以考虑的方法有：
其一，圆的参数方程法；其二，平行线法；其三，几何法，圆心到直线的距离加减半径。
\(\fbox{例8}\)(2016陕西省一检第23题)
在直角坐标系\(xoy\)中，曲线\(C_1：\begin{cases}x=tcos\alpha\\y=tsin\alpha \end{cases}(t为参数，t\neq 0)\)，其中\(0\leq \alpha<\pi\)，在以\(O\)为极点，以\(x\)轴正半轴为极轴的极坐标系中，曲线\(C_2：\rho=2sin\theta\)，\(C_3：\rho=2\sqrt{3}cos\theta\)。
(1)求\(C_2\)与\(C_3\)交点的直角坐标。
分析：曲线\(C_2\)的直角坐标方程为\(x^2+y^2-2y=0\)，曲线\(C_3\)的直角坐标方程为\(x^2+y^2-2\sqrt{3}x=0\)，联立解得\(C_2\)与\(C_3\)交点的直角坐标为\((0，0)\)和\((\cfrac{\sqrt{3}}{2}，\cfrac{3}{2})\)。
(2)若\(C_1\)与\(C_2\)相交于点\(A\)，\(C_1\)与\(C_3\)相交于点\(B\)，求\(|AB|\)的最大值。
分析：在极坐标下思考，曲线\(C_1：\theta=\alpha，0\leq \alpha <\pi\)，曲线\(C_2：\rho=2sin\theta\)，
\(C_3：\rho=2\sqrt{3}cos\theta\)，故\(A(2sin\alpha，\alpha)\)，\(B(2\sqrt{3}cos\alpha，\alpha)\)，
则\(|AB|=|2sin\alpha-2\sqrt{3}cos\alpha|=4|sin(\alpha-\cfrac{\pi}{3})|\)，
当\(sin(\alpha-\cfrac{\pi}{3})=1\)，即\(\alpha=\cfrac{5\pi}{6}\)时，\(|AB|_{max}=4\)。
\(\fbox{例1}\)(宝鸡市二检文理科第22题)
在直角坐标系\(xoy\)中，曲线\(C_1\)的参数方程为\(\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数)\)，
以坐标原点为极点，以\(x\)轴正半轴为极轴，建立极坐标系，曲线\(C_2\)的极坐标方程为\(\rho=2cos\theta\)。
(1)写出曲线\(C_1\)的普通方程和\(C_2\)的直角坐标方程；
(2)设点\(P\) 在\(C_1\)上，点\(Q\) 在\(C_2\)上，且\(\angle POQ=\cfrac{\pi}{2}\)，求三角形\(POQ\)面积的最大值。
分析：(1) 直接给出答案，曲线的普通方程\(C_1：(x-2)^2+y^2=4\)；所求的直角坐标方程\(C_2：(x-1)^2+y^2=1\)；
(2)【法1】极坐标法(本题目命题意图就是想让学生体会极坐标的优越性，从而主动使用极坐标刻画思考或者在极坐标系下运算)，
曲线\(C_1\)的极坐标方程为\(\rho_1=4cos\alpha(\alpha\in(-\cfrac{\pi}{2}，\cfrac{\pi}{2}))\)，
曲线\(C_2\)的极坐标方程为\(\rho_2=2cos\theta(\theta\in(-\cfrac{\pi}{2}，\cfrac{\pi}{2}))\)，
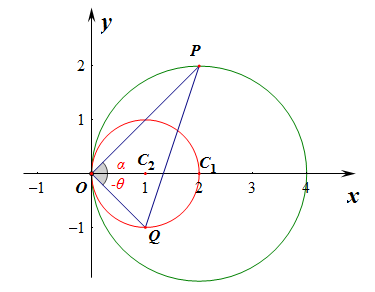
如右图所示，初步分析，当点\(P\)在\(x\)轴上方时，点\(Q\)必在\(x\)轴下方；
当然还会有另一种情形，当点\(P\)在\(x\)轴下方时，点\(Q\)必在\(x\)轴上方；
我们取其中一种做研究，比如点\(P\)在\(x\)轴上方，点\(Q\)在\(x\)轴下方；注意此时点\(Q\)的极角是负值\(-\theta\)，
由于\(\rho_1>0\)，\(\rho_2>0\)，以及\(\angle POQ=\cfrac{\pi}{2}\)可得，
\(\alpha-\theta=\cfrac{\pi}{2}\)，即\(\alpha=\theta+\cfrac{\pi}{2}\)，(顺时针为正，逆时针为负)
则有\(S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|\)
\(=\cfrac{1}{2}\rho_1\rho_2=\cfrac{1}{2}\times 4cos\alpha\times 2cos\theta\)
\(=4cos(\theta+\cfrac{\pi}{2})cos\theta=-4sin\theta cos\theta\)
\(=-2sin2\theta\)，
当\(2\theta=-\cfrac{\pi}{2}\)，即\(\theta=-\cfrac{\pi}{4}\)时，\((S_{\Delta OPQ})_{max}=2\)。
【法2】参数方程法，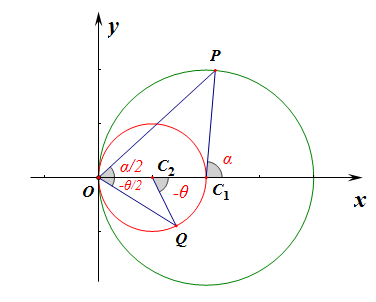
如图所示，曲线\(C_1\)的参数方程是\(\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数，\alpha\in (-\pi，\pi))\)，
曲线\(C_2\)的参数方程是\(\begin{cases}x=1+cos\theta\\y=sin\theta\end{cases}(\theta为参数，\theta\in (-\pi，\pi))\)，
注意参数的含义，\(\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}\)，即\(\alpha=\pi+\theta\)
则有\(S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|\)
\(=\cfrac{1}{2}\sqrt{(2+2cos\alpha)^2+(2sin\alpha)^2}\sqrt{(1+cos\theta)^2+sin^2\theta}\)
\(=\cfrac{1}{2}\sqrt{8(1+cos\alpha)}\sqrt{2(1+cos\theta)}\)
\(=\cfrac{1}{2}\sqrt{8(1-cos\theta)}\sqrt{2(1+cos\theta)}\)
\(=\cfrac{1}{2}\times 4\sqrt{(1-cos\theta)(1+cos\theta)}\)
\(=2\sqrt{1-cos^2\theta}=2|sin\theta|\)
当\(\theta=-\cfrac{\pi}{2}\)时，\((S_{\Delta OPQ})_{max}=2\)。
【变形方法3】参数方程法，曲线\(C_1\)的参数方程是\(\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数，\alpha\in (-\pi，\pi))\)，
曲线\(C_2\)的参数方程是\(\begin{cases}x=1+cos\theta\\y=2sin\theta\end{cases}(\theta为参数，\theta\in (-\pi，\pi))\)，
注意参数的含义，\(\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}\)，即\(\alpha=\pi+\theta\)
由\(\angle POQ=\cfrac{\pi}{2}\)可知，\(k_{OP}k_{OQ}=-1\)，
即\(\cfrac{2sin\alpha}{2+2cos\alpha}\times \cfrac{sin\theta}{1+cos\theta}=-1\)，即\(-sin\alpha sin\theta=(1+cos\alpha)(1+cos\theta)\)
\(S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|\)
\(=\cfrac{1}{2}\sqrt{(2+2cos\alpha)^2+(2sin\alpha)^2}\sqrt{(1+cos\theta)^2+sin^2\theta}\)
\(=\cfrac{1}{2}\sqrt{8(1+cos\alpha)}\sqrt{2(1+cos\theta)}\)
\(=2\sqrt{(1+cos\alpha)(1+cos\theta)}\)
\(=2\sqrt{-sin\alpha sin\theta}\)，
又有\(\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}\)，即\(\alpha=\pi+\theta\)
\(原式=2\sqrt{sin^2\theta}=2|sin\theta|\)，
当\(\theta=-\cfrac{\pi}{2}\)时，\((S_{\Delta OPQ})_{max}=2\)。
【法4】尝试使用均值不等式，待有空思考整理。
设直线\(OP\)的方程为\(y=kx\)，由\(\angle POQ=\cfrac{\pi}{2}\)可得，
直线\(OQ\)的方程为\(y=-\cfrac{1}{k}x\)，
联立\(\begin{cases}(x-2)^2+y^2=4\\y=kx\end{cases}\)，解得\(P(\cfrac{4}{1+k^2}，\cfrac{4k}{1+k^2} )\)，
联立\(\begin{cases}(x-1)^2+y^2=1\\y=-\cfrac{1}{k}x\end{cases}\)，解得$ Q(\cfrac{2k^2}{1+k^2}，\cfrac{-2k}{1+k^2} )$，
\(S_{\Delta POQ}=\cfrac{1}{2}|OP||OQ|=\cfrac{1}{2}\sqrt{(\cfrac{4}{1+k^2})^2+(\cfrac{4k}{1+k^2})^2}\sqrt{(\cfrac{2k^2}{1+k^2})^2+(\cfrac{-2k}{1+k^2})^2}\)
\(=\cfrac{1}{2}\sqrt{\cfrac{16}{1+k^2}}\sqrt{\cfrac{4k^2}{1+k^2}}=\cfrac{4|k|}{1+k^2}=\cfrac{4}{|k|+\frac{1}{|k|}}\leq 2\)。
当且仅当\(|k|=1\)时取到等号。故\((S_{\Delta POQ})_{max}=2\)。
反思：这个解法的优越性体现在只有一个变量\(k\)，那么求最值时就好操作些。
【法5】是否有，待后思考整理。
解后反思：
1、在高中数学中，求某个量(比如面积)的最值时，往往需要先表达出这个量(比如面积)的函数，这样求实际问题的最值就变成了求这个函数模型的最值问题了，这一过程实际就是函数的建模。
1、法1利用极坐标法，这样表达刻画面积时，就只有两个变量\(\alpha\)和\(\theta\)，然后利用两个变量的相互关系，再将变量集中为一个变量，就好求解其最大值了。
2、法2利用参数方程法，在表达刻画面积时，同样只有两个变量\(\alpha\)和\(\theta\)，然后利用两个变量的相互关系，再将变量集中为一个变量，就好求解其最大值了。法2和法3本质接近。
3、正确求解本题目，需要深刻理解极坐标方程的含义和参数方程的含义，尤其是法2对参数的含义更不能弄错了。用到了内外角关系和圆心角和圆周角关系。
4、还有学生想到设\(P(x_1，y_1)\)，$ Q(x_2，y_2)$，这样的思路我没有做尝试，不过能看出来此时是四个变量，这样就难得多了，所以碰到这样的题目我们先需要初步筛选思路。
\(\fbox{例2}\)(2017\(\cdot\)江苏卷)
在平面直角坐标系\(xoy\)中，已知直线\(l\)的参数方程是\(\begin{cases}x=-8+t\\y=\cfrac{t}{2}\end{cases}(t为参数)\)，
曲线\(C\)的参数方程是\(\begin{cases}x=2s^2\\y=2\sqrt{2}s\end{cases}(s为参数)\)，设\(P\)为曲线\(C\)上的动点，
求点\(P\)到直线\(l\)的距离的最小值。
分析：直线\(l\)的直角坐标方程是\(x-2y+8=0\)，曲线\(C\)上的动点\(P\)的坐标\((2s^2，2\sqrt{2}s)\)，
则由点到直线的距离公式可得，
\(d=d(s)=\cfrac{|2s^2-4\sqrt{2}s+8|}{\sqrt{1^2+(-2)^2}}\)
\(=\cfrac{|2(s-\sqrt{2})^2+4|}{\sqrt{5}}\)
当\(s=\sqrt{2}\)时，\(d_{min}=\cfrac{4\sqrt{5}}{5}\)。
解后反思：
1、利用抛物线的参数方程和点线距公式转化为二次函数的最值问题。
2、本题目还可以利用平行线法来求解。
\(\fbox{例3}\)(2017山西太原一模)
在直角坐标系\(xoy\)中，曲线\(C_1\)的参数方程为\(\begin{cases}x=\sqrt{2}cos\phi\\y=sin\phi\end{cases}(\phi为参数)\)，曲线\(C_2：x^2+y^2-2y=0\)。
以原点\(O\)为极点，以\(x\)轴正半轴为极轴，建立极坐标系，射线\(l：\theta=\alpha(\rho\ge 0)\)与曲线\(C_1，C_2\)分别交于点\(A、B\)(均异于原点)
(1)、求曲线\(C_1，C_2\)的极坐标方程；
(2)、当\(0<\alpha<\cfrac{\pi}{2}\)时，求\(|OA|^2+|OB|^2\)的取值范围。
分析：(1)、曲线\(C_1\)的直角坐标方程为\(\cfrac{x^2}{2}+y^2=1\)，极坐标方程为\(\rho^2cos^2\theta+2\rho^2sin^2\theta-2=0\)
曲线\(C_2：x^2+y^2-2y=0\)，极坐标方程为\(\rho=2sin\theta\)。
(2)、法1：极坐标法，设\(A(\rho_1，\theta)\)，\(B(\rho_2，\theta)\)，
注意到\(|OA|^2=\rho_1^2\)，\(|OB|^2=\rho_2^2\)，
联立\(C_1\)与\(l\)的极坐标方程，\(\begin{cases}\theta=\alpha\\ \rho^2cos^2\theta+2\rho^2sin^2\theta-2=0\end{cases}\)，
得到\(|OA|^2=\cfrac{2}{1+sin^2\alpha}\)；
联立\(C_2\)与\(l\)的极坐标方程，\(\begin{cases}\theta=\alpha\\ \rho=2sin\theta\end{cases}\)，
得到\(|OB|^2=4sin^2\alpha\)；
故\(|OA|^2+|OB|^2=\cfrac{2}{1+sin^2\alpha}+4sin^2\alpha\)
\(=\cfrac{2}{1+sin^2\alpha}+4(1+sin^2\alpha)-4\)
令\(1+sin^2\alpha=t\)，则\(t\in (1，2)\)
则\(|OA|^2+|OB|^2=\cfrac{2}{t}+4t-4，t\in (1，2)\)
令\(f(t)=\cfrac{2}{t}+4t-4，t\in (1，2)\)，
\(f'(t)=4-\cfrac{2}{t^2}=\cfrac{4t^2-2}{t^2}\)
当\(1<t<2\)时，\(f'(t)>0\)
用导数可以判断\(t\in (1，2)\)上函数\(f(t)\)单调递增，
故\(|OA|^2+|OB|^2\in (2，5)\)。
法2：参数方程法，如图所示，点\(A\)的参数坐标为\((\sqrt{2}cos\alpha，sin\alpha)\)，
点\(B\)的参数坐标为\((\cos\beta，1+sin\beta)\)，为便于下一步的变量集中，注意到\(\theta+\beta=\cfrac{\pi}{2}\)，
故等价改写点\(B\)的参数坐标为\((\sin\theta，1+cos\theta)\)，且有\(\theta=2(\cfrac{\pi}{2}-\alpha)=\pi-2\alpha\)；
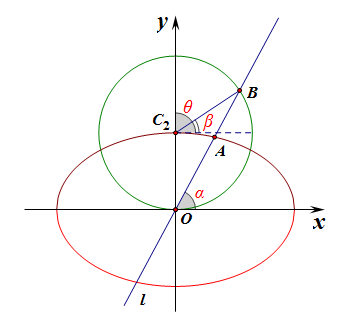
则\(|OA|^2+|OB|^2=(\sqrt{2}cos\alpha)^2+(sin\alpha)^2+(\sin\theta)^2+(1+cos\theta)^2\)
\(=cos^2\alpha+sin^2\alpha+cos^2\alpha+sin^2\theta+1+cos^2\theta+2cos\theta\)
\(=3+cos^2\alpha+2cos(\pi-2\alpha)=3+cos^2\alpha-2cos2\alpha\)
\(=3+cos^2\alpha-2(2cos^2\alpha-1)=5-3cos^2\alpha\)
由于\(0<\alpha<\cfrac{\pi}{2}\)，故\(0<cos^2\alpha<1\)
故\(|OA|^2+|OB|^2\in (2，5)\)。
\(\fbox{例3}\)(图像的变换)
1、已知圆\(C:x^2+y^2=4\)经过\(\phi:\begin{cases}x'=3x\\y'=2y\end{cases}\)变换后所得的曲线\(C'\)是什么？
分析：由\(\phi:\begin{cases}x'=3x\\y'=2y\end{cases}\)得到\(\phi':\begin{cases}x=\cfrac{x'}{3}\\y=\cfrac{y'}{2}\end{cases}\)，
代入圆\(C:x^2+y^2=4\)得到
\((\cfrac{x'}{3})^2+(\cfrac{y'}{2})^2=4\)，
即\(\cfrac{x'^2}{9}+\cfrac{y'^2}{4}=4\)，
即变换后所得的曲线\(C'\)是\(\cfrac{x^2}{36}+\cfrac{y^2}{16}=1\)。
总结：伸缩变换。
2、已知函数\(y=x^2\)经过\(\phi:\begin{cases}x'=x+3\\y'=y\end{cases}\)变换后所得的函数解析式是什么？
分析：由变换\(\phi:\begin{cases}x'=x+3\\y'=y\end{cases}\)得到变换\(\phi':\begin{cases}x=x'-3\\y=y'\end{cases}\)，
代入函数\(y=x^2\)得到\(y'=(x'-3)^2\)，
即变换后的函数为\(y=(x-3)^2\)。
3、将函数\(y=2sin(3x+\cfrac{\pi}{3})\)图像上所有点的横坐标扩大4倍，将纵坐标扩大到原来的2倍，得到的函数解析式是什么？
分析：涉及的变换为\(\phi:\begin{cases}x'=4x\\y'=2y\end{cases}\)，
变形得到变换\(\phi':\begin{cases}x=\cfrac{x'}{4}\\y=\cfrac{y'}{2}\end{cases}\)，
代入函数\(y=2sin(3x+\cfrac{\pi}{3})\)得到函数\(\cfrac{y'}{2}=2sin(3(\cfrac{x'}{4})+\cfrac{\pi}{3})\)，
即函数\(y=4sin(\cfrac{3x}{4}+\cfrac{\pi}{3})\)。
\(\fbox{例4}\)(2017\(\cdot\)全国卷3)
在直角坐标系\(xoy\)中，直线\(l_1\)的参数方程为\(\begin{cases}x=2+t\\y=kt\end{cases}(t为参数)\)，
直线\(l_2\)的参数方程为\(\begin{cases}x=-2+m\\y=\cfrac{m}{k}\end{cases}(m为参数)\)，设\(l_1、l_2\)的交点为\(P\)，
当\(k\)变化时，点\(P\)的轨迹是曲线\(C\)，
(1)、写出曲线\(C\)的普通方程；
(2)、以坐标原点为极点，\(x\)轴正半轴为极轴建立极坐标系，设\(l_3：\rho(cos\theta＋sin\theta)－\sqrt{2}＝0\)，\(M\)为\(l3\)与\(C\)的交点，求点\(M\)的极径．
分析：(1)、用代入消元法，消去参数\(t\)得到直线\(l_1\)的普通方程为\(y=k(x-2)\)，
用代入消元法，消去参数\(m\)得到直线\(l_2\)的普通方程为\(y=\cfrac{1}{k}(x+2)\)，
设点\(P(x，y)\)，则其满足关系\(\begin{cases}y=k(x-2)\\y=\cfrac{1}{k}(x+2)\end{cases}(k可视为参数)\)
故两式相乘，消去参数\(k\)，得到\(y^2=x^2-4\)，
注意\(y\neq 0\)，是因为\(x\neq \pm2\)，否则原式不成立，
故曲线\(C\)的普通方程为\(x^2-y^2=4(y\neq 0)\)；
(2)、直线\(l_3\)即\(x+y=\sqrt{2}\)，和曲线\(C\)的方程\(x^2-y^2=4(y\neq 0)\)联立，
求得\(x=\cfrac{3\sqrt{2}}{2}\)，\(y=-\cfrac{\sqrt{2}}{2}\)，
从而得到点\(M\)的极径\(\rho=\sqrt{x^2+y^2}=\sqrt{5}\)．
\(\fbox{例5}\)(相关点法求轨迹方程)
在直角坐标系\(xoy\)中，以坐标原点为极点，\(x\)轴正半轴为极轴建立极坐标系，直线\(l_1\)的参数方程为\(\begin{cases}x=t\\y=at\end{cases}(t为参数)\)，
曲线\(C_1\)的方程为\(\rho(\rho-4sin\theta)=12\)，定点\(A(6，0)\)，点\(P\)是\(C_1\)上的动点，\(Q\)为\(AP\)的中点，
(1)、求点\(Q\)的轨迹\(C_2\)的直角坐标方程；
(2)、直线\(l\)与曲线\(C_2\)交于\(A、B\)两点，若\(|AB|\ge 2\sqrt{3}\)，求实数\(a\)的取值范围；
分析：(1)【法1】：将曲线\(C_1\)的极坐标方程化为直角坐标方程为\(x^2+y^2-4y=12\)，
设点\(P(x'，y')\)，点\(Q(x，y)\)，由\(Q\)为\(AP\)的中点，
得到\(\begin{cases}x'=2x-6\\y'=2y\end{cases}\)，
代入\(x^2+y^2-4y=12\)，(此方法叫相关点法)
得到点\(Q\)的轨迹\(C_2\)的直角坐标方程为\((x-3)^2+(y-1)^2=4\)；
【法2】：参数方程法，将曲线\(C_1\)的直角坐标方程为\(x^2+y^2-4y=12\)，即\(x^2+(y-2)^2=16\)
化为参数方程得到\(\begin{cases}x=4cos\theta\\y=2+4sin\theta\end{cases}(\theta为参数)\)，定点\(A(6，0)\)，
则其中点\(Q(2cos\theta+3，1+2sin\theta)\)，
即点\(Q\)的参数方程为\(\begin{cases}x=2cos\theta+3\\y=1+2sin\theta\end{cases}(\theta为参数)\)，
消去参数得到，点\(Q\)的轨迹\(C_2\)的直角坐标方程为\((x-3)^2+(y-1)^2=4\)；
(2)、遇到直线和圆的位置关系问题，我们常常想到弦长半径和弦心距的\(Rt\Delta\)；
由题可知，直线\(l\)的直角坐标方程为\(y=ax\)，由\(|AB|\ge 2\sqrt{3}\)，
可得圆心\((3，1)\)到直线\(y=ax\)的点线距\(d=\sqrt{2^2-(\cfrac{2\sqrt{3}}{2})^2}\leq 1\)，
即\(d=\cfrac{|3a-1|}{a^2+1}\leq 1\)，平方得到
\((3a-1)^2\leq (a^2+1)\)，解得\(0\leq a\leq \cfrac{3}{4}\)；
故实数\(a\)的取值范围为\([0， \cfrac{3}{4}]\)；
\(\fbox{例9-2}\)(求轨迹方程)
已知圆\(C：x^2+y^2=4\)，直线\(l：x+y=2\)，以坐标原点为极点，\(x\)轴正半轴为极轴建立极坐标系，
(1)、将圆\(C\)和直线\(l\)的方程化为极坐标方程；
简析：\(C：\rho=2\)；\(l：\rho(cos\theta+sin\theta)=2\)
(2)、点\(P\)是直线\(l\)上的点，射线\(OP\)交圆\(C\)于点\(R\)，又点\(Q\)在\(OP\)上
且满足\(|OQ|\cdot|OP|=|OR|^2\)，当点\(P\)在直线\(l\)上移动时，求点\(Q\)的轨迹的极坐标方程；
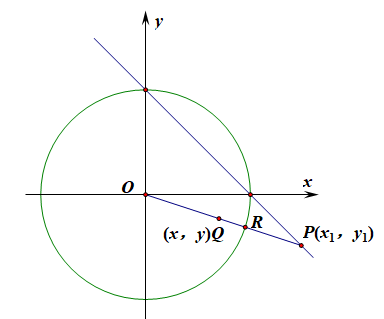
【思路一】：碰到这样的问题，我们一般是想着在直角坐标系下进行相应的运算，然后将结果转化成极坐标系即可，
设点\(P(x_1，y_1)\)，点\(Q(x，y)\)，
这样由\(|OQ|\cdot|OP|=|OR|^2\)，\(|OR|=2\)，变形得到\(\sqrt{x^2+y^2}\cdot \sqrt{x_1^2+y_1^2}=4①\)，
为得到关于点\(Q\)的轨迹方程，需要转化去掉方程中的变量\(x_1\)和\(y_1\)，
为此我们注意到\(\cfrac{x_1}{x}=\cfrac{y_1}{y}=t>0\)，则
\(x_1=t\cdot x\)，\(y_1=t\cdot y\)，
代入方程①得到，\(\sqrt{x^2+y^2}\cdot \sqrt{t^2x^2+t^2y^2}=4\)，
即\((x^2+y^2)\sqrt{t^2}=(x^2+y^2)\cdot t=4②\)
这样就多出来了一个变量\(t\)，只要将他想办法去掉就可以了，
又由于\(x_1+y_1=2\)，即\(tx+ty=2\)，
这样\(t=\cfrac{2}{x+y}\)，
代入方程②得到，\((x^2+y^2)\cdot\cfrac{2}{x+y}=4\)；
即点\(Q\)的轨迹方程的直角坐标方程为\(x^2+y^2=2(x+y)\)，
即点\(Q\)的轨迹方程为\(\rho=2(sin\theta+cos\theta)\)。
【思路二】：极坐标系法，设点\(P(\rho_1，\theta)\)，点\(Q(\rho，\theta)\)，点\(R(\rho_0，\theta)\)，
则有\(\rho_0=2\)，且\(\rho_1(cos\theta+sin\theta)=2\)，
则由\(|OQ|\cdot|OP|=|OR|^2\)，\(|OR|=2\)，得到\(\rho\cdot \rho_1=4\)，
即\(\rho\cdot \cfrac{2}{cos\theta+sin\theta}=4\)，
整理得到，\(\rho=2(sin\theta+cos\theta)\)，
即点\(Q\)的轨迹方程为\(\rho=2(sin\theta+cos\theta)\)。
解后反思：
1、通过两种思路的比较，我们基本能体会到极坐标系是有其自身的优越性的，
法1一开始是四个变量，法2一开始就只有三个变量\(\rho，\rho_1，\theta\)，
当将\(\rho_1\)做代换之后，立马就变成了两个变量，结果也就出来了。
2、由此题目我们还可以延伸思考，若给定条件是\(\cfrac{|OQ|}{|OP|}=4\)，或者\(|OQ|\pm|OP|=4\)，
那么用极坐标法都是比较简单的。
\(\fbox{例7}\)(伸缩变换)(2016洛阳模拟)
已知曲线\(C\)的极坐标方程是\(\rho=2\)，以极点为原点，极轴为\(x\)轴的正半轴建立平面直角坐标系，直线\(l\)的参数方程为
\(\begin{cases}x=1+t\\y=2+\sqrt{3}t\end{cases}(t为参数)\)，
（1）写出直线\(l\)的普通方程与曲线\(C\)的直角坐标方程；
（2）设曲线\(C\)经过伸缩变换\(\begin{cases}x'=x\\y'=\cfrac{1}{2}y\end{cases}\)得到曲线\(C'\)，设\(M(x，y)\)为曲线\(C'\)上任意一点，求\(x^2-\sqrt{3}xy+2y^2\)的最小值，并求相应的点\(M\)的坐标。
分析：(1)消去参数\(t\)，得到直线\(l\)的普通方程为\(\sqrt{3}x-y-\sqrt{3}+2=0\)
由\(\rho=2\)，得到曲线\(C\)的直角坐标方程为\(x^2+y^2=4\)；
(2)曲线\(C：x^2+y^2=4\)经过伸缩变换\(\begin{cases}x'=x\\y'=\cfrac{1}{2}y\end{cases}\)得到曲线\(C'\)，
即将\(x=x'，y=2y'\)代入\(C：x^2+y^2=4\)得到，\(x'^2+4y'^2=4\)，
整理得到曲线\(C'：\cfrac{x^2}{4}+y^2=1\)。
由曲线\(C'\)的参数方程得到点\(M(2cos\theta，sin\theta)\)，
即\(x=2cos\theta，y=sin\theta\)，代入得到
\(x^2-\sqrt{3}xy+2y^2=(2cos\theta)^2-\sqrt{3}\cdot 2cos\theta\cdot sin\theta+2sin^2\theta\)
\(=4cos^2\theta+2sin^2\theta-\cfrac{\sqrt{3}}{2}sin2\theta\)
\(=2+2cos^2\theta-\cfrac{\sqrt{3}}{2}sin2\theta\)
\(=2+1+cos2\theta-\cfrac{\sqrt{3}}{2}sin2\theta\)
\(=3-2sin(2\theta-\cfrac{\pi}{6})\)
当\(2\theta-\cfrac{\pi}{6}=2k\pi+\cfrac{\pi}{2}(k\in Z)\)，
即\(\theta=k\pi+\cfrac{\pi}{3}(k\in Z)\)时，
即点\(M(1，\cfrac{\sqrt{3}}{2})\)或\(M(-1，-\cfrac{\sqrt{3}}{2})\)时，
\(x^2-\sqrt{3}xy+2y^2\)的最小值为1.
\(\fbox{例8}\)【2019届凤中高三理科月考1第22题】
在平面直角坐标系\(xoy\)中，直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=2+t}\\{y=1+2t}\end{array}\right.(t为参数)\)，以原点为极点，以\(x\)轴的非负半轴为极轴建立极坐标系，\(\odot C\)的极坐标方程为\(\rho^2-4\rho sin\theta-12=0\)，
(1) 求\(\odot C\)的参数方程；
分析：将\(\rho^2=x^2+y^2\)，\(y=\rho\cdot sin\theta\)
代入\(\odot C\)的极坐标方程\(\rho^2-4\rho sin\theta-12=0\)，
得到\(\odot C\)的直角坐标方程为\(x^2+y^2-4y-12=0\)，
即\(x^2+(y-2)^2=16=4^2\)，
故\(\odot C\)的参数方程为\(\left\{\begin{array}{l}{x=4cos\theta}\\{y=2+4sin\theta}\end{array}\right.\) \((\theta为参数，\theta\in [0，2\pi))\)。
(2)求直线\(l\)被\(\odot C\)截得的弦长。
【法1，几何方法，\(Rt\Delta\)】将直线\(l\)的参数方程消参，得到其普通方程为\(2x-y-3=0\)，
则圆心\((0，2)\)到直线的距离为\(d=\cfrac{|-2-3|}{\sqrt{2^2+1^2}}=\sqrt{5}\)，
则直线\(l\)被\(\odot C\)截得的弦长为\(2\sqrt{r^2-d^2}=2\sqrt{4^2-(\sqrt{5})^2}=2\sqrt{11}\)。
【法2，弦长公式】设直线和圆的交点为\(A(x_1，y_1)，B(x_2，y_2)\)，
联立得到方程组，\(\left\{\begin{array}{l}{2x-y-3=0}\\{x^2+y^2-4y-12=0}\end{array}\right.\)
消去\(y\)得到，\(x^2+(2x-3)^2-4(2x-3)-12=0\)，
整理得到，\(5x^2-20x+9=0\)，
由韦达定理得到，\(x_1+x_2=4\)，\(x_1x_2=\cfrac{9}{5}\)，
由弦长公式得到，\(|AB|=\sqrt{1+k^2}|x_1-x_2|\)
\(=\sqrt{1+2^2}\sqrt{(x_1+x_2)^2-4x_1x_2}\)
\(=\sqrt{5}\sqrt{16-\cfrac{36}{5}}=2\sqrt{11}\)。
【法3，利用直线的参数方程求解】图像解释
直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=2+t}\\{y=1+2t}\end{array}\right.(t为参数)\)，
(此时千万要注意，弦长\(|AB|\neq |t_1-t_2|\)，原因是这个参数方程不是标准形式的)
将其做如下的转化，
\(\left\{\begin{array}{l}{x=2+\cfrac{1}{\sqrt{5}}\cdot \sqrt{5}t}\\{y=1+\cfrac{2}{\sqrt{5}}\cdot \sqrt{5}t}\end{array}\right.(t为参数)\)，
令\(\sqrt{5}t=m\)，则其参数方程的标准形式为
\(\left\{\begin{array}{l}{x=2+\cfrac{1}{\sqrt{5}}\cdot m}\\{y=1+\cfrac{2}{\sqrt{5}}\cdot m}\end{array}\right.(m为参数)\)，
【此时参数\(m\)的几何意义才是动点到静点的距离的数量，千万要注意，即弦长\(|AB|=|m_1-m_2|\)】
将直线\(l\)的参数方程的标准形式代入圆的普通方程得到，
\((2+\cfrac{1}{\sqrt{5}}m)^2+(1+\cfrac{2}{\sqrt{5}}m)^2-4(1+\cfrac{2}{\sqrt{5}}m)-12=0\)
整理为\(m^2-11=0\)，
令直线和圆的两个交点\(A，B\)分别对应的参数为\(m_1，m_2\)，
则\(m_1+m_2=0\)，\(m_1m_2=-11\)，
此时弦长\(|AB|=|m_1-m_2|=\sqrt{(m_1+m_2)^2-4m_1m_2}=\sqrt{4\times 11}=2\sqrt{11}\)。