理论分布和抽样分布------（四）抽样分布

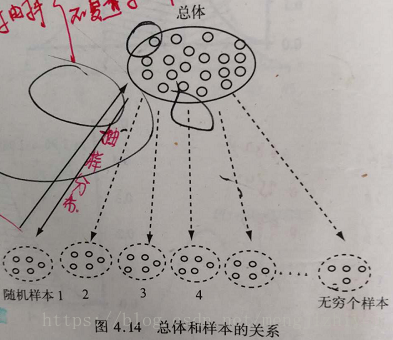
统计学的一个主要任务就是研究总体和样本之间的关系。这种关系可以从两个方向进行：

（1）从总体到样本的方向，目的是要研究从总体中抽出的所有可能样本统计量的分布及其与原总体的关系，即抽样分布

（2）从样本到总体的方向，从总体中随机抽取样本，并用样本对总体作出推论，即统计推断问题。

抽样分布（sampling distribution）是统计推断的基础。

一、统计数的抽样及其分布参数

从总体中随机抽样得到样本，获得样本观察值后计算一些统计数，统计数分布称为抽样分布。

抽样分为复置抽样（将抽得的个体放回总体后再继续抽样）和不复置抽样（将抽得的个体不放回总体而继续抽样）。

（1）样本平均数的抽样及其分布参数

一个总体进行随机抽样可得到许多样本，如果总体是无限总体，那么可以得到无限多个随机样本。如果从容量为N的有限总体抽样，若每次抽取容量为n的样本，那么一共可以得到 $N^n$ 个样本（所有可能的样本个数）。

抽样所得到的每一个样本可以计算一个平均数，全部可能的样本都被抽取后可得到许多平均数，如 $\bar{y}_1,\bar{y}_2,\bar{y}_3,...,\bar{y}_m$ 等。m代表抽样所可能得到的所有平均数的总个数。如果被抽样的总体是无限总体，m代表无穷大的正整数，有限总体m= $N^n$ 。

将抽样所得到的所有可能的样本平均数集合起来构成一个新的总体，该总体是由原总体或母总体抽样得到的，它的变数资料是由所有样本平均数构成的，平均数 $\bar{y}$ 就成为一个新总体的变量。每一次随机抽样所得到的平均数会有差异，所有由平均数构成的新总体也应有其分布，这种分布称为平均数的抽样分布。

随机样本的任何一种统计数都可是一个变量，这种变量的分布称为统计数的抽样分布。

新总体是由母总体中通过随机抽样得到的，新总体与母总体必然有关系。数理统计的推导表明新总体与母总体在特征参数上存在函数关系。平均数抽样分布为例：

（1）该抽样分布的平均数 $\mu_{\bar{y}}$ （所有样本平均数的平均数）与母总体的平均数相等： $\mu_{\bar{y}}=\mu$

（2）该抽样分布的方差 $\sigma _{\bar{y}}^2$ （所有样本平均数间的方差）与母总体方差 $\sigma ^2$ 间存在如下关系： $\sigma _{\bar{y}}^2=\sigma ^{2}/n$

n：样本容量抽样分布的标准差又称标准误，可度量抽样分布的变异。

二、样本总和数的抽样及其分布参数

样本总和数 $\sum y$ 的抽样分布参数与母总体间关系：

（1）抽样分布的平均数 $\mu_{\sum y}$ 与母总体平均数： $\mu_{\sum y}=n\mu$

（2）抽样分布的方差 $\sigma _{\sum{y}}^2$ 与母总体方差： $\sigma _{\sum{y}}^2=n\sigma ^2$

三、两个独立随机样本平均数差数的抽样及其分布参数

从一个总体随机抽取一个样本为 $n_1$ 的样本，同时随机独立地从另一个总体抽取一个样本容量为 $n_2$ 的样本，那么可得到分别属于两个总体的样本，两样本的平均数分别用 $\bar{y}_1$ 和 $\bar{y}_{2}$ 。设这两个样本所来自的两个总体的平均数分别为 $\mu _1$ 和 $\mu _{2}$ ，方差分别为 $\sigma _1^2$ , $\sigma _2^2$ .

根据数理统计的推导，两个独立随机抽取的样本平均数间差数（ $\bar{y}_1$ - $\bar{y}_{2}$ ）的抽样分布参数与两个母总体间关系：

（1）该抽样分布的平均数 $\mu_{\bar{y}_1-\bar{y}_2}$ 与母总体平均数之差相等： $\mu_{\bar{y}_1-\bar{y}_2}$ = $\mu _1$ - $\mu _{2}$

（2）抽样分布的方差 $\sigma _{\bar{y}_1-\bar{y}_2}^2$ 与母总体方差间关系： $\sigma _{\bar{y}_1-\bar{y}_2}^2=\sigma _{\bar{y}_1}^2+\sigma _{\bar{y}_2}^2=\frac{\sigma _1^2}{n_1}+\frac{\sigma _2^2}{n_2}$

四、正态总体抽样的分布规律

（1）样本平均数的分布

从正态总体抽取的样本，无论样本容量大或小，其样本平均数 $\bar{y}$ 的抽样分布比做成正态分布，具有平均数 $\mu_{\bar{y}}=\mu$ ,方差 $\sigma _{\bar{y}}^2=\sigma ^{2}/n$ ，方差随样本容量增大而递降。平均数的分布记为 $N(\mu_{\bar{y}},\sigma ^{2}/n)$ 。随样本容量的增加，分布的集中程度增加了，说明方差减少了。

若母总体不是正态分布从中抽出 $\bar{y}$ 的分布不一定属于正态分布，但当样本容量n增大时，从这总体抽出样本平均数 $\bar{y}$ 的抽样分布，趋近于正态分布，具平均数 $\mu$ 和方差 $\sigma ^{2}/n$ ，这是中心极限定理决定的。

中心极限定理说明只要样本容量适当大，不论总体分布形状如何，其 $\bar{y}$ 的分布都可看做正态分布。实际应用时，n>30就可应用这一定理。

（2）两个独立样本平均数差数的分布

假定有两个正态总体各具有平均数和标准差 $\mu _1$ ， $\sigma _1$ 和 $\mu _{2}$ , $\sigma _2$ ,从第一个总体随机抽取 $n_1$ 观察值，从第二个总体随机抽取 $n_2$ 观察值。计算出样本平均数和标准差 $\bar{y}_1$ ， $s_1$ 和 $\bar{y}_{2}$ ， $s_2$ 。

从统计理论可推导出其样本平均数的差数（ $\bar{y}_1$ - $\bar{y}_{2}$ ）的抽样分布，具以下特性：

（1）如果两个总体各作正态分布，则其样本平均数差数遵循正态分布律，无论样本容量大或小，都有N（ $\mu_{\bar{y}_1-\bar{y}_2}$ ， $\sigma _{\bar{y}_1-\bar{y}_2}^2$ ）。

（2）两个样本平均数差数分布的平均数必等于两个总体平均数的差数

（3）两个独立的样本平均数差数分布的方差等于两个总体的样本平均数的方差总和

（4）若两个样本抽自于同一正态总体，其平均数差数的抽样分布不论容量大小亦作正态分布 $\mu_{\bar{y}_1-\bar{y}_2}$ =0

（5）若两个样本抽自于同一总体，但非正态总体，其平均数差数的分布按中心极限定理在 $n_1$ ， $n_2$ 相当大时（n>30）才逐渐接近于正态分布。

（6）若两个样本抽自于两个非正态总体， $\sigma _1^2$ ， $\sigma _2^2$ 相差很大时，则其平均数差数的抽样分布很难确定。 $\sigma _1^2$ ， $\sigma _2^2$ 相差不太远时，也可近似地应用正态接近方法估计平均数差数出现的次数，这种估计的可靠性得依两总体偏离正态的程度和相差大小而转移。