
解法一:我们先用最朴素的方法,着眼于每个物体是否进入背包,进行遍历。
代码如下:
#include<iostream> #include<algorithm> using namespace std; int N,W; const int maxn=105; int v[maxn],w[maxn]; int rec(int i,int j){//从第i个下标开始,计算剩余j重量怎么挑选商品 int ans; if(i==N) ans=0;//已经没有商品可以选择 else if(j<w[i]) ans=rec(i+1,j);//如果背包容量装不下下标为i的商品 else ans=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]); return ans; } int main(){ cin>>N>>W; for(int i=0;i<N;i++) cin>>w[i]; for(int i=0;i<N;i++) cin>>v[i]; int res=rec(0,W); cout<<res<<endl; return 0; }
然而这种算法是对每个商品都进行处理,每一层搜索都有两个分支,时间复杂度为O(2^n),当n比较大的时候就会花费较多的时间。我们注意到,对每个商品进行搜索的时候,有时会出现相同的参数,
于是第二次调用的时候我们其实已经计算过一次了,等于是白白浪费了时间。所以我们有了新的想法:把第一次计算的结果给记录下来,这样可以省下不少时间。
于是有了解法二:
用一个二维数组记录下之前第一次计算出的结果,等到第二次调用相同参数函数的时候,就不必计算。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 const int maxN=3405; 6 const int maxW=405; 7 int dp[maxN][maxW]; 8 int N,W; 9 int w[maxW],v[maxN]; 10 int rec(int i,int j){ 11 if(dp[i][j]>=0) return dp[i][j]; 12 int ans; 13 if(i==N) ans=0; 14 else if(j<w[i]) ans=rec(i+1,j); 15 else ans=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]); 16 return dp[i][j]=ans; 17 } 18 int main(){ 19 memset(dp,-1,sizeof(dp)); 20 cin>>N>>W; 21 for(int i=0;i<N;i++) 22 { 23 cin>>w[i]; 24 cin>>v[i]; 25 } 26 int res=rec(0,W); 27 cout<<res<<endl; 28 return 0; 29 } 30
观察这个记忆化数组,我们如果把dp[i][j]定义成如下意义:当总重量小于j时,从下标为i的商品开始挑选,得到商品的最大值。于是有下面的递推公式:
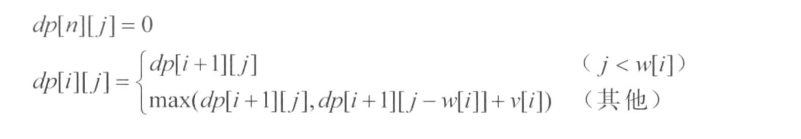
这就相当于一个逆向递推,我们可以利用一个二重循环,利用递推公式将每一项的值算出来。

如同这张表格所示,我们是从下标i=3开始计算(这里需要把dp二维数组的初始值全化为0,在下面的代码中,由于定义的是全局数组,对于只有一个输入样例的情况下主函数中不必再次初始化,
如果问题有多组输入,则主函数需要初始化dp数组)。可以自己动手画一张表格,自己算一算每格的值。这样很有利于理解下面的代码。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 const int maxN=3405; 6 const int maxW=405; 7 int dp[maxN][maxW]; 8 int N,W; 9 int w[maxW],v[maxN]; 10 void solve(){ 11 for(int i=N-1;i>=0;i--){ 12 for(int j=0;j<=W;j++){ 13 if(j<w[i]) 14 dp[i][j]=dp[i+1][j]; 15 else 16 dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]); 17 } 18 } 19 20 cout<<dp[0][W]<<endl; 21 } 22 int main(){ 23 cin>>N>>W; 24 for(int i=0;i<N;i++) 25 { 26 cin>>w[i]; 27 cin>>v[i]; 28 } 29 solve(); 30 return 0; 31 } 32
这就是解法三。
当然,有了逆向递推,我们自然也会想到正向递推,只不过需要将dp[i][j]的意义重新定义一下。
如果我们将dp[i+1][j]意义定义为:从前i个商品中挑选重量不超过j的的物品时,价值的最大值。(这里的i是指下标,是从0开始的),就会有下面的递推公式和表格:
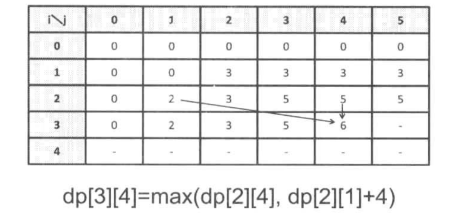
代码如下:
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 const int maxN=3405; 6 const int maxW=405; 7 int dp[maxN][maxW]; 8 int N,W; 9 int w[maxW],v[maxN]; 10 void solve(){ 11 for(int i=0;i<N;i++){ 12 for(int j=0;j<=W;j++){ 13 if(j<w[i]) 14 dp[i+1][j]=dp[i][j]; 15 else 16 dp[i+1][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]); 17 } 18 } 19 20 cout<<dp[N][W]<<endl; 21 } 22 int main(){ 23 cin>>N>>W; 24 for(int i=0;i<N;i++) 25 { 26 cin>>w[i]; 27 cin>>v[i]; 28 } 29 solve(); 30 return 0; 31 } 32