一、简介
牛顿方法同梯度下降法一样,是一种优化算法,其应用如可解决logistic回归于分类问题中的似然函数最大化。
其是一种用于求函数零点的数值方法。
二、具体形式
首先选择一个与零点相近的起始点,之后遵循以下更新规则不断更新:
实际上,对于f(x)上的一个点(x0,f(x0)),求过此点切线(即斜率为f'(x0))与x轴的交点,即解以下方程

若原先的点x0记作xn,新得到的点x记为xn+1,那么解得
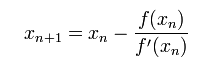
这便是update rule的来源。
三、其它理解
已经证明,如果f ' 是连续的,并且待求的零点x是孤立的,那么在零点x周围存在一个区域,只要初始值x0位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果f ' (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。
由于牛顿法是基于当前位置的切线来确定下一次的位置,所以牛顿法又被很形象地称为是"切线法"。牛顿法的搜索路径(二维情况)如下图所示:
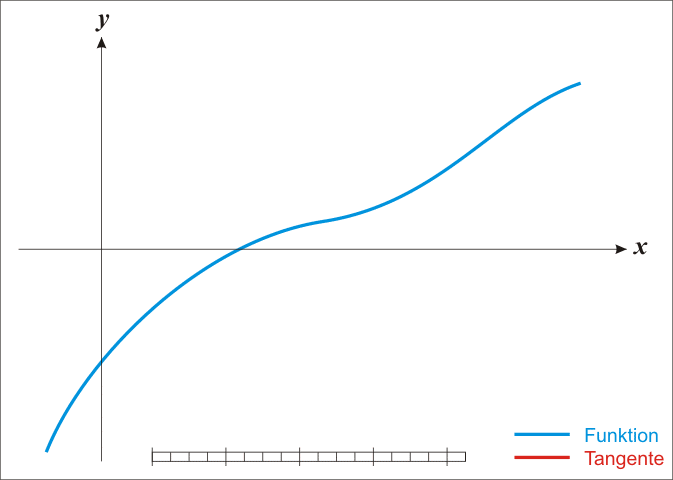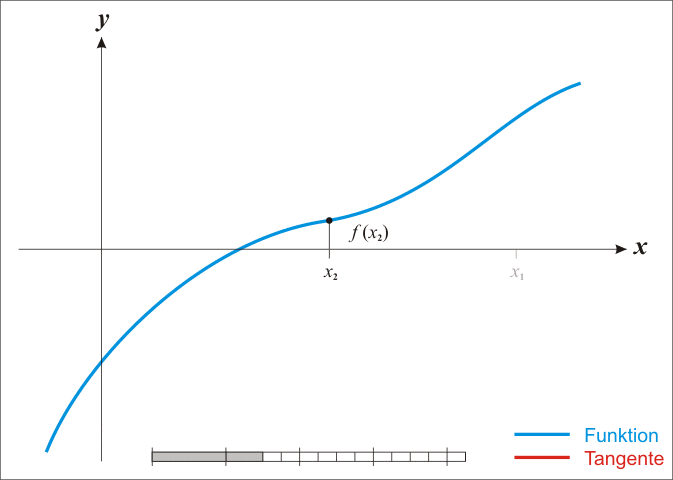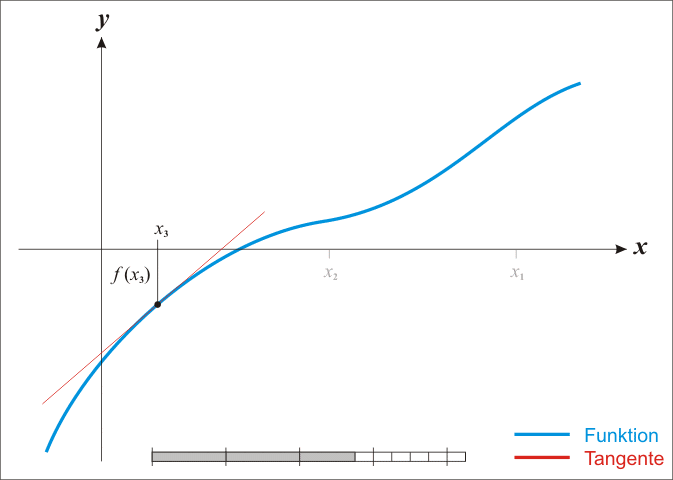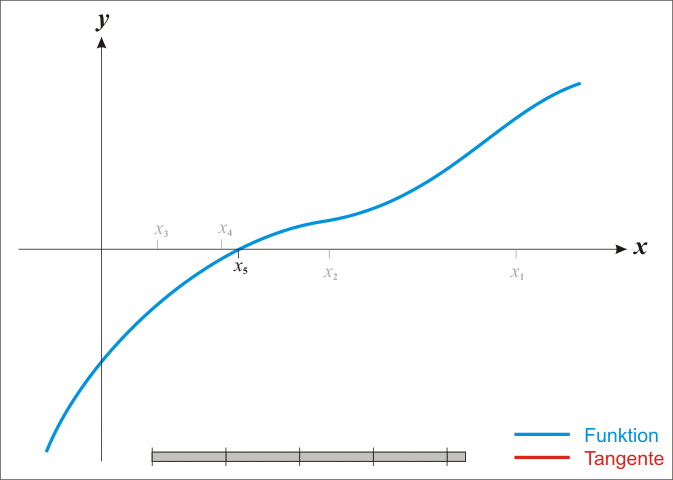
从本质上去看,牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法就更快。如果更通俗地说的话,比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。(牛顿法目光更加长远,所以少走弯路;相对而言,梯度下降法只考虑了局部的最优,没有全局思想。)
根据wiki上的解释,从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
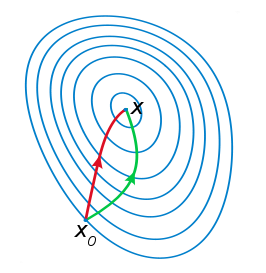
注:红色的牛顿法的迭代路径,绿色的是梯度下降法的迭代路径。
牛顿法的优缺点总结:
优点:二阶收敛,收敛速度快;
缺点:牛顿法是一种迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
来源:https://www.cnblogs.com/shixiangwan/p/7532830.html
四、优化的应用
如何找到我们最开始说的似然函数l(θ)的最大值呢?很显然,找到其最大值等同于找到l'(θ)=0的零点,即遵循以下方法得到参数最大值:
五、牛顿法的矩阵表示
如下
其中▽θ表示对矩阵每个元素求偏导数,H为Hessian矩阵,其矩阵元素为



