电磁学乱七八糟的符号(四)

@(study)[Maxe, markdown_study, LaTex_study]

author:何伟宝

这里重点是一般传输规律和矩形波导,chapter6 电磁波的传输

电磁学乱七八糟的符号(四)

纵向场量法

说白了也就是从麦克斯韦方程式抽象出我们需要的波动方程,流程如下:
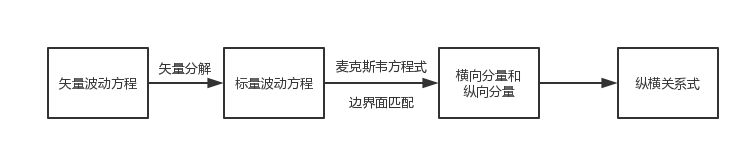
peocess

矢量波动方程

在无源自由空间场量中(由麦克斯韦方程式):

\begin{matrix} (1.1) & \nabla^{2} \vec{E} + k^{2} \vec{E} = 0 \end{matrix}

$\nabla^2 \vec E+k^2\vec E=0 \tag{1.1}$

\begin{matrix} (1.2) & \nabla^{2} \vec{H} + k^{2} \vec{H} = 0 \end{matrix}

$\nabla^2 \vec H+k^2\vec H=0 \tag{1.2}$
在波导中,设电磁波沿着z轴传输:

\begin{matrix} (1.3) & \vec{E} (x, y, z) = \vec{E} (x, y) e^{γ r} \end{matrix}

$\vec E(x,y,z) = \vec E(x,y)e^{\gamma r } \tag{1.3}$

\begin{matrix} (1.4) & \vec{H} (x, y, z) = \vec{H} (x, y) e^{γ r} \end{matrix}

$\vec H(x,y,z) = \vec H(x,y)e^{\gamma r } \tag{1.4}$
其中有:

行波因子 $\gamma$

在上一章说过他也是一个传播常数,当 $\gamma$ 为实数时,信号衰减.虚数时信号传播,且波数为其虚部

矢量分解

这里有意地把纵横量分开了:

\vec{E} = ({\vec{a}}_{x} E_{x} + {\vec{a}}_{y} E_{y}) + {\vec{a}}_{z} E_{z}

$\vec E = (\vec a_x E_x+\vec a_y E_y) + \vec a_z E_z$

\vec{H} = ({\vec{a}}_{x} H_{x} + {\vec{a}}_{y} H_{y}) + {\vec{a}}_{z} H_{z}

$\vec H = (\vec a_x H_x+\vec a_y H_y) + \vec a_z H_z$
顺便把拉普拉斯算符

\nabla

$\nabla$ 也分开:

\nabla_{t}^{2} = (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) + \frac{\partial^{2}}{\partial z^{2}} = \nabla_{x y}^{2} + \frac{\partial^{2}}{\partial z^{2}}

$\nabla_t^2 = (\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2})+ \frac {\partial^2}{\partial z^2}=\nabla^2_{xy}+\frac {\partial^2}{\partial z^2}$

标量波动方程

将矢量分解的三个方程先带入(1.3)(1.4)再代入(1.1)(1.2),只截取纵向分量得:

\nabla_{x y}^{2} {\vec{E}}_{z} + (k^{2} + γ^{2}) {\vec{E}}_{z} = 0

$\nabla^2_{xy}\vec E_z+(k^2+\gamma^2)\vec E_z=0$

\nabla_{x y}^{2} {\vec{H}}_{z} + (k^{2} + γ^{2}) {\vec{H}}_{z} = 0

$\nabla^2_{xy}\vec H_z+(k^2+\gamma^2)\vec H_z=0$

再将上式改写成(1.3)(1.4)形式:

E_{z} (x, y, z) = E_{z} (x, y) E^{- γ z}

$E_z(x,y,z) = E_z(x,y)E^{-\gamma z}$

H_{z} (x, y, z) = H_{z} (x, y) H^{- γ z}

$H_z(x,y,z) = H_z(x,y)H^{-\gamma z}$

考虑麦克斯韦方程的旋度式:

\nabla \times \vec{E} = - j ω μ \vec{H}

$\nabla \times \vec E=-j\omega \mu \vec H$

\nabla \times \vec{H} = j ω ε \vec{E}

$\nabla\times\vec H =j\omega\varepsilon \vec E$
联立上四式可得六个标量方程:

\begin{matrix} (标量1) & \frac{\partial E_{z}}{\partial y} + γ E_{y} = - j ω μ H_{x} \end{matrix}

$\frac{\partial E_z}{\partial y}+\gamma E_y = -j\omega \mu H_x \tag{标量1}$

\begin{matrix} (标量2) & - γ E_{x} - \frac{\partial E_{z}}{\partial x} = - j ω μ H_{y} \end{matrix}

$-\gamma E_x -\frac{\partial E_z}{\partial x}=-j\omega \mu H_y \tag{标量2}$

\begin{matrix} (标量3) & \frac{\partial E_{y}}{\partial x} - \frac{\partial E_{x}}{\partial x} = - j ω μ H_{z} \end{matrix}

$\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial x}=-j\omega \mu H_z \tag{标量3}$
千万不要慌,由麦克斯韦美好的对称性可以知道,我们只要算一对叉乘就可以了,由对称性:

\begin{matrix} (标量4) & \frac{\partial H_{z}}{\partial y} + γ H_{y} = j ω ε E_{x} \end{matrix}

$\frac{\partial H_z}{\partial y}+\gamma H_y = j\omega \varepsilon E_x \tag{标量4}$

\begin{matrix} (标量5) & - γ H_{x} - \frac{\partial H_{z}}{\partial x} = j ω ε E_{y} \end{matrix}

$-\gamma H_x -\frac{\partial H_z}{\partial x}=j\omega \varepsilon E_y \tag{标量5}$

\begin{matrix} (标量6) & \frac{\partial H_{y}}{\partial x} - \frac{\partial H_{x}}{\partial x} = j ω ε E_{z} \end{matrix}

$\frac{\partial H_y}{\partial x}-\frac{\partial H_x}{\partial x}=j\omega \varepsilon E_z \tag{标量6}$

纵横关系式

联立以上六式可得(解这个会有点痛苦,但是这不重要)纵横关系式:

\begin{matrix} (e.x) & E_{x} = - \frac{1}{k_{c}^{2}} (γ \frac{\partial E_{z}}{\partial x} + j ω μ \frac{\partial H_{z}}{\partial y}) \end{matrix}

$E_x = -\frac {1} {k_c^2}(\gamma\frac{\partial E_z}{\partial x}+j\omega\mu\frac{\partial H_z}{\partial y})\tag{e.x}$

\begin{matrix} (e.y) & E_{y} = - \frac{1}{k_{c}^{2}} (γ \frac{\partial E_{z}}{\partial y} - j ω μ \frac{\partial H_{z}}{\partial x}) \end{matrix}

$E_y = -\frac {1} {k_c^2}(\gamma\frac{\partial E_z}{\partial y}-j\omega\mu\frac{\partial H_z}{\partial x})\tag{e.y}$

\begin{matrix} (h.x) & H_{x} = - \frac{1}{k_{c}^{2}} (γ \frac{\partial H_{z}}{\partial x} - j ω μ \frac{\partial E_{z}}{\partial y}) \end{matrix}

$H_x = -\frac {1} {k_c^2}(\gamma\frac{\partial H_z}{\partial x}-j\omega\mu\frac{\partial E_z}{\partial y})\tag{h.x}$

\begin{matrix} (h.y) & E_{x} = - \frac{1}{k_{c}^{2}} (γ \frac{\partial H_{z}}{\partial x} + j ω μ \frac{\partial E_{z}}{\partial x}) \end{matrix}

$E_x = -\frac {1} {k_c^2}(\gamma\frac{\partial H_z}{\partial x}+j\omega\mu\frac{\partial E_z}{\partial x})\tag{h.y}$
其中:

k_{c}^{2} = k^{2} + γ^{2}

$k_c^2=k^2+\gamma^2$
如果不用书本的表示方法的话,你会发现一点公式的美学…

自此,纵向常量法就介绍完成了.这里的重点在于纵横关系式

各种导波的一般传输特性

概述

这一小节解决的问题是,某种电磁波要在波导中传输的存在可能性问题.重点有TEM,TE,TM波等.并且提供假设各种波存在的时候,怎么求解波动方程的思路.

TEM横电磁波

还是回到我们熟悉的波动方程,可以把上面的纵横关系式:

\begin{matrix} (波动1) & \nabla_{x y}^{2} E_{z} + k_{c}^{2} E_{z} = 0 \end{matrix}

$\nabla^2_{xy}E_z + k_c^2 E_z=0 \tag{波动1}$

\begin{matrix} (波动2) & \nabla_{x y}^{2} H_{z} + k_{c}^{2} H_{z} = 0 \end{matrix}

$\nabla^2_{xy}H_z + k_c^2 H_z=0 \tag{波动2}$
显然这一节的教材安排是不合理的…因为在TEM波中:

E_{z} = 0, H_{z} = 0

$E_z=0,H_z=0$
显然代入纵横关系式中,全军覆没……所以分析横电磁波的时候不能采用纵向常量法得到直接表达式
这时候我们可以代入得到纵横关系式前面一点的关系式中:

\begin{matrix} (2.1) & k_{c}^{2} = 0 或 γ^{2} + k^{2} = 0 \end{matrix}

$k_c^2=0\quad或\quad\gamma^2+k^2=0\tag{2.1}$

\begin{matrix} (tem) & \nabla_{x y}^{2} \vec{E} (x, y) = 0 \nabla_{x y}^{2} \vec{H} (x, y) = 0 \end{matrix}

$\nabla^2_{xy}\vec E(x,y)=0 \quad \quad \nabla^2_{xy}\vec H(x,y)=0 \tag{tem}$
那么我们就可以知道,代入纵横关系式会凉凉的原因是,(tem)他看上去就是一个静态场的方程,用麦克斯韦旋度式便变成0了.

这也启发我们,在求解TEM波动方程的时候,之需要先算出导波的横向分布函数,再乘以纵向传播因子 $e^{-\gamma z}$ 就可以得到波动方程了.而且并不是每一种波导都会有TEM模.

存在条件

首先说明的一点是:空心波导只能传输TM或TE波,不能传输TEM波,因为在无外源的无限长导体空管中不可能存在静电场
书上P175,结合来看吧..(懒得打字)

TEM传播常数和相速

由(2.1)可知

γ = α + j β = j k = j ω \sqrt{ε μ}

$\gamma=\alpha+j\beta =jk=j\omega \sqrt{\varepsilon \mu}$
解得

α = 0, β = ω \sqrt{ε μ}

$\alpha =0 \quad,\quad \beta =\omega\sqrt{\varepsilon \mu}$
所以相速为:

v = \frac{ω}{β} = \frac{1}{\sqrt{ε μ}}

$v=\frac {\omega}{\beta}=\frac1{\sqrt{\varepsilon \mu}}$
可以看出TEM模导行波是与频率无关的非色散波

TEM的波阻抗

由(标量2)和(标量6)并代入TEM的定义式:

γ E_{x} = j ω μ H_{y}

$\gamma E_x=j\omega \mu H_y$

γ H_{y} = j ω ε E_{x}

$\gamma H_y=j\omega \varepsilon E_x$
代入

γ = j ω \sqrt{ε μ}

$\gamma = j\omega\sqrt{\varepsilon \mu}$ 得(注意,求解不是联立.只要用其中一条代入就行了)

Z^{T E M} = \frac{E_{x}}{H_{y}} = \sqrt{\frac{μ}{ε}} = η

$Z^{TEM}=\frac{E_x}{H_y}=\sqrt{\frac{\mu}{\varepsilon}}=\eta$
可以看出,

Z^{T E M}

$Z^{TEM}$ 和频率是没有关系的.
所以: TEM模在任何频率下都能传播非色散横电磁波

TE nor TM

在TM波中, $E_z \neq 0$ 和 $H_z=0$ .所以只需要代入(波动1),同理:
在TE波中, $H_z \neq 0$ 和 $E_z=0$ .所以只需要代入(波动2)

存在条件

可以看出,无论是哪一种, $k_c^2$ 都不会等于0,所以:

γ^{2} + k^{2} \neq 0

$\gamma^2+k^2 \neq 0$
被称为波导中TM波和TE波的存在条件。

传播常数和截止频率

由传播因子 $e^{-j\gamma z}$ 可以知道，在 $e^{-\gamma z}\to 0$ 时,传播截止.这个时候有 $\gamma \to 1$
所以有:

γ = \sqrt{k_{c}^{2} - ω_{c}^{2} ε μ} = 0

$\gamma=\sqrt{k^2_c-\omega_c^2 \varepsilon \mu}=0$
解得:

f_{c} = \frac{k_{c}}{2 π \sqrt{ε μ}}

$f_c=\frac{k_c}{2\pi\sqrt{\varepsilon\mu}}$
其中,

f_{c}

$f_c$ 被称为 截止频率或临界频率(c to cut),所以反过来求

γ

$\gamma$ 得:

γ = {\begin{cases} j k \sqrt{1 - (\frac{f_{c}}{f})^{2}} = j β f > f_{c} \\ k_{c} \sqrt{1 - (\frac{f_{c}}{f})^{2}} = α f < f_{c} \end{cases}

$\gamma=\begin{cases} jk\sqrt{1-(\frac{f_c}{f})^2}= j\beta \quad f>f_c \\k_c\sqrt{1-(\frac{f_c}{f})^2}=\alpha\quad f<f_c \end{cases}$
可以看出:
当

f < f_{c}

$f<f_c$ 时,传播因子变成了

e^{- α z}

$e^{-\alpha z}$ ,是一个衰减型凋落场
当

f > f_{c}

$f>f_c$ 时,传播因子变成了

e^{- j β z}

$e^{-j\beta z}$ ,表示一个传播型色散行波

相速和波导波长

当 $f>f_c$ 时,因为是一个色散波,我们可以来讨论一下他的相速,由上面:

β = k \sqrt{1 - (\frac{f_{c}}{f})^{2}}

$\beta=k\sqrt{1-(\frac{f_c}{f})^2}$
所以有,相速:

v_{p} = \frac{ω}{β} = \frac{v}{\sqrt{1 - (\frac{f_{c}}{f})^{2}}} > v

$v_p=\frac\omega\beta=\frac{v}{\sqrt{1-(\frac{f_c}{f})^2}}>v$

波导内波导行波的波长称为波导波长:

λ_{g} = \frac{2 π}{β} = \frac{2 π}{k} \frac{1}{\sqrt{1 - (\frac{f_{c}}{f})^{2}}} = \frac{λ}{\sqrt{1 - (\frac{f_{c}}{f})^{2}}} > λ

$\lambda_g=\frac{2\pi}{\beta}=\frac{2\pi}{k}\frac1{\sqrt{1-(\frac{f_c}{f})^2}}=\frac\lambda{\sqrt{1-(\frac{f_c}{f})^2}} >\lambda$
表明导行波是与频率有关的色散行波

波阻抗

TM波

由纵横关系式,结合tm波的特征可得:

E_{x} = - \frac{γ}{k_{c}^{2}} ∙ \frac{\partial E_{z}}{\partial x}

$E_x=-\frac{\gamma}{k_c^2}\bullet\frac{\partial E_z}{\partial x}$

E_{y} = - \frac{γ}{k_{c}^{2}} ∙ \frac{\partial E_{z}}{\partial y}

$E_y=-\frac{\gamma}{k_c^2}\bullet\frac{\partial E_z}{\partial y}$

H_{x} = \frac{j ω ε}{k_{c}^{2}} ∙ \frac{\partial E_{z}}{\partial y}

$H_x=\frac{j\omega\varepsilon}{k_c^2}\bullet\frac{\partial E_z}{\partial y}$

E_{y} = - \frac{j ω ε}{k_{c}^{2}} ∙ \frac{\partial E_{z}}{\partial x}

$E_y=-\frac{j\omega\varepsilon}{k_c^2}\bullet\frac{\partial E_z}{\partial x}$
所以定义TM波的波阻抗为:

Z^{T M} = \frac{E_{x}}{H_{y}} = \frac{- E_{y}}{H_{x}} = \frac{γ}{j ω ε}

$Z^{TM}=\frac{E_x}{H_y}=\frac{-E_y}{H_x}=\frac{\gamma}{j\omega\varepsilon}$
消去

γ

$\gamma$ 得:

Z^{T M} = {\begin{cases} η \sqrt{1 - (\frac{f_{c}}{f})^{2}} = R^{T M}, f > f_{c} \\ - j \frac{k_{c}}{ω ε} \sqrt{1 - (\frac{f_{c}}{f})^{2}} = - j X_{c}^{T M}, f < f_{c} \end{cases}

$Z^{TM}=\begin{cases}\eta\sqrt{1-(\frac{f_c}{f})^2} =R^{TM},\quad \quad\quad\quad f>f_c \\-j\frac{k_c}{\omega\varepsilon}\sqrt{1-(\frac{f_c}{f})^2}=-jX_c^{TM}, \quad f<f_c \end{cases}$

TE波

按照TM波的套路,代入 $E_z=0$ 得:

Z^{T M} = {\begin{cases} η \frac{1}{\sqrt{1 - (\frac{f_{c}}{f})^{2}}} = R^{T E}, f > f_{c} \\ j \frac{μ ω}{k_{c}} \frac{1}{\sqrt{1 - (\frac{f_{c}}{f})^{2}}} = j X_{c}^{T E}, f < f_{c} \end{cases}

$Z^{TM}=\begin{cases}\eta\frac1{\sqrt{1-(\frac{f_c}{f})^2}} =R^{TE},\quad \quad\quad\quad f>f_c \\j\frac{\mu\omega}{k_c}\frac1{\sqrt{1-(\frac{f_c}{f})^2}}=jX_c^{TE},\quad \quad \quad f<f_c \end{cases}$

互易性

由上面可以得出:

Z^{T M} ∙ Z^{T E} = η^{2} = (Z^{T E M})^{2}

$Z^{TM}\bullet Z^{TE}=\eta^2 =(Z^{TEM})^2$
可以看到TE和TM波的波阻抗具有互易性

矩形波导

这里也是要做纵横关系式求解的最后一步,代入边界条件
由前面就可以知道,矩形波导不能传播TEM波
首先假设矩形波导的数学模型:
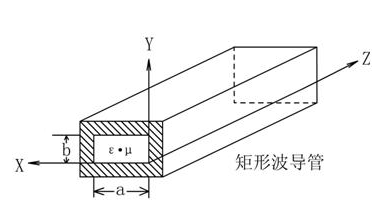
assumption
长a宽b壁导体
先上一张图辅助一下大家后面看边界条件的法向还是切向
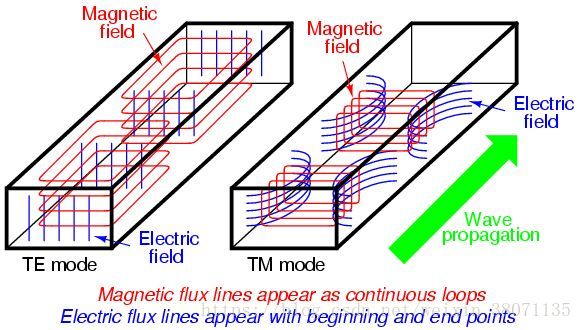
bodao

TM(图的右边)

边界条件:

(\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + k_{c}^{2}) E_{z} (x, y) = 0

$(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+k_c^2)E_z(x,y)=0$

{\begin{cases} E_{z} |_{x = 0} = 0, E_{z} |_{x = a} = 0 \\ E_{z} |_{y = 0} = 0, E_{z} |_{y = b} = 0 \end{cases}

$\begin{cases}E_z|_{x=0}=0,\quad E_z|_{x=a}=0 \\ E_z|_{y=0}=0,\quad E_z|_{y=b}=0\end{cases}$
其中

k_{c}^{2} = γ^{2} + k^{2}

$k_c^2=\gamma^2+k^2$ 称为截止波数.
公式的意义是很明确的:
传播TM波的时候矩形波导的边界都没有电场强度
以下是我以为的原因(有异议可以评论,大家互相学习一下)
1. 一个原因(一对边)在于,边界条件中,法向的电场强度连续,而理想导体内部没有电磁场
2. 另一对边是因为,上一章说过的趋肤效应导致的,而由于是

σ = \infty

$\sigma=\infty$ 所以就为0了

纵向解

由于我们想求的纵横关系式中,x和y是独立分开的.所以假设:

E_{z} (x, y) = X (x) Y (y)

$E_z(x,y)=X(x)Y(y)$
代入波动方程并化成常微分方程得:

\frac{d^{2} X}{d x^{2}} + k_{x}^{2} X = 0

$\frac {d^2 X}{dx^2}+k_x^2 X=0$

\frac{d^{2} Y}{d x^{2}} + k_{y}^{2} Y = 0

$\frac {d^2 Y}{dx^2}+k_y^2 Y=0$
其中:

k_{c}^{2} = k_{x}^{2} + k_{y}^{2}

$\quad \quad k_c^2=k_x^2+k^2_y$
显然特征方程的根是两个纯虚数,故设通解:

X (x) = A s i n k_{x} x + B c o s k_{x} x

$X(x)=Asink_x x +Bcosk_x x$

Y (y) = C s i n k_{y} y + D c o s k_{y} y

$Y(y)=Csink_y y +Dcosk_y y$

分别代入边界条件可得(书上P176):

E_{z} (x, y) = E_{0} s i n \frac{m π}{a} x s i n \frac{n π}{b} y, m, n = 1, 2, 3......

$E_z(x,y)=E_0 sin\frac{m\pi}{a}x sin \frac{n\pi}{b}y,\quad m,n=1,2,3......$
其中:

E_{0} = A C

$\quad\quad \quad E_0=AC$ 由激励源强度确定
大概的思路是先带入x=0和y=0那两条,算出B,D=0再代入剩下两条即可.

横向解

现在求出了 $E_z$ 的表达式,显然,代入一般情况可得:

E_{x} = - \frac{γ}{k_{c}^{2}} (\frac{m π}{a}) E_{0} c o s \frac{m π}{a} x s i n \frac{n π}{b} y

$E_x=-\frac{\gamma}{k_c^2}(\frac{m\pi}{a})E_0 cos\frac{m\pi}{a}xsin\frac{n\pi}{b}y$

E_{y} = - \frac{γ}{k_{c}^{2}} (\frac{n π}{b}) E_{0} s i n \frac{m π}{a} x s i n \frac{n π}{b} y

$E_y=-\frac{\gamma}{k_c^2}(\frac{n\pi}{b})E_0 sin\frac{m\pi}{a}xsin\frac{n\pi}{b}y$

H_{x} = \frac{j ω ε}{k_{c}^{2}} (\frac{n π}{b}) E_{0} s i n \frac{m π}{a} x c o s \frac{n π}{b} y

$H_x=\frac{j\omega\varepsilon}{k_c^2}(\frac{n\pi}{b})E_0 sin\frac{m\pi}{a}xcos\frac{n\pi}{b}y$

H_{y} = \frac{j ω ε}{k_{c}^{2}} (\frac{m π}{a}) E_{0} s i n \frac{n π}{b} x c o s \frac{m π}{a} y

$H_y=\frac{j\omega\varepsilon}{k_c^2}(\frac{m\pi}{a})E_0 sin\frac{n\pi}{b}xcos\frac{m\pi}{a}y$
其中:

k_{c} = \sqrt{γ^{2} + k^{2}} = \sqrt{k_{x}^{2} + k_{y}^{2}} = \sqrt{(\frac{m π}{a})^{2} + (\frac{n π}{b})^{2}}

$k_c=\sqrt{\gamma^2+k^2}=\sqrt{k_x^2+k_y^2}=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}$
由TE,TM的存在条件可以知道,当m=n=0时,方程无意义

TE(图的左边)

由于和TM是同一个套路,这里就直接给公式了:

边界条件

(\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + k_{c}^{2}) H_{z} (x, y) = 0

$(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+k_c^2)H_z(x,y)=0$

{\begin{cases} H_{z} |_{x = 0} = 0, H_{z} |_{x = a} = 0 \\ H_{z} |_{y = 0} = 0, H_{z} |_{y = b} = 0 \end{cases}

$\begin{cases}H_z|_{x=0}=0,\quad H_z|_{x=a}=0 \\ H_z|_{y=0}=0,\quad H_z|_{y=b}=0\end{cases}$

纵向解

H_{z} (x, y) = H_{0} c o s \frac{m π}{a} x c o s \frac{n π}{b} y, m, n = 1, 2, 3......

$H_z(x,y)=H_0 cos\frac{m\pi}{a}x cos\frac{n\pi}{b}y,\quad m,n=1,2,3......$

横向解

E_{x} = \frac{j ω ε}{k_{c}^{2}} (\frac{n π}{b}) H_{0} c o s \frac{m π}{a} x s i n \frac{n π}{b} y

$E_x=\frac{j\omega\varepsilon}{k_c^2}(\frac{n\pi}{b})H_0 cos\frac{m\pi}{a}xsin\frac{n\pi}{b}y$

E_{y} = - \frac{j ω ε}{k_{c}^{2}} (\frac{m π}{a}) H_{0} s i n \frac{m π}{a} x c o s \frac{n π}{b} y

$E_y=-\frac{j\omega\varepsilon}{k_c^2}(\frac{m\pi}{a})H_0 sin\frac{m\pi}{a}xcos\frac{n\pi}{b}y$

H_{x} = \frac{γ}{k_{c}^{2}} (\frac{m π}{a}) H_{0} c o s \frac{n π}{b} y s i n \frac{m π}{b} x

$H_x=\frac{\gamma}{k_c^2}(\frac{m\pi}{a})H_0 cos\frac{n\pi}{b}ysin\frac{m\pi}{b}x$

H_{y} = \frac{γ}{k_{c}^{2}} (\frac{n π}{b}) H_{0} s i n \frac{m π}{a} x s i n \frac{n π}{b} y

$H_y=\frac{\gamma}{k_c^2}(\frac{n\pi}{b})H_0 sin\frac{m\pi}{a}xsin\frac{n\pi}{b}y$
同理:m=n=0时,公式无意义

横场分布的物理特性

这里对应的是P178,下面列举出来只作复习回想用:

沿x,y的驻波性和z向的行波性

平面波的非均匀性

场的多模性

模式的兼并性

模式的阶次性

导波的纵场传输特性*

截止性(高通特性)

之前在一般传输特性就讲过这个问题,只是k可以由m和n给出,所以回代得:

k c = γ 2 + k 2 - - - - - - \sqrt = k 2 x + k 2 y - - - - - - \sqrt = (m π a) 2 + (n π b) 2 - - - - - - - - - - - - - \sqrt

$k_c=\sqrt{\gamma^2+k^2}=\sqrt{k_x^2+k_y^2}=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}$

f c - k c 2 π ε μ - - \sqrt = 1 2 ε μ - - \sqrt (m a) 2 + (n b) 2 - - - - - - - - - - - \sqrt

$f_c-\frac{k_c}{2\pi \sqrt{\varepsilon\mu}}=\frac1{2\sqrt{\varepsilon\mu}}\sqrt{(\frac ma)^2+(\frac nb)^2}$

λ c = 2 π k c = 2 ( m a ) 2 + ( n b ) 2 - - - - - - - - - - \sqrt

$\lambda_c=\frac{2\pi}{k_c}=\frac2{\sqrt{(\frac ma)^2+(\frac nb)^2} }$

色散性和滤波性

由上一个性质可以知道,在截取频率之前的波形都会因为传播常数的实部不为0而全部被去掉
所以当f> $f_c$ 时( $\alpha=0$ ):

β = ω 2 ε μ - (m π a) 2 - (n π b) 2 - - - - - - - - - - - - - - - - - - - \sqrt

$\beta=\sqrt{\omega^2\varepsilon\mu-(\frac{m\pi}{a})^2-(\frac{n\pi}{b})^2}$

λ g = 2 π β = 2 π ω 2 ε μ - ( m π a ) 2 - ( n π b ) 2 - - - - - - - - - - - - - - - - - \sqrt

$\lambda_g=\frac{2\pi}{\beta}=\frac{2\pi}{\sqrt{\omega^2\varepsilon\mu-(\frac{m\pi}{a})^2-(\frac{n\pi}{b})^2}}$

v p = ω β = ω ω 2 ε μ - ( m π a ) 2 - ( n π b ) 2 - - - - - - - - - - - - - - - - - \sqrt

$v_p=\frac{\omega}{\beta}=\frac{\omega}{\sqrt{\omega^2\varepsilon\mu-(\frac{m\pi}{a})^2-(\frac{n\pi}{b})^2}}$

阻抗双重性

这个由截止性就知道,低于截止频率的波阻抗呈阻性,高于的呈电抗性:

Z T M = γ j ω ε = ⎧ ⎩ ⎨ ⎪ ⎪ 1 ω ε ω 2 ε μ - (m π a) 2 - (n π b) 2 - - - - - - - - - - - - - - - - - \sqrt = R T M, f > f c - j 1 ω ε (m π a) 2 + (n π b) 2 - ω 2 ε μ - - - - - - - - - - - - - - - - - \sqrt = - j X T M c, f < f c

$Z^{TM}=\frac{\gamma}{j\omega\varepsilon}=\begin{cases}\frac1{\omega\varepsilon}\sqrt{\omega^2\varepsilon\mu-(\frac {m\pi}{a})^2-(\frac{n\pi}{b})^2}=R^{TM},\quad\quad \quad\quad f>f_c\\ -j\frac1{\omega\varepsilon}\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2-\omega^2\varepsilon\mu}=-jX_c^{TM},\quad \quad f<f_c\end{cases}$

Z T E = j ω μ γ = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ 1 ω μ 1 ω 2 ε μ - ( m π a ) 2 - ( n π b ) 2 \sqrt = R T M, f > f c j ω μ 1 ( m π a ) 2 + ( n π b ) 2 - ω 2 ε μ \sqrt = j X T M c, f < f c

$Z^{TE}=\frac{j\omega\mu}{\gamma}=\begin{cases}\frac1{\omega\mu}\frac1{\sqrt{\omega^2\varepsilon\mu-(\frac {m\pi}{a})^2-(\frac{n\pi}{b})^2}}=R^{TM},\quad\quad \quad\quad\quad\quad\quad f>f_c\\ j\omega\mu\frac1{\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2-\omega^2\varepsilon\mu}}=jX_c^{TM},\quad \quad\quad\quad\quad\quad\quad f<f_c\end{cases}$

主模 $TE_{10}$ 的传输特性

用主模传输的重点问题在于单模传输 单模传输 单模传输 单模传输

场分布

至于为什么 $TE^{10}$ 是主模的话,就不说了,你只要把 m,n的各个值代进去纵横关系式,就可以知道了

E y = ω μ a π H 0 s i n π a x c o s (ω t - β z - π 2)

$E_y=\frac{\omega\mu a}{\pi}H_0sin{\frac{\pi}ax}cos(\omega t-\beta z-\frac\pi2)$

H x = β a π H 0 s i n π a x c o s (ω t - β z + π 2)

$H_x=\frac{\beta a}{\pi}H_0sin{\frac{\pi}ax}cos(\omega t-\beta z+\frac\pi2)$

H z = H 0 c o s π a x c o s (ω t - β z)

$H_z=H_0cos\frac\pi a xcos(\omega t-\beta z)$
…其他三个为0…

传输特性

根据前面说的那些,代入m=1,n=0得:

f c = 1 2 a ε μ - - \sqrt

$f_c=\frac1{2a\sqrt{\varepsilon\mu}}$

λ c = 2 a

$\lambda_c=2a$

β = k 1 - (f c f) 2 - - - - - - - - \sqrt = ω 2 ε μ - (π a) 2 - - - - - - - - - - \sqrt

$\beta=k\sqrt{1-({\frac {f_c}{f}})^2}=\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}$

λ g = 2 π β = 2 π k 1 1 - ( f c f ) 2 - - - - - - - \sqrt = 2 π ω 2 ε μ - ( π a ) 2 - - - - - - - - - - \sqrt

$\lambda_g=\frac{2\pi}{\beta}=\frac{2\pi}{k}\frac1{\sqrt{1-({\frac {f_c}{f}})^2}}=\frac{2\pi}{\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}}$

v p = ω β = v 1 - ( f c f ) 2 - - - - - - - \sqrt = ω ω 2 ε μ - ( π a ) 2 - - - - - - - - - - \sqrt

$v_p=\frac{\omega}{\beta}=\frac v{\sqrt{1-({\frac {f_c}{f}})^2}}=\frac{\omega}{\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}}$

Z T E = η 1 1 - ( f c f ) 2 - - - - - - - \sqrt = ω μ 1 ω 2 ε μ - ( π a ) 2 - - - - - - - - - - \sqrt

$Z^{TE}=\eta\frac1{\sqrt{1-({\frac {f_c}{f}})^2}}=\omega\mu\frac1{\sqrt{\omega^2\varepsilon\mu-(\frac{\pi}{a})^2}}$

结语

因为这里写了比较多的波动方程,所以会有点长!