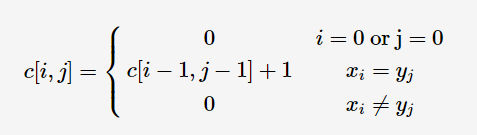最长公共子序列
Ax= a1,a2,……ax, By= b1,b2,……by, LCS(m,n)表示它们的最长公共子序列长度。L(x, y)表示Ax和By的一个最长公共子序列。
令x表示子序列考虑最后一项
(1) t = Ax = By
那么它们L(x,y)的最后一项一定是这个元素
此时:LCS(Ax, By) = LCS(x - 1, y - 1) + 1
(2) Ax ≠ By
仍然设t = L(Ax, By), 或者L(Ax, By)是空序列(这时t是未定义值不等于任何值)。
则t ≠ Ax和t ≠ By至少有一个成立,因为t不能同时等于两个不同的值!
如果t ≠ Ax,
则:L(x, y)= L(x - 1, y)
LCS(x,y) = LCS(x – 1, y)
如果t ≠ By,
L(x, y)= L(x , y - 1)
LCS(x,y) = LCS(x, y – 1)
可是,我们事先并不知道t,由定义,我们取最大的一个,因此这种情况下,有LCS(x,y) = max(LCS(x – 1, y) , LCS(x, y – 1))。
所以:
LCS(x,y) =
(1) LCS(x - 1,y - 1) + 1 如果Ax = By
(2) max(LCS(x – 1, y) , LCS(x, y – 1)) 如果Ax ≠ By
(3) 0 如果x = 0或者y = 0(一个空序列和任何序列的最长公共子序列都是空序列)
到此我们求出了计算最长公共子序列长度的递推公式。
0 1 2 3 4 5 j
i 0
1
2
3
4
i=j=0时,dp[i][j]=0
A[i]=B[j]时(从1计数),dp[i][j]=dp[i-1][j-1]+1
A[i]!=B[j]时,dp[i][j]=max(dp[i][j-1],dp[i-1][j])
int findLCS(string A, int n, string B, int m) {
int table[n + 1][m + 1];
for(int i=0;i<=n;i++)
table[i][0]=0;
for(int i=0;i<=m;i++)
table[0][i]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(A[i-1]==B[j-1])
table[i][j]=table[i-1][j-1]+1;
else
table[i][j]=max(table[i][j-1],table[i-1][j]);
}
}
return table[n][m];
}最长公共字串
明白了最长公共子序列,这个问题就很好理解了,重要的是找到转移方程:
class LongestSubstring {
public:
int findLongest(string A, int n, string B, int m) {
int res=0;
int c[n+1][m+1];
for(int i=0;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
if(i==0||j==0)
c[i][j]=0;
else if(A[i-1]==B[j-1])
{
c[i][j]=c[i-1][j-1]+1;
res=max(c[i][j],res);
}
else
c[i][j]=0;
}
}
return res;
}
};机器人走方格
有一个XxY的网格,一个机器人只能走格点且只能向右或向下走,要从左上角走到右下角。请设计一个算法,计算机器人有多少种走法。
解题思路:
对于当前的每一步F(x , y),一定是从F(x-1 , y)或F(x , y-1)走过来的。
假设机器人走到F(x-1 , y)有m种走法,走到F(x , y-1)有n种走法,则走到F(x , y)有m+n种走法。
这就是问题核心。
关于初值问题:
即:只有一行或者只有一列时,怎么走?
走法当然是只有一种。所以初始化F(0 , i)与F(j, 0)为1
法一:递归
int countWays(int x, int y) {
//递归
if(x==0&&y==0)
return 0;
else if(x==1||y==1)
return 1;
else
return countWays(x-1,y)+countWays(x,y-1);
}很好理解,可惜效率不高,当方格数变多时,耗时过多。
所以——铛铛铛铛!所有的递归都可以改写成循环(就看你会不会写,哼~)。
法二:动态规划
int uniquePaths(int m, int n) {
vector<vector <int> > F(m ,vector<int>(n,1));
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
F[i][j]=F[i-1][j]+F[i][j-1];
}
}
return F[m-1][n-1];
}分析:vector二维数组保存走到每个方格的走法数
双层for循环在更新走到每个方格的走法数
写到这里,脑海中灵光一闪!爬楼梯不也是这么回事嘛!
爬楼梯问题
你正在爬楼梯,需要n步才能达到顶峰。每次只能爬1或2步。 你可以通过多少不同的方式登顶?
动态规划法:
int climbStairs(int n) {
int dp[n + 1];
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}当然这个也可以用递归,太简单就不写了。
总结:
嘤嘤嘤,这是第一次对动态规划问题有了一定理解。
再接再厉!我要加油!
参考来自:https://blog.csdn.net/lz161530245/article/details/76943991