支持向量机（中）

这篇博客为大家介绍第二类支持向量机，线性支持向量机

上一篇博客中已经为大家介绍过线性可分支持向量机，其处理的是线性可分的样本集合，这篇博客主要为大家介绍线性支持向量机，主要处理的是线性不可分的样本集合，但最终构建的还是线性的分类超平面。

对于线性不可分的数据集，我们如果还采用线性可分支持向量机的目标函数和约束条件肯定是不可行的，因为，对于线性不可分的数据，我们构建的线性分类超平面一定会出现误分类点，而对于误分类点其几何间隔一定小于1（实际上是一个负值），这样便不能够满足线性可分情况下的约束条件了，因此如果采用线性可分支持向量机的求解策略是永远也找不到一个超平面的，因为总有不满足约束条件的样本点的存在。

那么对于这样的情况，我们该采取什么样的策略呢？

实际上，我们的处理思路也很简单，只需要在线性可分支持向量机的约束最优化问题上稍作改动就构造出了线性支持向量机的原始约束最优化问题。

我们的解决思路就是加入松弛变量 $\xi _i\geq 0$ 。那么 $\xi _i$ 是什么呢？在上篇博客中，我们说明了，函数间隔可以相对的表示某个样本点分类正确的确信度，现在我们以函数间隔1所对应的分类正确的确信度为基准确信度， $\xi _i$ 衡量了某个样本点的函数间隔距离1还差多少距离，也可以理解为距离基准确信度还差多少确信度。当然我们希望 $\xi _i$ 这个差距尽可能小。因此，对于函数间隔小于1的样本点，其 $\xi _i> 0$ ，而对于函数间隔大于等于1的样本点，其 $\xi _i= 0$ 。根据下图我们来更加直观的说明到底 $\xi _i$ 代表了什么：

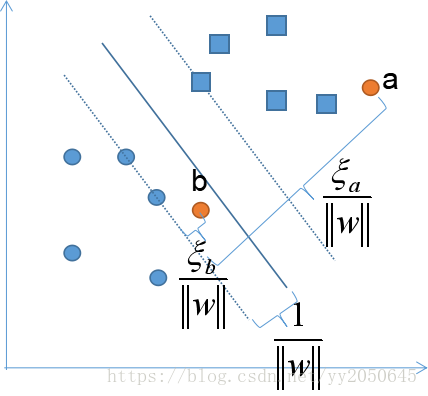
如上图所示，这是一个线性不肯分的样本集，a为误分类点，b为在分割边界和分类超平面之间的样本点，分类超平面关于这两个样本点的几何间隔均小于 $\frac{1}{\left \| w \right \|}$ ，而我们要求样本点的几何间隔均大于 $\frac{1}{\left \| w \right \|}$ ，因此，此时我们会在这些样本点的几何间隔的基础上加上 $\frac{\xi_i}{\left \| w \right \|}> 0$ 这样一个正值，使得这些样本点的几何间隔均大于等于 $\frac{1}{\left \| w \right \|}$ 。

用数学语言对上述过程进行描述就是：

$\frac{y_i(wx_i+b)}{\left \| w \right \|} + \frac{\xi_i}{\left \| w \right \|}\geq \frac{1}{\left \| w \right \|}, \xi_i\geq 0\;\;i=1, ..., N$

化简后得到：

$y_i(wx_i+b)+ \xi_i\geq 1, \xi_i\geq 0\;\;i=1, ..., N$

然而，对于所有函数间隔小于1的样本点，其都对应着一个 $\xi _i> 0$ ，我们将这些 $\xi _i> 0$ 大于0进行累加后得到一个累加值 $\sum_{i=1}^{N} \xi _i$ （此处采用了所有样本点的 $\xi _i$ 的累加，是因为对于那些已经满足函数间隔大于1的样本点的 $\xi _i= 0$ ），这个累加值表示了对于这些函数间隔不足1的样本点，其距离1差距的总和，当然我们是希望这个差距尽可能的小，因此，我们在目标函数变为了：

$min\;\frac{1}{2}\left \| w \right \|^2$

$min\sum_{i=1}^{N}\xi_i$

成为了一个多目标规划问题，当我们得出这个目标函数后我们再思考我们之前所说的， $\sum_{i=1}^{N} \xi _i$ 尽可能的小是否正确呢？显然这是不正确的，因为在相同约束条件下，我们使得 $\sum_{i=1}^{N} \xi _i$ 尽可能小了，那么 $\frac{1}{2}\left \| w \right \|^2$ 便会增大，也就是说，SVM模型的边际距离就会减小，这样便使得模型的泛化能力下降，而我们想要得到的是一个帕累托最优解。

为此，我们可以将其进行合并转换为单目标规划问题：

$min \frac{1}{2}\left \| w \right \|^2+C\sum_{i=1}^{N}\xi_i$

在这里我们加入了一个常数C，这是为了权衡两个目标，如果C很大，在求解过程中 $\sum_{i=1}^{N} \xi _i$ 就越受重视，那么为了使得目标函数足够小， $\sum_{i=1}^{N} \xi _i$ 的值便不会很大，反之如果C很小，则 $\frac{1}{2}\left \| w \right \|^2$ 会更受重视，因此， $\frac{1}{2}\left \| w \right \|^2$ 便不会很大，这样通过一个常数C，我们就达到了对二者进行调和的作用（实际上是对于模型泛化能力和训练准确率的一个权衡）。最终我们便得到了线性支持向量机的约束最优化问题，如下所示：

$\underset{w,b,\xi}{min}\; \frac{1}{2}\left \| w \right \|^2+C\sum_{i=1}^{N}\xi_i$

$s.t.\left\{\begin{matrix} y_i(wx_i+b)\geq 1-\xi_i,\;\;i=1, 2, ..., N\\ \xi_i\geq 0,\;\;i=1, 2, ..., N \end{matrix}\right.$

我们只需要求出上述问题的最优解 $w^*$ 和 $b^*$ 就能够得到最优分类超平面 $w^*x+b^*=0$ ，从而构造出最终的支持向量机模型：

$f(x)=sign(w^*x+b^*)$

其实对于上述约束最优化问题的求解套路和线性可分支持向量机是一样的：

获取原问题的对偶问题
求解对偶问题的最优解
根据对偶问题最优解以及一些定理求得原问题最优解

接下来，我们先构造原问题

针对以上的约束最优化问题，我们构造拉格朗日函数，如下所示：

$L(w,b,\xi,\alpha,\mu)=\frac{1}{2}\left \| w \right \|^2 + C\sum_{i=1}^{N}\xi_i-\sum_{i=1}^{N}\alpha_i[y_i(wx_i+b)+\xi_i-1] - \sum_{i=1}^{N}\mu_i\xi_i$

其中 $\alpha_i\geq 0$ 以及 $\mu_i\geq 0$ 为拉格朗日乘子，因此原问题如下所示：

$\underset{w,b,\xi}{min}\;\underset{\alpha,\mu}{max}\;L(w,b,\xi,\alpha,\mu)$

根据原问题，我们可以得到对偶问题，如下所示：

$\underset{\alpha,\mu}{max}\;\underset{w,b,\xi}{min}\;L(w,b,\xi,\alpha,\mu)$

首先我们需要求解 $\underset{w,b,\xi}{min}\;L(w,b,\xi,\alpha,\mu)$ ，我们构造如下方程组：

$\left\{\begin{matrix} \nabla_wL(w,b,\xi,\alpha,\mu)=-\sum_{i=1}^{N}\alpha_iy_ix_i+w=0\\ \nabla_bL(w,b,\xi,\alpha,\mu)=-\sum_{i=1}^{N}\alpha_iy_i=0\\ \nabla_{\xi}L(w,b,\xi,\alpha,\mu)=C-\alpha-\mu=0 \end{matrix}\right.$

求解得到：

$\left\{\begin{matrix}w=\sum_{i=1}^{N}\alpha_iy_ix_i\\ \sum_{i=1}^{N}\alpha_iy_i=0\\C-\alpha-\mu=0 \end{matrix}\right.$

将以上结果带入到拉格朗日函数中得到了：

$\underset{w,b,\xi}{min}\;L(w,b,\xi,\alpha,\mu)=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^{N}\alpha_i$

因此对偶问题 $\underset{\alpha,\mu}{max}\;\underset{w,b,\xi}{min}\;L(w,b,\xi,\alpha,\mu)$ 可以化简为：

$\underset{\alpha,\mu}{max}\;-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^{N}\alpha_i$

$\left\{\begin{matrix} \sum_{i=1}^{N}\alpha_iy_i=0\\ C-\alpha_i-\mu_i=0,\;\;i=1,...,N\\\alpha_i\geq 0,\;\;i=1,...,N\\\mu_i\geq 0,\;\;i=1,...,N \end{matrix}\right.$

将上述最优化问题化简，等价于下式：

$\underset{\alpha,\mu}{max}\;-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^{N}\alpha_i$

$\left\{\begin{matrix} \sum_{i=1}^{N}\alpha_iy_i=0\\ 0\leq \alpha_i\leq C,\;\;i=1,...,N \end{matrix}\right.$

此时，我们假设对偶问题的最优解为 $\alpha^*=(\alpha_1^*,\alpha_2^*,...,\alpha_N^*)$ ， $\mu^*=C-\alpha^*$ ，假设原问题最优解为 $w^*$ ， $b^*$ ， $\xi^*$ ，则对偶问题和原问题应该满足如下约束：

$\left\{\begin{matrix} \nabla_wL=w^*-\sum_{i=1}^{N}\alpha_i^*y_ix_i=0\\ \nabla_bL=-\sum_{i=1}^{N}\alpha_i^*y_i=0\\ \nabla_{\xi_i}L=C-\alpha_i^*-\mu_i^*=0\\ \mu_i^*\xi_i^*=0\\\alpha_i^*[y_i(w^*x_i+b^*)+\xi_i^*-1]= 0 \\ y_i(w^*x_i+b^*)+\xi_i^*-1\geq 0\\ \xi^*\geq 0\\ \alpha_i^*\geq 0\\ \mu_i^*\geq 0\end{matrix}\right.$

上述条件中，第四第五个式子是根据对偶理论中的互补松弛定理得来的，通过上述条件，我们可以求得原问题的解 $w^*$ ， $b^*$ ，表达式如下所示：

$\left\{\begin{matrix}w^*=\sum_{i=1}^{N}\alpha_i^*y_ix_i\\b^*=y_j-\sum_{i=1}^{N}y_i\alpha_i^*(x_i\cdot x_j) \end{matrix}\right.$

上式中， $y_j$ 为某一 $0< \alpha_j^*< C$ 所对应的样本点的样本标记。

在这里，为了让大家更加明确的了解 $b^*$ 是如何得出的，这里给出 $b^*$ 的推导过程，如下所示：

若某一 $\alpha_j^*$ 满足 $0< \alpha_j^*< C$ ，则有互补松弛定理可知：

$\alpha_j^*[y_j(w^*x_j+b^*)+\xi_j^*-1]= 0$

而我们根据最优解所满足的条件可知：

$\mu_j^*\xi_j^*=(C-\alpha_j^*)\xi_j^*=0$

因此，我们可以得出：

$\xi_j^*=0$

所以：

$y_j(w^*x_j+b^*)+\xi_j^*-1= y_j(w^*x_j+b^*)-1=y_i(w^*x_j+b^*)-y_j^2=0$

再将 $w^*$ 带入上式化简后便可求得 $b^*$ 的值，此时我们便构造出了分类超平面 $w^*x+b^*= 0$ ，最终我们构造出的线性支持向量机模型如下所示：

$f(x) = sign(w^*x+b^*)$

接下来，我们再给出线性支持向量机中支持向量的定义：

我们定义 $\alpha_j^*> 0$ 所对应的样本点就是线性支持向量机的支持向量：

若 $0< \alpha_j^*< C$ ，根据互补松弛定理我们很容易能够得出 $y_j(w^*x_j+b^*)= 1$ ， $0< \alpha_j^*< C$ 对应的样本点都落在了边界平面上，这些样本点属于支持向量。
$\alpha_j^*= C$ ，则 $\mu_j^*=0$ ，所以 $\xi_j^*\geq 0$ ，根据互补松弛定理可得 $\alpha_j^*[y_j(w^*x_j+b^*)+\xi_j^*-1]= 0$ ，因此 $y_j(w^*x_j+b^*)+\xi_j^*-1= 0$ ，若 $\xi_j^*= 0$ ，则 $y_j(w^*x_j+b^*)-1= 0$ ，这些样本点也都落在边界平面上，他们也属于支持向量；若 $\xi_j^*> 0$ ，则对应的样本点落在边界平面之间或者误分类一侧，这也属于支持向量。

综上，线性支持向量机对应的支持向量落在边界平面上，或者是边界平面之间，亦或者是误分类一侧。

这里和线性可分支持向量机一样，分类超平面只由支持向量来决定，而非支持向量对于超平面的构建不起作用。

最后，我们不考虑之前所构造的约束最优化问题的目标函数，假设我们要重新来定义支持向量机的损失函数，该如何定义呢？我们显然是希望那些函数间隔不足1的样本点，与1的差距总和越小越好，但是与此同时，为了防止过拟合，我们将模型复杂度也考虑在内，我们通常认为，如果参数数值过于大，则模型越复杂，从而越容易出现过拟合现象，因此，我们也希望 $\left \| w \right \|^2$ 不要太大，因此我们便构造出如下损失函数：

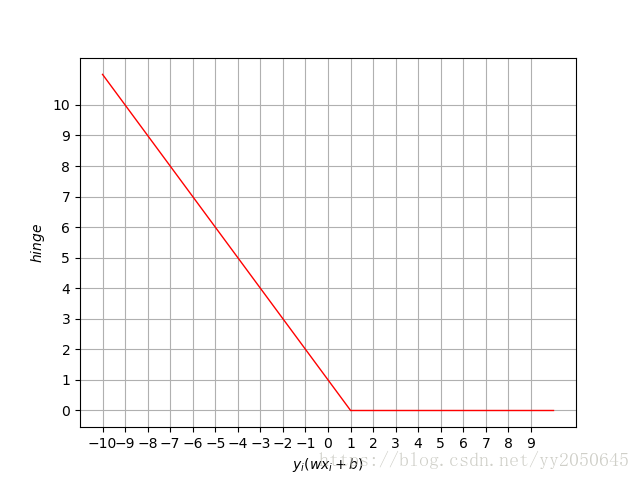
$loss=\sum_{i=1}^{N}[1-y_i(wx_i+b)]_++\lambda\left \| w \right \|^2$

我们定义：

$[z]_+=\left\{\begin{matrix} z,\;\;z> 0\\ 0,\;\;z\leq 0 \end{matrix}\right.$

$[1-y_i(wx_i+b)]_+$ 就是我们常说的支持向量机的合页损失函数，其函数图像如下图所示：

到这里，线性支持向量机就介绍完毕了，如有不足之处，请大家多多指正。下一篇博客将介绍非线性支持向量机。

支持向量机（中）

猜你喜欢