番外篇2.3 图像处理与深度学习 - 模式识别

在谈R-CNN之前，应该要先总结一下模式识别。
模式识别主要是对已知数据样本的特征发现和提取，比如人脸识别、雷达信号识别等，强调从原始信息中提取有价值的特征，在机器学习里面，好的特征所带来的贡献有时候远远大于算法本身的贡献。在番外篇中，我们使用过opencv中已经训练好的分类器，这也是模式识别的一种。
模式识别从处理问题的性质和解决问题的方法角度，可以分为有监督（分类）与无监督（聚类）两种。二者的主要差别在于，样本是否有labels。一般说来，有监督的分类往往需要提供大量带有labels的样本，但在实际问题中，这是比较困难的，因此研究无监督的分类十分重要。（当然，模式识别已经是比较老的技术，当有监督的分类有用武之地时，更有效的神经网络已经出现了，生不逢时呀）

1.1 分类

1.1.1 K-Nearest Neighbour

首先就是K最近邻（K-NN），是一种比较简单，直观的分类算法，也是计算量很大的一种算法。该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。特别的，当k = 1时，该对象被分到离它最近的邻居所在的类中。不过这种算法有个缺点是，它对数据的局部结构敏感，容易过度拟合数据。作为简单的防止过拟合的方法一般都是赋给更近的邻居更大的权重，比如距离的倒数。
参数k的选择很依赖数据，k越大，越容易忽视噪声，但边界也会更模糊。一般可以用不同的k值来训练k-NN分类器，然后验证哪个效果最好。
如果是分两类，k最好选择一个奇数，这样不容易产生某一个点模棱两可的情况。
还有，这个分类器对输入特征值域敏感，如果引入无关的特征会降低分类的准确性。可以将数据归一化到[0, 1]或[-1, 1]的区间内来防止。

1.1.2 决策树算法

决策树算法的核心，是根据先验条件构造一颗最好的决策树，来预测类别。
举一个例子，一个公司评判员工有两个标准，一个是听话程度，一个是聪明程度；
我们靠这两个参数来区分是否是好员工；

聪明	听话	好员工
8	2	no
4	8	yes
8	5	yes
2	6	no

我们有几种方法来做区分。以一种为例：用听话程度来区分：
听话>=5 是树的左子树，听话<4是树的右叶子节点，右叶子节点均为坏员工；
再对左子树进行区分，聪明>3为左子树，聪明<=为右子树，左子树均为好员工，右子树均为坏员工；这样就完成了一种决策树。那如何判断决策树的好坏呢？
这种判断好坏的参数就是，信息熵增益。如果经过某个属性，划分后的数据信息熵下降最多，那么这种划分为最优。
如我现在用的方法，第一次划分前熵为：
-（2/4*log2(2/4)+2/4*log2(2/4)） = 1;
划分后右子节点熵为0，左子节点熵：
-（2/3*log2(2/3)+1/3*log2(1/3)）= 0.39+0.526 = 0.916；这个熵下降就是0.084。
第二次划分后，区分完毕，熵为0。（举的例子太弟弟了，不太明显，不过还算容易懂啦）
经过决策属性的划分后，数据的无序度越来越低，也就是信息熵越来越小。
具体就不细说啦 我们这可以说图像处理的，有点跑偏了。。顺便说一下，基于规则的分类器和这个大致相同，有兴趣的可以自己搜，就不在这里占用版面了。

1.1.3 贝叶斯分类

说贝叶斯，首先要说朴素贝叶斯。朴素贝叶斯如其名，非常朴素。核心思想就是对于待分类项，求解各个类别出现的概率，然后哪个概率最大，这个分类项就是那个类别。
当然，这个概率获得才是NB的核心。一般我们需要一个训练样本集，统计一下条件概率估计，然后如果每个条件对概率的影响互相不相关，我们就可以算出测试集中某一个样本的各类别概率，从而顺利分类了。朴素贝叶斯一个很重要的点就是每个条件对概率的影响互相不相关。然而这个在现实中几乎不可能，所以贝叶斯分类又有了新的成员：贝叶斯网络。类似决策树（不过这个树是事先确定而不是训练），贝叶斯在每个子叶片上（全部特征区分后的）计算概率，然后用这个概率作为测试集中某一个样本按照条件走下来之后的概率。 贝叶斯网络比朴素贝叶斯更复杂，而想构造和训练出一个好的贝叶斯网络更是异常艰难。但是贝叶斯网络是模拟人的认知思维推理模式，用一组条件概率函数以及有向无环图对不确定性的因果推理关系建模，因此其具有更高的实用价值。
贝叶斯网络要首先确定随机变量之间的拓扑结构。这也是一个容易出问题的环节。

1.1.4 支持向量机（SVM）

这才是重头戏嘛！偷别人一张图说明下：

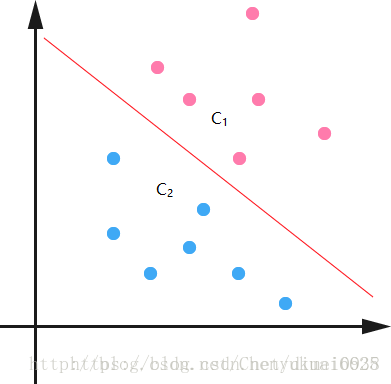
c1，c2分别是两个类，如何把这两个类区分开呢？就是在中间画条线（废话）
不过这个线其实很有讲究，画在哪里，角度如何呢？
这就是svm算法所研究的核心，核心思想是：让最近的样本点距离这个超平面最远（有点小绕）。那么，我们就有了目标函数：min（样本点i到超平面的距离）。
然后我们改变超平面的参数（这图上是线性的，就只有k，b两个），创造很多超平面，得到max（min（样本点i到超平面j的距离））。
这是一个凸二次规划问题，用拉格朗日对偶法可以解得。网上很多求解过程，看着都累，就不搬上来了，自己搜搜看。当这种方法可以区分的比较好，但是有异常点怎么办呢？svm算法引入了松弛变量的概念，给这个线性超平面一个可以改变的偏置，下面的点只要在这个偏置最大的时候被分类就可以，上面同理。当然，在计算超平面的时候，也要保证这个松弛变量尽量小。（SMO算法）
当样本完全线性不可分的时候怎么办呢？SVM又引入了一个概念：核函数。在我的理解例，核函数就是一个映射，把线性不可分的样本映射到一个线性可分的坐标系中，然后再用线性可分的方法来区分。核函数一般有多项式核和高斯核，除了特殊情况，一般高斯核被使用的最多，因为比较灵活啦。。
感觉也没啥好说的，不过好像蛮重要的诶，说一下python实现的思路：

from numpy import * 

def loadDataSet(filename): #读取数据
    dataMat=[]
    labelMat=[]
    fr=open(filename)
    for line in fr.readlines():
        lineArr=line.strip().split(' ')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat #返回数据特征和数据类别

def selectJrand(i,m): #在0-m中随机选择一个不是i的整数
    j=i
    while (j==i):
        j=int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):  #保证a在L和H范围内（L <= a <= H）
    if aj>H:
        aj=H
    if L>aj:
        aj=L
    return aj

def kernel(X, A, kTup): #核函数，输入参数,X:支持向量的特征树；A：某一行特征数据；kTup：('lin',k1)核函数的类型和参数
    m,n = shape(X)
    K = mat(zeros((m,1)))
    if kTup[0]=='lin': #线性函数
        K = X * A.T
    elif kTup[0]=='rbf': # 径向基函数(radial bias function)
        for j in range(m):
            deltaRow = X[j,:] - A
            K[j] = deltaRow*deltaRow.T
        K = exp(K/(-1*kTup[1]**2)) #返回生成的结果
    return K


#定义类，方便存储数据
class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # 存储各类参数
        self.X = dataMatIn  #数据特征
        self.labelMat = classLabels #数据类别
        self.C = C #软间隔参数C，参数越大，非线性拟合能力越强
        self.tol = toler #停止阀值
        self.m = shape(dataMatIn)[0] #数据行数
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0 #初始设为0
        self.eCache = mat(zeros((self.m,2))) #缓存
        self.K = mat(zeros((self.m,self.m))) #核函数的计算结果
        for i in range(self.m):
            self.K[:,i] = kernel(self.X, self.X[i,:], kTup)


def calcEk(oS, k): #计算Ek
    fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

#随机选取aj，并返回其E值
def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    oS.eCache[i] = [1,Ei]
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]  #返回矩阵中的非零位置的行数
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE): #返回步长最大的aj
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej


def updateEk(oS, k): #更新os数据
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]

#首先检验ai是否满足KKT条件，如果不满足，随机选择aj进行优化，更新ai,aj,b值
def innerL(i, oS): #输入参数i和所有参数数据
    Ei = calcEk(oS, i) #计算E值
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)): #检验这行数据是否符合KKT条件 参考《统计学习方法》p128公式7.111-113
        j,Ej = selectJ(i, oS, Ei) #随机选取aj，并返回其E值
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if (oS.labelMat[i] != oS.labelMat[j]): 
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H:
            print("L==H")
            return 0
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] 
        if eta >= 0:
            print("eta>=0")
            return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta 
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L) 
        updateEk(oS, j)
        if (abs(oS.alphas[j] - alphaJold) < oS.tol): 
            print("j not moving enough")
            return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
        updateEk(oS, i) #更新数据
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]<oS.C):
            oS.b = b1
        elif (0 < oS.alphas[j]<oS.C):
            oS.b = b2
        else:
            oS.b = (b1 + b2)/2.0
        return 1
    else:
        return 0


#SMO函数，用于快速求解出alpha
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #输入参数：数据特征，数据类别，参数C，阀值toler，最大迭代次数，核函数（默认线性核）
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:
            for i in range(oS.m): #遍历所有数据
                alphaPairsChanged += innerL(i,oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)) #显示第多少次迭代，那行特征数据使alpha发生了改变，这次改变了多少次alpha
            iter += 1
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs: #遍历非边界的数据
                alphaPairsChanged += innerL(i,oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        if entireSet:
            entireSet = False
        elif (alphaPairsChanged == 0):
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas

def testRbf(data_train,data_test):
    dataArr,labelArr = loadDataSet(data_train) #读取训练数据
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', 1.3)) #通过SMO算法得到b和alpha
    datMat=mat(dataArr)
    labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas)[0]  #选取不为0数据的行数（也就是支持向量）
    sVs=datMat[svInd] #支持向量的特征数据
    labelSV = labelMat[svInd] #支持向量的类别（1或-1）
    print("there are %d Support Vectors" % shape(sVs)[0]) #打印出共有多少的支持向量
    m,n = shape(datMat) #训练数据的行列数
    errorCount = 0
    for i in range(m):
        kernelEval = kernel(sVs,datMat[i,:],('rbf', 1.3)) #将支持向量转化为核函数
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b  #这一行的预测结果,注意最后确定的分离平面只有那些支持向量决定。
        if sign(predict)!=sign(labelArr[i]): #sign函数 -1 if x < 0, 0 if x==0, 1 if x > 0
            errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m)) #打印出错误率
    dataArr_test,labelArr_test = loadDataSet(data_test) #读取测试数据
    errorCount_test = 0
    datMat_test=mat(dataArr_test)
    labelMat = mat(labelArr_test).transpose()
    m,n = shape(datMat_test)
    for i in range(m): #在测试数据上检验错误率
        kernelEval = kernel(sVs,datMat_test[i,:],('rbf', 1.3))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr_test[i]):
            errorCount_test += 1
    print("the test error rate is: %f" % (float(errorCount_test)/m))

#主程序
def demo1():
    filename_traindata='C:\\Users\\Administrator\\Desktop\\data\\traindata.txt'
    filename_testdata='C:\\Users\\Administrator\\Desktop\\data\\testdata.txt'
    testRbf(filename_traindata,filename_testdata)

if __name__=='__main__':
    demo1()

代码来源：https://blog.csdn.net/csqazwsxedc/article/details/71513197（代码比较容易看懂）
总觉得要买一本《统计学习方法》呀，等找完工作再处理这些事情（希望能找到）

1.2 聚类

接下来说无监督的模式识别，也就是聚类。
聚类最著名，经典的应该就是k-means了，其他还有DBSCAN（基于密度）、CLIQUE（基于网络）、FCM（模糊c均值）等等等等，太多了，先说k-means，其他后面看心情吧，反正又不搞数据挖掘（目前），再说再说

1.2.1 k-means算法

k-means是一种基于距离聚类的算法。
k-means的算法核心思想是：
1.先选择k个点作为质心；
2.再把每个点指派到距离最近的质心，每进行一次，都重新计算一次每个簇的质心；
一直到簇的质心不发生变化或者达到最大迭代次数为止。
这个算法有一个很重要的问题，就是k值怎么定，k个质心选在哪里。
k值的话，对于可以确定K值不会太大但不明确精确的K值的场景，可以进行迭代运算，然后找出代价函数最小时所对应的K值，这个值往往能较好的描述有多少个簇类。 （不过，也不是最小的时候对应的k值最好，当代价函数下降的不明显时，就可以选择那个k值（肘部法则））
此外，还有用层次聚类方法预估计k值的，用canopy算法进行初始划分的，在这里先不仔细提。（简单说一下，canopy算法是先将相似的对象放到一个子集中，canopy可以互相重叠；对每个canopy可以使用传统的聚类。）
还有的方法是选取小样本（比如10000个中选取1000个）来预估计k值和质心的位置，目的都是一样，减少聚类时的计算量并优化结果（Mini Batch k-Means）。
对于初始质心的选取，最常见的就是随机，多次取，找到最好的值。这种策略简单，但计算量大，取决于数据集和簇的个数。
还有就是在取小样本的时候，可以用随机选一个点，然后选离重心最远的点作为下一个质点；然后再重复到合适位置。
还有一个方法，就是用层次聚类的方法提取几个簇，作为初始质心。当样本较小，且k值相对较小的时候才合适。
当然，用canopy算法也可以。。
k-means算法的优点在于，原理简单，超参只有一个k值，调节简单；扩展性强。速度还可以。
缺点在于，对k值太敏感，对初始质心位置敏感，对离群点敏感；当样本量大，时间开销非常大；不能处理所有类型的簇。
改进型有各种，比如bisecting K-means（二分k均值）； K-modes；K-prototype等。。这里就不列举了。。

1.2.2 DBSCAN

1.首先确定半径r和minPoints. 从一个没有被访问过的任意数据点开始，以这个点为中心，r为半径的圆内包含的点的数量是否大于或等于minPoints，如果大于或等于minPoints则改点被标记为central point,反之则会被标记为noise point。
2.重复1的步骤，如果一个noise point存在于某个central point为半径的圆内，则这个点被标记为边缘点，反之仍为noise point。重复步骤1，知道所有的点都被访问过。
优点：不需要知道簇的数量；可以发现任何形状的簇；可以找出异常点。
缺点：需要确定距离r和minPoints，调参较为复杂；如果簇间密度不同，不合适；样本集太大时，收敛时间较长。

1.2.3 CLIQUE

CLIQUE是基于网格的聚类算法。首先先以一个步长（参数1）分割整个域，然后扫描每个网格内的样本数目，判断是否是密集网格（阈值：参数2）。
然后就把聚类问题化简为类似空间内求01连通域问题，每一个联通域就是一个簇。
优点：高效；单遍数据扫描就可以完成目的。
缺点；两个参数，调参较为复杂；对不同密度的簇不合适；对于高维空间，效果会很不好。

1.2.4 基于GMM的EM聚类

GMM首先假设了数据点是呈高斯分布的，就像K-means假定数据点是圆分布。高斯分布是椭圆的，所以要更灵活一些。
要做聚类就要找到样本的均值和标准差，这时采用EM算法，过程是：
1. 首先选择簇的数量并随机初始化每个簇的高斯分布参数（期望和方差）。也可以先观察数据给出一个相对精确的均值和方差。
2. 给定每个簇的高斯分布，计算每个数据点属于每个簇的概率。一个点越靠近高斯分布的中心就越可能属于该簇。
3. 基于这些概率我们计算高斯分布参数使得数据点的概率最大化，可以使用数据点概率的加权来计算这些新的参数，权重就是数据点属于该簇的概率。
4. 重复迭代2和3直到在迭代中的变化不大。
GMMs的优点：GMMs使用均值和标准差，簇可以呈现出椭圆形而不是仅仅限制于圆形；GMMs是使用概率，所有一个数据点可以属于多个簇。例如数据点X可以有百分之20的概率属于A簇，百分之80的概率属于B簇。
行了行了 又说多了，本来想说图像检测的东西来着，一搞模式识别说了一大堆。。模式识别还有很多其他的方式，比如层次识别啊 模糊均值啊 请大家动动手指去百度吧（其实我有些也是百度来的，发出来是为了让自己更有印象）
图像检测下一节总结！