椭圆曲线加密(ECC)最大的优点就是使用比RSA短得多的密钥得到相同的安全性,因此可以减少处理负荷,使公钥密码的应用领域得到拓展。
1. 奇怪的对称性
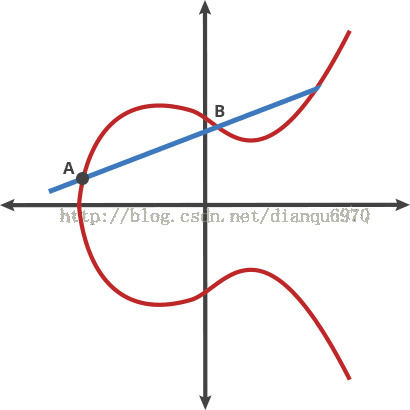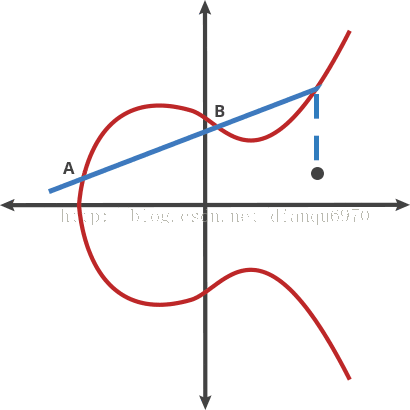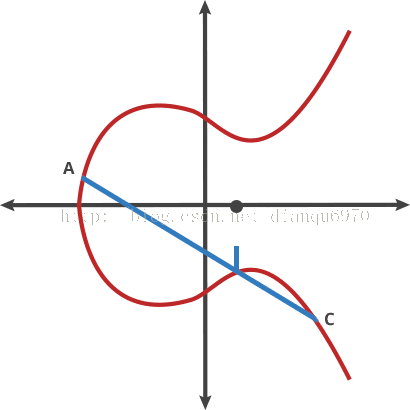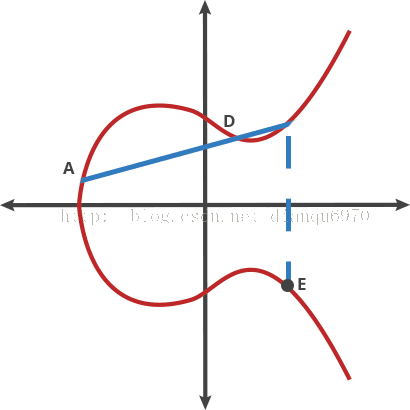
它是水平对称的。图形是关于x轴对称的。
更有趣的是,任何不垂直的直线最多与曲线有三个交点。
让我们把这个曲线想象成一个奇异的桌球游戏。在曲线上任取两个点,并画一条线进过他们,这个直线将再穿过曲线至多一个点。在这个桌球游戏中,拿一个球从A点射向B点,当它击中曲线时,这个球要么笔直向上弹(在x轴的下面)或者笔直向下弹(在x轴的上方),弹向曲线的另一边。
我们称这个经过两点的桌球叫“打点”。任何两个点通过打点可以得到一个新的点。
A dot B=C
我们可以反复这个规则:
A dot A=B
A dot B=C
A dot C=D
…
这说明了如果你有两个点,经过n次的打点之后将得到一个最终的点。仅仅知道原始点和最终点来找出n是很难的。为了继续拿这个桌球游戏来暗喻,一个人在随机的时间段内按照桌球的规则进行着这个游戏,这是很简单的。但是,如果另一个人在开始后的某段时间进入后,即使他看见了球终止的地方,和球起始的点,他也很难决定打点的次数,除非他全程在看着这个游戏。容易做,却很难解,这个是trapdoor函数的基础。
二、椭圆曲线离散对数在密码中的应用
公钥密码算法总要基于一个数学难题,比如RSA的依据是给定两个数p, q很容易相乘得到N, 而对n进行因式分解则相对困难的多。椭圆曲线密码体制(ECC)采用的数学难题则是求椭圆曲线加法群的离散对数问题,具体描述如下:
Q = kG
其中Q为椭圆曲线上的点, G为椭圆曲线上的基点,k 为小于n的整数,n为G的阶即, nG = O
根据上节提到的纯量乘法知道k, G不难求出Q, 但是给定Q, G求k就相对困难了,这就叫椭圆曲线加法群上的离散对数问题。
上述整数k,就是ECC私钥, Q为公钥, 可以利用此密钥对进行加密,解密,签名,验证等公私钥运算。
根据上节提到的纯量乘法知道k, G不难求出Q, 但是给定Q, G求k就相对困难了,这就叫椭圆曲线加法群上的离散对数问题。
上述整数k,就是ECC私钥, Q为公钥, 可以利用此密钥对进行加密,解密,签名,验证等公私钥运算。
三、ECDSA简单介绍
下面简单介绍一下基于GF(p)的椭圆曲线数字签名算法(ECDSA)
预备数据: h(待签名Hash值),公钥Q,私钥d
签名过程:
1. 选取一个随机数k;
2. 计算k = kmodn, 如果k =0返回第1步重新选取;
3. 计算kG = (x1, y1);
4. 计算r = x1mondn;
5. 如果r = 0返回第2步;
6. 计算s = k^-1*(h+ dr )modn;
7. 如果s = 0, 返回第2步;
其中(r, s)为签名结果。
验证过程:
1. 验证1=<r<=n-1, 若不成立返回false
2. 验证1=<s<=n-1, 若不成立返回false
3. 计算c = s^-1modn
4. 计算u1 = e’*c modn, u2 = r*c mon n
5. 计算u1*G+u2*Q = (x1, y1), 如果(x1, y1)为O 返回false
6. 计算v = x1modn;
7. 如果r != v 返回false
8. 返回true
基本原理:
椭圆曲线密码体制使用了在有限Abel群(Zp或者GF(2m))上构造的椭圆曲线,椭圆曲线在有限群的加法符号定义下成为一个单向陷门函数。
在有限群上的椭圆曲线在计算上没有显而易见的几何解释,但是可以将实数域上的椭圆曲线的几何解释移植过来。为了方便理解,先从实数域上的椭圆曲线开始讲解
1. 实数域上的椭圆曲线
椭圆曲线并不是椭圆,而是与椭圆周长的方程相似的三次方程。一般,椭圆曲线方程形为:
y2 + axy + by = x3 + cx2 + dx + e
对我们而言将方程限制为以下形式就已足够:
y2 = x3 + ax + b (10.1)
对于给定的a和b,对x的每一个值,需画出y的正值和负值。
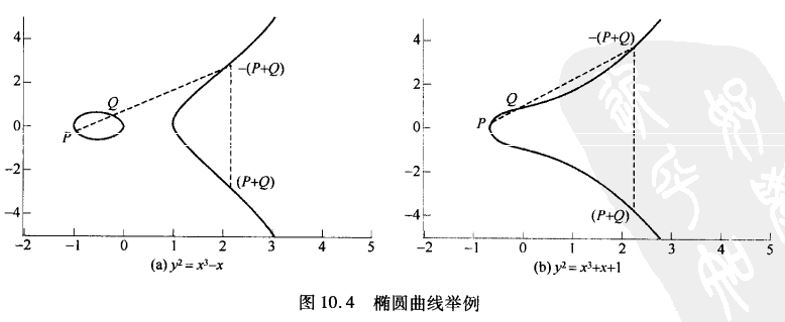
构造Abel群
将满足式(10.1)的所有点(x , y)和元素O(称为无穷远点或者零点的元素,后面会讨论这个概念)所组成的点集E(a , b)。上图中两条曲线分别可用集合E(-1 , 0)和E(1 , 1)表示。
若式(10.1)里的参数a和b满足
4a3 + 27b2 ≠ 0 (10.2)
则基于集合E(a , b)可以定义一个可交换群(Abel群),其加法的运算规则如下:
1、O是加法的单位元,有O = -O;对椭圆曲线上任何一点P,有P + O = P
2、点P (x , y)的负元-P = (x , -y)。注意这两点可以用一条垂直的线连接起来,并且P + (-P) = P - P = O
3、要计算坐标不同的P和Q之和,则在P和Q间作一条直线并找到与曲线的第三个交点R(显然存在唯一的交点R,除非这条直线与P或者Q相切,此时分别取R = P或者R = Q,与下述5相一致)。并定义如下三点上的加法:P + Q = -R。也就是,定义P + Q 为第三个交点相对于x轴的镜像
4、上述术语的几何解释也适用于具有相同x坐标的两个点P和 -P的情形。用一条垂直的线连接这两点,这可视为在无穷远点与曲线相交,因此有P + (-P) = O,与上述2相一致。
5、为计算点Q的两倍,画一条切线并找到另一交点S,则Q + Q = 2Q = -S。
加法的结论
1、对于不是互为负元的两个不同点P = (xP , yP) 和 Q = (xQ , yQ),连接它们的直线的斜率Δ= (yQ - yP)/(xQ - xP),我们可用如下表示和R = P + Q
xR =Δ2 - xP - xQ
yR =Δ(xP - xR) - yP (10.3)
2、计算一个点与它自身相加:P + P = 2P = R,则表达式为
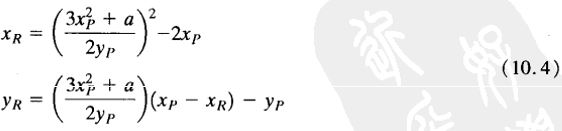
2. Zp上的椭圆曲线
对于Zp上的素曲线,我们使用三次方程,p为素数,其中的变量和系数自集合{0,1,···,p-1}取值,运算为模p运算。
对Zp上的椭圆曲线,如同实数情形一样,方程如下:
y2 mod p = (x3 + ax + b) mod p (10.5)
可以证明,若(x3 + ax + b) mod p无重复因子,则基于集合Ep(a , b)可定义一个有限Abel群,这等价于以下条件:
(4a3 + 27b2) mod p ≠ 0 (10.6)
注意,(10.6)与(10.2)具有相同的形式
Ep(a , b)上的加法运算构造与定义在实数上的椭圆曲线中的描述的代数方法是一致的。对任何点P , Q∈Ep(a , b)
1、P + O = P
2、若P = (xP , yP),则点(xP , -yP)是P的负元,记为 -P。例如对E23(1 , 1)上的点P = (13 , 7),有 -P = (13 , -7),而 -7 mod 23 = 16,因此,-P = (13 , 16),该点也在E23(1 , 1)上。
3、若P = (xP , yP),Q = (xQ , yQ),且P ≠ -Q则R = P + Q = (xR , yR)由下列规则确定:
xR =λ2 - xP - xQ
yR =λ(xP - xR) - yP
其中
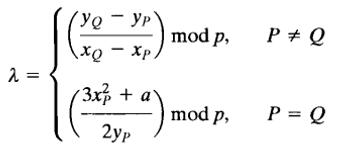
4、乘法定义为重复相加。如4P = P + P + P + P
为了确定各种椭圆曲线密码的安全性,需要知道定义在椭圆曲线上的有限Abel群中点的个数。在有限群Ep(a , b)中,点的个数N的范围是
p + 1 - 2p1/2 ≤ N ≤ p + 1 + 2p1/2
所以,Ep(a , b)上点的个数约等于Zp中元素的个数,即p个元素。
3. GF(2m)上的椭圆曲线
对于GF(2m)上的椭圆曲线,其变量和系数在GF(2m)内取值,且运算为GF(2m)里的运算。可以证明,GF(2m)上适合于椭圆曲线密码应用的三次方程与Zp上的三次方程有所不同,其形为:
y2 + xy = x3 + ax2 + b (10.7)
可以证明,只要b ≠ 0,则可基于集合E2m(a , b)可定义一个有限Abel群。对任何点P , Q∈E2m(a , b),加法的运算规则如下:
1、P + O = P
2、若P = (xP , yP),则P + (xP , xP + yP) = O。点(xP , xP + yP)是P的负元,记为 -P。
3、若P = (xP , yP),Q = (xQ , yQ),且P ≠ -Q,P ≠ Q则R = P + Q = (xR , yR)由下列规则确定:
xR =λ2 +λ+ xP + xQ + a
yR =λ(xP + xR) + xR + yP
其中

4、若P = (xP , yP),则R = 2P = (xR , yR)由下列规则确定:
xR =λ2 + λ+ a
yR =xP2 + (λ + 1)xR
其中
λ= xP + yP/xP
椭圆曲线密码学
考虑方程Q = kP,其中Q,P∈Ep(a , b),对给定的k和P计算Q比较容易,而对给定的Q和P计算k则很困难,这就是椭圆曲线的离散对数问题。
用椭圆曲线实现Diffie-Hellman密钥交换
首先,挑选一个大整数q以及式(10.5)或式(10.7)中的椭圆曲线参数a和b,这里q为素数p或者是形为2m的整数。由此可以定义出点的椭圆群Eq(a , b)
其次,在Eq(a , b)中挑选基点G = (x1 , y1),G的阶为一个非常大的数n。椭圆曲线上的点G的阶n是使nG = 0 成立的最小正整数。Eq(a , b)和G是该密码体制中通信各方均已知的参数
用户A和用户B之间完成密钥交换过程如下:
1、A选择一个小于n的整数nA作为其私钥,然后产生其公钥PA = nA × G。该公钥是Eq(a , b)中的一个点。B也类似地选择私钥nB并计算公钥PB
2、A产生秘密钥k = nA × PB,B产生秘密钥k = nB × PA
nA × PB = nA × (nB × G) = nB × (nA × G) = nB × PA
要破译这种体制,攻击者必须由G和kG计算k,这被认为很难。
椭圆曲线加/解密
首先,我们必须将要发送的消息明文m编码为形为(x , y)的点Pm,并对点Pm进行加密和其后的解密。注意,不能简单地将消息编码为点的x坐标或y坐标,因为并不是左右的坐标都在Eq(a , b)中。将消息m编码为点Pm的方法有很多种,存在比较直接的编码方法。
像密钥交换系统一样,加/解密系统也需要点G和椭圆群Eq(a , b)这些参数。每个用户选择一个私钥n,并产生公钥P = n × G
若A要将消息Pm加密后发送给B,则A随机选择一个正整数k,并产生密文Cm,该密文是一个点对:
Cm = {kG , Pm + kPB}
注意,此处A使用了B的公钥PB,B要对密文解密,则需用第二个点减去第一个点与B的私钥之积:
Pm + kPB - nB(kG) = Pm + k(nBG) - nB(kG) = Pm
椭圆曲线密码的安全性
ECC的安全性是建立在由kP和P确定k的困难程度之上的,这个问题称为椭圆曲线对数问题。Pollard rho方法是已知的求椭圆曲线对数最快的方法。下表从密码分析所需计算量的角度,通过给出可比较的密钥大小,比较了各种算法。在密钥长度相同时,ECC和RSA所执行的计算量差不多。因此,与具有同等安全性的RSA相比,由于ECC使用的密钥更短,所以ECC所需的计算量比RSA更小。
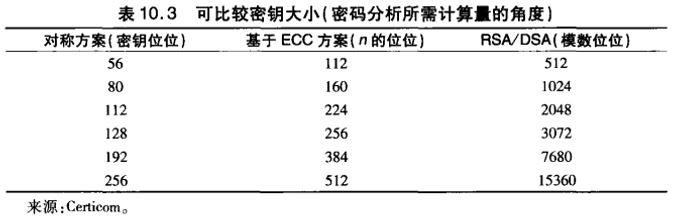
基于非对称密码的伪随机数生成器
由于非对称算法的速度比对称算法明显慢一些,所以非对称算法不用于生成可扩展的PRNG流,但是,对于生成短的伪随机序列,创建伪随机函数(PRT),非对称的方法还是很有用的。
Micali-Schnorr PRNG

该PRNG定义如下:
创建 选择素数p,q;n = pq;φ(n) = (p - 1)(q - 1),选择e使得gcd(e ,φ(n)) = 1。此外N =└log2n┘ + 1(n的位长度)。选择r,k使得r + k = N
种子 选择位长度为r的随机种子x0
生成 生成一个长为k × n的伪随机序列,将i从1到m,计算
yi = xi-1e mod n
xi = r , yi的最高有效位
zi = k , yi的最低有效位
输出 输出序列为z1 || z2 || ··· || zm
参数n,r,e,k的选择要遵循下面6个要求:
1、n = pq n是两个素数的乘积,在RSA中则是密码长度
2、1 < e < φ(n) ;gcd(e ,φ(n) ) = 1 确保映射s -> se mod n是一对一的
3、re ≥ 2N 确保求幂运算是有取模过程
4、r ≥ 2 防止密码攻击
5、k,r是8的倍数 应用方便
6、k ≥ 8;r + k = N 所有位都有效