引言
大多数使用公钥密码进行加密和数字签名的产品都使用的是RSA算法。为了保证RSA的安全性,密钥的位数一定会增加,这对使用RSA的应用有着很重的负担。
而椭圆曲线密码(elliptic curve cryptography)的出现代表:可以使用比RSA短的多的密钥得到相同的安全性,因此可以减少处理负荷。
但是ECC真的很难阐述,下面我简单整理一下基本原理,以求读者看后能有一个大概的了解就ok。
椭圆曲线方程
我们多多少少都学过一些椭圆的数学知识,但是其实椭圆曲线并不是椭圆,称为椭圆曲线知识因为它们与计算椭圆周长的方程相似,也是用3次方程2个变量来表示的,可以简单表示为
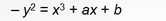
椭圆曲线的定义中还包含一个称为无穷远点或者零点的元素,极为O,我们先不讨论这个。
从这个方程中我们可以知道一点:椭圆曲线关于x轴对称,这很重要。
这条曲线大概是这样子的:
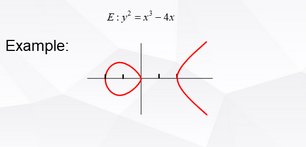

同时,在上图中还要说明的很重要的一点是P+Q= -R,可以这么理解:这条曲线上的所有点构成了一个Abel群,群的性质中有一条,任意两点之和还在这个这个群里面,在曲线图形上的体现就是,任意两点的连线与曲线的另一个交点的镜像是这两个点的和。(先记住,后面都是围绕这一点推导的)
此时可以利用斜率和某些代数运算计算出r的坐标

λ是P和Q的斜率
举一个例子:
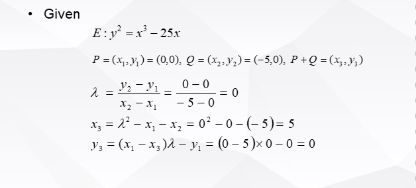
这样来看是不是就很容易理解了呢?
ok,那么继续,我们从椭圆曲线开始向密码延伸,密码应用中我们只简单将一个素曲线
素曲线的形式可以简单理解为在椭圆方程的两边同时取模mod p,然后再找符合条件的点
例如这是一个取模11例子

那么根据上面Abel群的性质,取模后同样是一个群,所以符合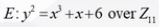
的k个点的和同样也满足这个方程,这是椭圆密码的前提。
例如,这个方程上的点两个(2,7)相加
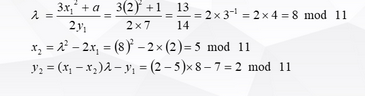
得到的点是(5,2),同样满足方程。
进一步,我们一直累加这个点,就可以逐渐得到所有满足方程的点

那么最后我们就进入到椭圆曲线密码学了
我们将ECC中的加法运算与RSA中的模乘运算对应,将ECC中的乘法运算与RSA的模幂运算对应,要建立基于椭圆曲线的密码体制,需要类似因子分解两个素数之积或求离散对数这样的难题。
考虑方程Q=kP,其中Q,P给给定曲线上的点,对给定的k,P计算Q比较容易,而对给定的Q和P计算k则比较困难,这就是椭圆密码的形成机制。实际应用中k的值非常大,从而使穷举攻击方法不可行。
下面举例与椭圆曲线形成的私钥和公钥
用椭圆曲线面貌实现Diffie-Hellman的交换
两个用户A和B
(1)选择Eq(a,b)(素曲线方程)和一个基点G(x,y)(阶为n),这两个是全局公开量
(2)用户A闲杂一个小于n的整数n1作为私钥,然后产生公钥p1=n1G;改公钥是E中的一个点
(3)用户B可累死的选择私钥n2并计算公钥p2
(4)A产生秘密钥K=n1p2,B产生秘密要K=n2*p1
容易证明,两个人的K是相同的
要破译这种体制,攻击者必须由G和kG计算k,这被认为是非常难的
椭圆曲线加解密
(1)将要发送的明文信息编码为形式(x,y)的点Pm,具体编码过程这里不讲了。。。
(2)每个用户A选择一个私钥n1,产生公钥p1=n1*G
(3)若A要将消息Pm加密后发送给B,则A随机选择1个正整数k,并产生密文Cm,该密文是一个点对
Cm={kG,Pm+kp2}
p2是B的公钥,B要对密文进行解密,则需要用第二个点减去第一个点与B的私钥之积
Pm+kp2-n2(kG)=Pm
例:


这一段 我知道很难理解,所以需要多看几遍还能慢慢有所体会。
