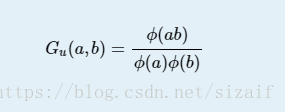@HDU多校训练7-1005@HDU6390 GuGuFishtion (欧拉函数 + 容斥|莫比乌斯)

版权声明：岂曰无衣,与子同袍 https://blog.csdn.net/sizaif/article/details/81736640

GuGuFishtion

Time Limit: 3000/1500 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1197    Accepted Submission(s): 454

 

Problem Description

Today XianYu is too busy with his homework, but the boring GuGu is still disturbing him!!!!!!
At the break time, an evil idea arises in XianYu's mind.
‘Come on, you xxxxxxx little guy.’
‘I will give you a function ϕ(x) which counts the positive integers up to x that are relatively prime to x.’
‘And now I give you a fishtion, which named GuGu Fishtion, in memory of a great guy named XianYu and a disturbing and pitiful guy GuGu who will be cooked without solving my problem in 5 hours.’
‘The given fishtion is defined as follow:

And now you, the xxxxxxx little guy, have to solve the problem below given m,n,p.’

So SMART and KINDHEARTED you are, so could you please help GuGu to solve this problem?
‘GU GU!’ GuGu thanks.

Input

Input contains an integer T indicating the number of cases, followed by T lines. Each line contains three integers m,n,p as described above.
1≤T≤3
1≤m,n≤1,000,000
max(m,n)<p≤1,000,000,007
And given p is a prime.

 

Output

Please output exactly T lines and each line contains only one integer representing the answer.

Sample Input

1 5 7 23

Sample Output

2

Source

[题意]:  很明确  求 

[思路]  根据 欧拉函数的性质   

   

然后可以化简   

成 求 

具体推导 : (参考的  (●'◡'●).jpg ) 

一个数肯定能表示成若干个质数的乘积，因此，设。

  (其余的项上下展开后都可以约掉，因为它们互质)

////////////////////////////////////////

然后:

提前预处理下 phi 欧拉表,

然后变成求  a-b  中  gcd 为 i 的 有序对个数 

[代码]

#include <iostream>
#include <bits/stdc++.h>

#define rep(i,a,n) for(int i =a ;i<=n;i++)
#define per(i,a,n) for(int i =n ;i>=a;i--)


typedef long long ll;
const int maxn = 1e6+10;



using namespace std;

int phi[maxn+10];
ll mod;
ll inv[maxn+10];
ll f[maxn];
void init()
{
    memset(phi,0,sizeof(phi));
    phi[1] = 1;
    for(int i = 2 ; i < maxn;i++)
    {
        if(!phi[i])
            for(int j = i ; j < maxn; j += i){
                if(!phi[j]) phi[j] = j;
                phi[j] = phi[j]/i*(i-1);
            }
    }

}

int main()
{
    init();
    int T;
    scanf("%d",&T);
    while(T--)
    {
        ll n,m;
        scanf("%lld %lld %lld",&n,&m,&mod);
        ll mn = min(n,m);
        inv[1] = 1;
        ll ans = 0;
        for(int i = 2 ;i < mn ; i++) inv[i] = (mod-mod/i)*inv[mod%i]%mod;
        memset(f,0,sizeof(f));
        for(int i = mn;i >=1 ;i--)
        {
            f[i] = 1ll*(n/i)*(m/i)%mod;
            for(int j = i+i; j <= mn;j+=i)
            {
                f[i] -= f[j];
                if(f[i] < 0) f[i] +=mod;
            }
            ans += i*inv[phi[i]]%mod * f[i]%mod;
            ans %=mod;
        }
        printf("%lld\n",ans%mod);
    }
    return 0;
}