HDU 6390 GuGuFishtion (莫比乌斯反演)

GuGuFishtion

Time Limit: 3000/1500 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1008 Accepted Submission(s): 377

Problem Description
Today XianYu is too busy with his homework, but the boring GuGu is still disturbing him!!!!!!
At the break time, an evil idea arises in XianYu’s mind.
‘Come on, you xxxxxxx little guy.’
‘I will give you a function ϕ(x) which counts the positive integers up to x that are relatively prime to x.’
‘And now I give you a fishtion, which named GuGu Fishtion, in memory of a great guy named XianYu and a disturbing and pitiful guy GuGu who will be cooked without solving my problem in 5 hours.’
‘The given fishtion is defined as follow:
$Gu(a,b)=\frac{ϕ(ab)}{ϕ(a)ϕ(b)}$

And now you, the xxxxxxx little guy, have to solve the problem below given m,n,p.’

$$(\sum_{a=1}^m\sum_{b=1}^nGu(a,b))(modp)$$

So SMART and KINDHEARTED you are, so could you please help GuGu to solve this problem?
‘GU GU!’ GuGu thanks.

Input
Input contains an integer T indicating the number of cases, followed by T lines. Each line contains three integers m,n,p as described above.
1≤T≤3
1≤m,n≤1,000,000
max(m,n)

思路

首先我们对$Gu(a,b)=\frac{ϕ(ab)}{ϕ(a)ϕ(b)}$化简一下我们知道$\phi(x)=x(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})$，$p_i$为不同的质数
所以就有$\phi(ab)=ab(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})$

$\phi(a)\phi(b)=ab(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_{k^{'}}})$

$ab$可以直接约掉，那么也就是说$\frac{\phi(ab)}{\phi(a)\phi(b)}=\frac{1}{(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})}$

分母的含义是，a，b中共同出现过的不同质数，我们有知道根据唯一分解定理

$a=p_1^{\alpha _1}p_2^{\alpha _2}\cdots p_k^{\alpha _k}$，$b=p_1^{\beta _1}p_2^{\beta _2}\cdots p_k^{\beta _k}$

而$gcd(a,b)=p_1^{min(\alpha _1,\beta _1)}p_2^{min(\alpha _2,\beta _2)}\cdots p_k^{min(\alpha _k,\beta _k)}$，其中有贡献的$p_i$就是a和b中都有出现的部分，而没出现的部分就是$p_i$为0，出现的次数也为0,$0^0=1$不影响，也就是$gcd(a,b)$其实和分母有些联系，在想想就会发现一些东西比如
$\phi(gcd(a,b))=gcd(a,b)(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})$，这里的$p_i$是在a，b中都有出现的部分，所以原式就可以变成

$$\frac{\phi(ab)}{\phi(a)\phi(b)}=\frac{gcd(a,b)}{\phi(gcd(a,b))}$$

那就有

$$\sum_{a=1}^m\sum_{b=1}^nGu(a,b)=\sum_{a=1}^m\sum_{b=1}^n\frac{gcd(a,b)}{\phi(gcd(a,b))}$$
而 $gcd(a,b)$每次都是有范围的， $1\sim min(n,m)$，所以我们可以尝试枚举 $gcd(a,b)$，即
$$ans=\sum_{d=1}^{min(n,m)}\sum_{a=1}^m\sum_{b=1}^n\frac{d}{\phi(d)}[gcd(a,b)==d]$$
$[gcd(a,b)==d]$即 $gcd(a,b)==d$为1，反之为0，那我们把 $\frac{d}{\phi(d)}$提前，即

$$ans=\sum_{d=1}^{min(n,m)}\frac{d}{\phi(d)}\sum_{a=1}^m\sum_{b=1}^n[gcd(a,b)==d]$$
$$\sum_{a=1}^m\sum_{b=1}^n[gcd(a,b)==d]$$ 就是单纯的莫比乌斯反演可以实现了
我们用莫比乌斯反演的倍数形式


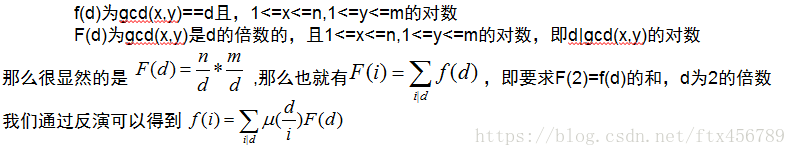
我们每次让 $n/d$和 $m/d$后问题就会转化为求解
$$\sum_{a=1}^{\frac{m}{k}}\sum_{b=1}^{\frac{n}{k}}[gcd(a,b)==1]$$

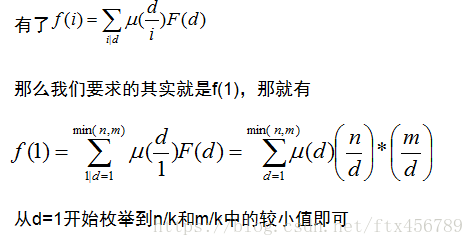
最后的我们求得莫比乌斯的函数是 $g(a,b)$
那么最后答案就是
$$ans=\sum_{d=1}^{min(n,m)}\frac{d}{\phi(d)}g(\frac{n}{d},\frac{m}{d})$$
我们预处理出 $\frac{d}{\phi(d)}$，这里还得用逆元逆处理一下，所以一共打三个表，一个是逆元的表一个是默比乌斯函数的表，一个是欧拉函数的表即可，求莫比乌斯还可以用 分块前缀和加速

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <math.h>
using namespace std;
const int N=1000005;
int p;
int vis[N];
long long mu[N];
long long prime[N];
long long inv[N];
long long sum[N];
long long a[N];
long long f[N];
long long euler[N];
int cnt;
void phi()
{
    for(int i=1; i<N; i++)
        euler[i]=i;
    for(int i=2; i<N; i+=2)
        euler[i]/=2;
    for(int i=3; i<N; i+=2)
    {
        if(euler[i]==i)
        {
            for(int j=i; j<N; j+=i)
            {
                euler[j]=euler[j]-euler[j]/i;
            }
        }
    }
}
void Init()
{
    memset(vis,0,sizeof(vis));
    mu[1] = 1;
    cnt = 0;
    for(int i=2; i<N; i++)
    {
        if(!vis[i])
        {
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for(int j=0; j<cnt&&i*prime[j]<N; j++)
        {
            vis[i*prime[j]] = 1;
            if(i%prime[j]) mu[i*prime[j]] = -mu[i];
            else
            {
                mu[i*prime[j]] = 0;
                break;
            }
        }
    }
    for(int i=1; i<N; i++)
        sum[i]=sum[i-1]+mu[i];
}
long long get(int n,int m)
{
    long long ans=0;
    for(int i=1,last; i<=min(n,m); i=last+1)
    {
        last=min(n/(n/i),m/(m/i));
        ans+=(sum[last]-sum[i-1])*(n/i)*(m/i);
        ans=(ans+p)%p;
    }
    return ans;
}
void ni(int n,int m)
{
    inv[1]=1;
    for(int i=2; i<=min(n,m); i++) inv[i]=inv[p%i]*(p-p/i)%p;
    for(int i=1; i<=min(n,m); i++)
    {
        a[i]=(long long)i*inv[euler[i]]%p;
    }
}
int main()
{
    Init();
    phi();
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,m;
        scanf("%d%d%d",&n,&m,&p);
        ni(n,m);
        long long ans=0;
        for(int i=1;i<=min(n,m);i++)
        {
            ans+=a[i]*get(n/i,m/i);
            ans%=p;
        }
        printf("%lld\n",ans);
    }
    return 0;
}