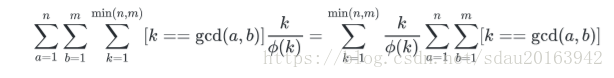（HDU6390）2018 Multi-University Training Contest 7 - 1005 - GuGuFishtion - 欧拉函数

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6390

题意：Gu(a,b)=phi(a*b)/(phi(a)*phi(b))，给出n，m，p求(∑a=1 to m ∑b=1 to n  Gu(a,b)) (modp)；

解析：来自dls直播

• 首先欧拉函数求解公式如下：
• 考虑a和b中的某个质因子p，假设p在a中有p^a1、p在b中有p^b1、p在a*b中有p^(a1+b1)；
• 若a1!=0&&b1!=0，则p对phi(a)的贡献是(p-1)*p^(a1-1)，p对phi(b)的贡献是(p-1)*p^(b1-1)，p对phi(a*b)的贡献是(p-1)^2*p^(a1+b1-2)；那么p对phi(a*b)/(phi(a)*phi(b))的贡献是p/(p-1)；
• 若a1=0，则p对phi(a*b)的贡献是(p-1)*p^(b1-1)，p对phi(a)*phi(b)的贡献也是(p-1)*p^(b1-1)，可得phi(a*b)/(phi(a)*phi(b))=1；b1=0时同理。
• 那phi(a*b)/(phi(a)*phi(b))=∏pk/(pk-1)=gcd(a,b)/phi(gcd(a,b))；
• 证：考虑∏pk/(pk-1)时，①.因为分子为a与b所有公共质因子p的乘积=gcd(a,b)；②.而分母为所有(p-1)的乘积，p为素数时phi(p)=p-1，而欧拉函数为极性函数，当n,m互素时，phi(n,m)=phi(n)*phi(m)；所以分母为phi(gcd(a,b))；

所以问题转化为证明：

• 这里设辅助函数f[i]表示d|gcd（a，b）的对数；
•                      设g[i]表示d=gcd（a，b）的对数；
• 那么容斥一下 f(d)=(n/d)*(m/d)；
•                       g(d)=f(d) - sum(g(k*d) 当k>=2);

g[i]就是 ∑a=1 to m ∑b=1 to n  [k==gcd(a,b)] 的a,b的对数。

代码：

//dls代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const ll N=1000000;
int pr[N/5],p[N+100],tot,phi[N+100];
ll f[N+10],inv[N+10];//f[i]=count(d|(a,b)),inv[i]是i的逆元
int n,m,mod;

ll gcd(ll a,ll b)
{
    return b?gcd(b,a%b):a;
}

void init()//欧拉函数打表
{
    phi[1]=1;
    p[1]=1;
    for(int i=2;i<N+1;i++)
    {
        if (!p[i])
        {
            p[i]=i;pr[++tot]=i;phi[i]=p[i]-1;
        }
        for (int j=1; j<=tot&&pr[j]*i<=N; j++)
        {
            p[i*pr[j]]=pr[j];
            if (p[i]==pr[j])
            {
                phi[i*pr[j]]=phi[i]*pr[j];
                break;
            }
            else phi[i*pr[j]]=phi[i]*(pr[j]-1);
        }
    }
    return;
}

int main()
{
    init();
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d",&n,&m,&mod);
        if (n>m) swap(n,m);
        inv[1]=1;
        for (int i=2; i<=n; i++)
            inv[i]=(mod-mod/i)*inv[mod%i]%mod;
        ll ans=0;
        for (int i=n; i>=1; i--)//这里n=min(n,m)
        {
            f[i]=(ll)(n/i)*(m/i);
            for (int j=i+i; j<=n; j+=i)
                f[i]=f[i]-f[j];
            ans=(ans+f[i]%mod*i%mod*inv[phi[i]])%mod;
        }
        printf("%I64d\n",ans);
    }
    return 0;
}