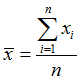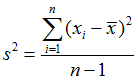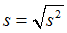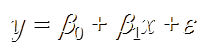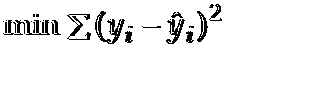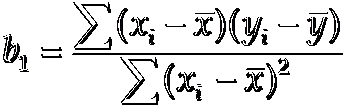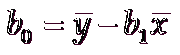0. 前提介绍:
为什么需要统计量?
统计量:描述数据特征
0.1 集中趋势衡量
0.1.1均值(平均数,平均值)(mean)
{6, 2, 9, 1, 2}
(6 + 2 + 9 + 1 + 2) / 5 = 20 / 5 = 4
0.1.2中位数 (median):
将数据中的各个数值按照大小顺序排列,居于中间位置的变量
给数据排序:1, 2, 2, 6, 9
找出位置处于中间的变量:2
当n为基数的时候:直接取位置处于中间的变量
当n为偶数的时候,取中间两个量的平均值
0.1.3众数 (mode):
数据中出现次数最多的数
0.2 离散程度衡量
0.2.1 方差(variance)
{6, 2, 9, 1, 2}
(1) (6 - 4)^2 + (2 - 4) ^2 + (9 - 4)^2 + (1 - 4)^2 + (2 - 4)^2
= 4 + 4 + 25 + 9 + 4
= 46
(2) n - 1 = 5 - 1 = 4
(3) 46 / 4 = 11.5
0.2.2 标准差 (standard deviation)
s = sqrt(11.5) = 3.39
1. 介绍:
回归(regression):Y变量为连续数值型(continuous numerical variable)
如:房价,人数,降雨量
分类(Classification):Y变量为类别型(categorical variable)
如:颜色类别,电脑品牌,有无信誉
2. 简单线性回归(Simple Linear Regression)
2.1 很多做决定的过程通常是根据两个或者多个变量之间的关系
2.2 回归分析(regression analysis):用来建立方程模拟两个或者多个变量之间如何关联
2.3 被预测的变量叫做:因变量(dependent variable), y, 输出(output)
2.4 被用来进行预测的变量叫做: 自变量(independent variable), x, 输入(input)
3. 简单线性回归介绍
3.1 简单线性回归包含一个自变量(x)和一个因变量(y)
3.2 以上两个变量的关系用一条直线来模拟
3.3 如果包含两个以上的自变量,则称作多元回归分析(multiple regression)
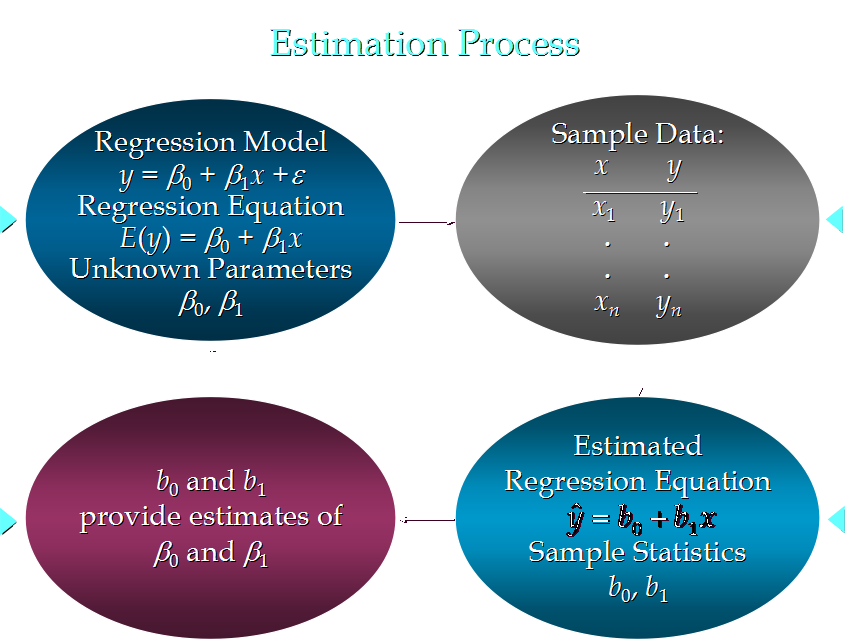
4. 简单线性回归模型
4.1 被用来描述因变量(y)和自变量(X)以及偏差(error)之间关系的方程叫做回归模型
4.2 简单线性回归的模型是:
其中:β0与β1被称为参数, ε被称为偏差
5. 简单线性回归方程
对回归模型两边求期望,得到:
E(y) = β0+β1x
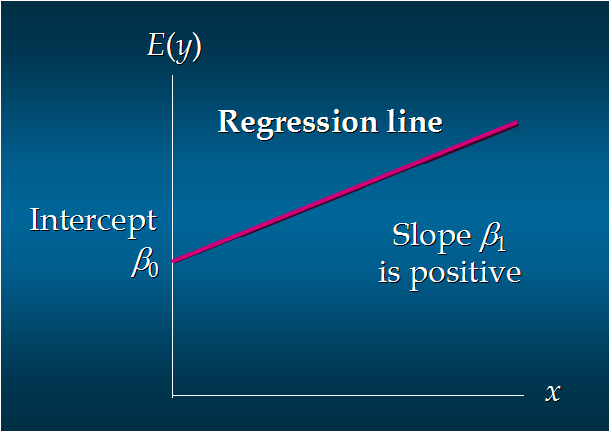
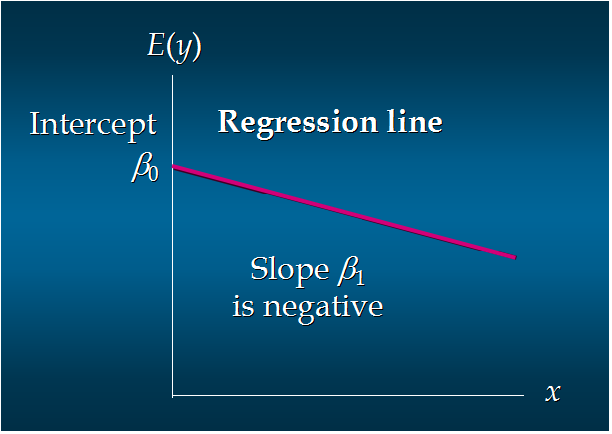
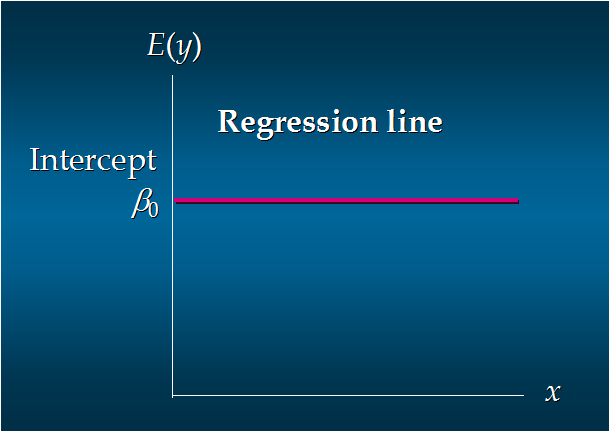
这个方程对应的图像是一条直线,称作回归线。其中,β0是回归线的截距,β1是回归线的斜率。E(y)是在一个给定x值下y的期望值(均值)。
6. 正向线性关系:
7. 负向线性关系:
8. 无关系:
9. 估计的简单线性回归方程
ŷ=b0+b1x
这个方程叫做估计线性方程(estimated regression line)
其中,b0是估计线性方程的纵截距,b1是估计线性方程的斜率,ŷ是在自变量x等于一个给定值的时候,y的估计值。
10. 线性回归分析流程:
11. 关于偏差ε的假定
11.1 ε是一个随机的变量,均值为0
11.2 ε的方差(variance)对于所有的自变量x是一样的
11.3 ε的值是独立的
11.4 ε满足正态分布
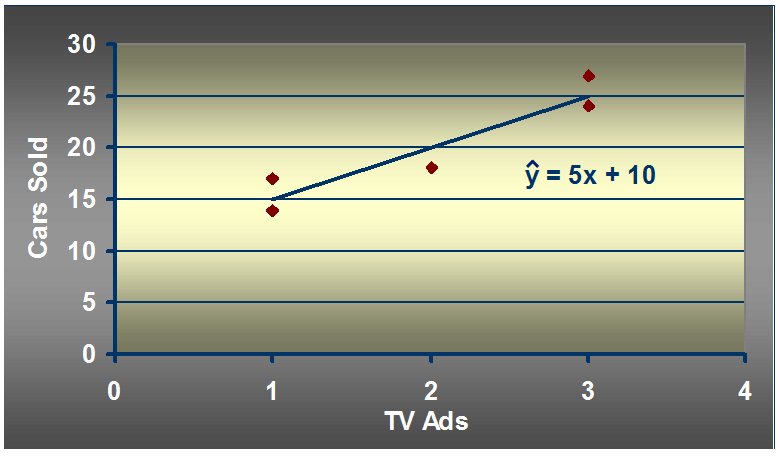
12. 简单线性回归模型举例:
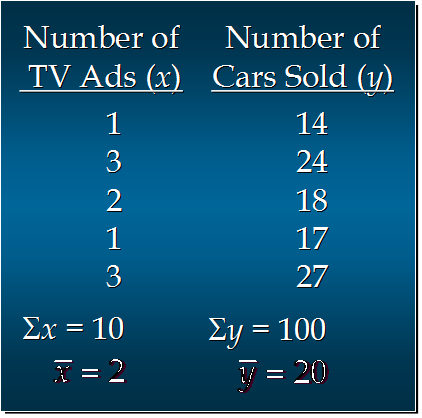
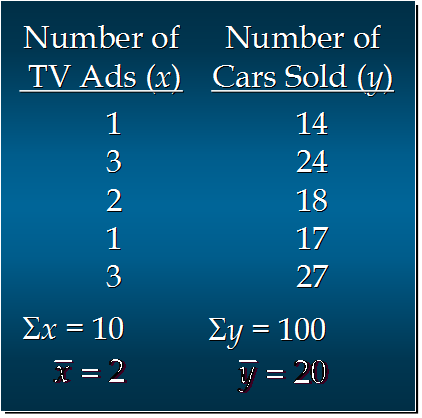
汽车卖家做电视广告数量与卖出的汽车数量:
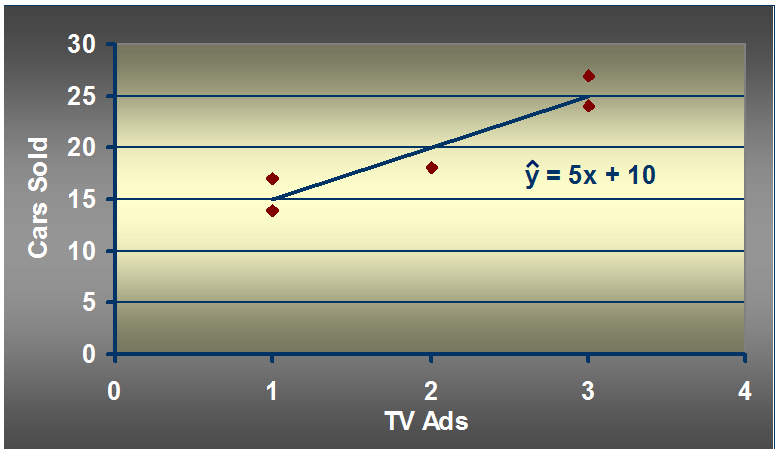
12.1 如何画出适合简单线性回归模型的最佳回归线?
使sum of squares最小
计算过程
分子 = (1-2)(14-20)+(3-2)(24-20)+(2-2)(18-20)+(1-2)(17-20)+(3-2)(27-20)
= 6 + 4 + 0 + 3 + 7
= 20
分母 = (1-2)^2 + (3-2)^2 + (2-2)^2 + (1-2)^2 + (3-2)^2
= 1 + 1 + 0 + 1 + 1
= 4
b1 = 20/4 =5
b0 = 20 - 5*2 = 20 - 10 = 10
12.2 预测:
假设有一周广告数量为6,预测的汽车销售量是多少?
x_given = 6
Y_hat = 5*6 + 10 = 40
12.3 Python实现:
测试代码:
#coding:utf-8
#一元线性回归实例
#模型函数:y = b0 + b1*x
import numpy as np
#定义简单线性回归函数,求b0和b1
def fitSLR(x,y):#输入参数(x1,x2,x3...xn),(y1,y2,y3...yn)
n = len(x)
dinominator = 0#分子
numerater = 0#分母
for i in range(0,n):
numerater += (x[i] - np.mean(x))*(y[i] - np.mean(y))
dinominator += (x[i] - np.mean(x))**2
b1 = numerater/float(dinominator)
b0 = np.mean(y) - b1*np.mean(x)
return b0,b1
#求y值
def predict(x,b0,b1):
return b0 + b1*x
#main函数
if __name__ == "__main__":
x = [1,3,2,1,3]
y = [14,24,18,17,27]
b0,b1 = fitSLR(x,y)
print("b0 = ",b0)
print("b1 = ", b1)
x_test = 6
y_hat = predict(x_test,b0,b1)
print(u"y的预测值:",y_hat)
输出:
('b0 = ', 10.0)
('b1 = ', 5.0)
(u'y的预测值:', 40.0)