概率论与统计：条件期望与最小二乘法

文章向导

条件期望
最小二乘法
探索平方误差的期望值内涵

一、条件期望

　　条件期望在概率论与统计中也被称为条件数学期望，它的用途主要是用于实际的预测性问题。如对于两个互有影响的随机变量，如果我们知道其中一个随机变量X=a这一观测值，要据此去估计或预测随机变量Y的取值。
　　首先，想到的自然是选择条件概率P(Y=b|X=a)值最大时的b作为答案，如果需要尽可能地提高估计的精度，那么此方法无疑是很合理的。
　　另一种做法做法则是求在X=a时Y的条件分布，并计算出相应的期望值，即：

$$E\left( Y|X=a \right) \equiv \,\,\sum_b{b}P\left( Y=b|X=a \right) 　　（1-1）$$

　　上式也就是条件期望的定义式。但需要注意到，对于取值不同的X，其条件期望E(Y|X=a)的值也不同。所以，如果能知道X各种取值出现的概率，那么条件期望的最终计算结果则与一般的期望值E(Y)一致，即：

$$E\left( Y \right) =\sum_a{E\left( Y|X=a \right) P\left( X=a \right)}　　（1-2）$$
　　现在来详细证明式(1-2)是如何得出的，先将式(1-1)代入进行推导。

---

二、最小二乘法

1.实例推导

　　接下来这部分，则是与条件期望相关的一个应用实例。我们先思考如下问题，假设有条件分布$P(Y=b|X=a)$，试设计一个程序，如何使得在输入X之后输出Y的估计值$\hat{Y}$。并使平方误差$\left( Y-\hat{Y} \right) ^2$的期望值$E\left[ \left( Y-\hat{Y} \right) ^2 \right]$ 尽可能小。
　　乍一看问题貌似很复杂，实际上要求的就是输入X后输出Y的估计值函数中，使$E\left[ \left( Y-\hat{Y} \right) ^2 \right]$ 的值最小时所对应的那个$\hat{Y}=g\left( X \right)=E(Y|X=x)$。再具体一点，其实问题的答案就是之前所谈及的条件期望g(a)=E(Y|X=a)。这点也符合人们的直观理解，估计值$\hat{Y}$与Y十分接近时，平方误差自然小。
　　为了简化问题的分析，可将X的取值范围给固定为{1,2,3}，此时平方误差的期望值如下所示。

　　上图中最后一行等式可分为3个部分，取决于g(1)的量+即取决于g(2)的量+即取决于g(3)的量。那么，现在的问题就转化为求各部分的解，然后则能得出最佳的g。即定义g(1)，使$\sum_b{\left( b-g\left( 1 \right) \right) ^2P\left( X=\text{1,}Y=b \right)}$有最小值，同理g(2)和g(3)类似。
　　接着，根据上述的思路来找出这样的g(1)，为表示方便用$g_1$替代g(1)。

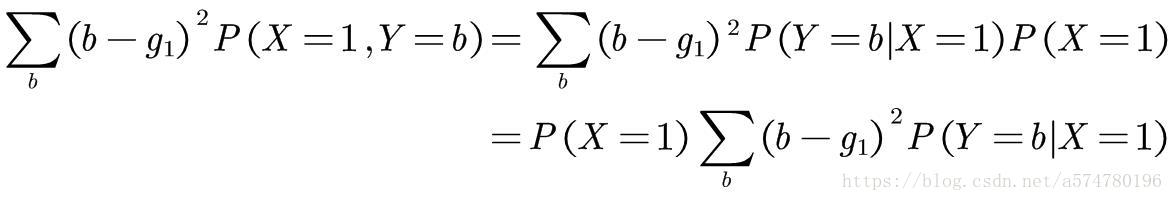
　　求该式的最小值等价于求$h_1(g_1)=\sum_b{\left( b-g_1 \right) ^2P\left( Y=b|X=1 \right)}$的最小值。好，马上就要成功了，让我们来计算它的微分。

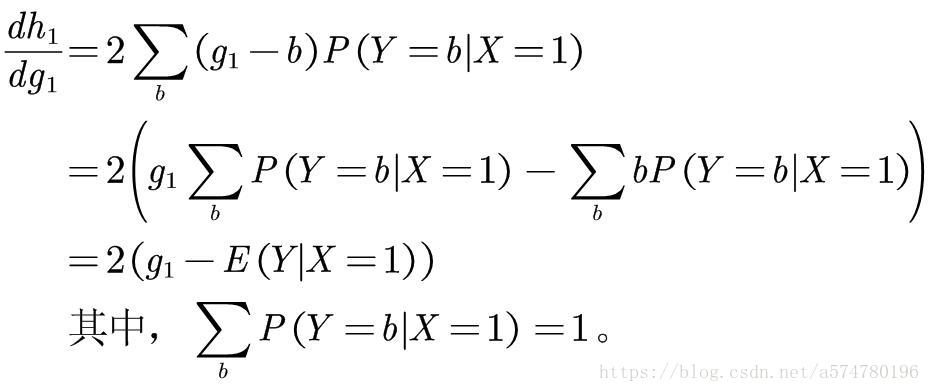
　　由极值的判定关系可知，当$dh_1/dg_1=0$时，即$g_1=E(Y|X=1)$时，$h_1(g_1)$能取到最小值，$h_2(g_2)$、$h_3(g_3)$同理可得。最后，从而推得$g(a)=E(Y|X=a)$的结论。

---

2.如何理解所求得的g(a)？

　　从$g(a)=E(Y|X=a)$形式上来看，它就是一个普通的函数。只要提供一个具体的数值a，它就会返回一个确定的值g(a)。那么，如果给g提供一个随机变量X，就能得到一个与X对应的随机变量$\hat{Y}=g(X)=E(Y|X=x)$。好吧，表达式看起来依然是那么的抽象。

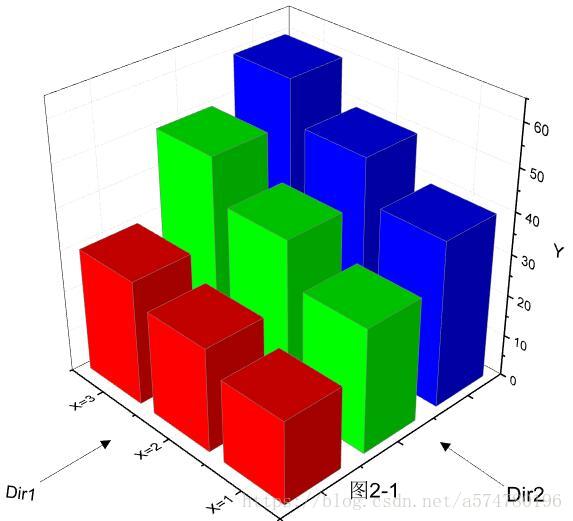
　　不妨看看图2-1，X=1,2,3分别对应着前面所提及的三个部分，可以把这三个部分想象为各自独立的平行世界，每个平行世界的Y值(柱状体的高)不尽相同(Dir2方向观察)，且同一平行世界下的Y值也不等(Dir1方向观察)。可能有些读者会迷惑，为啥同一平行世界下的Y值也不相同，那么请思考下条件分布P(Y|X=1)。

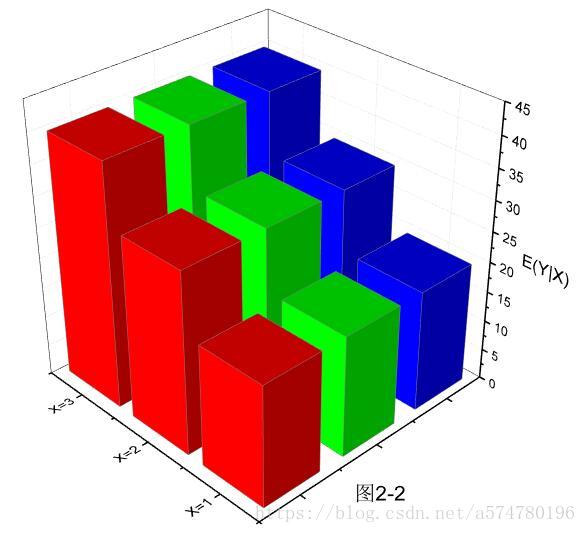
　　接着看图2-2，此时柱状体的高为E(Y|X)的值，而且有趣的是同一平行世界下的高现在是相等的。这点很好理解，因为求的是期望，那么最终结果肯定是将同一X区域下的不同高度给统一起来(也就是平均效果)。若是将三个平行世界的结果再继续综合起来，则最终得到E(Y)。
　　

---

三、探索平方误差的期望值内涵

1. 从偏差的平方到方差

　　谈及平方误差，读者的第一反应或许会是方差。那么，让我们先从方差开始谈起。设随机变量X的数学期望$E\left( X \right) =\mu$，现在我们需要计算它的实际取值$x与\mu$的差距。$|x-\mu |$可能是最为直观的方式，但落实到具体的计算时，绝对值的存在往往会带来许多不便(如分类讨论、曲线折角处不可微等)。于是，人们通常用偏差的平方$\left( x-\mu \right) ^2$来描述问题。
　　这样的描述也非常符合离散程度的定义，因为仅当$X=\mu$时，误差为0，其余情况误差总是存在且大于0。目前离方差的定义$V\left[ X \right] =E\left[ \left( X-\mu \right) ^2 \right]$很接近了，但还差一个取期望。Ok，思考下为何还要取一个期望才能得到方差？首先，$\left( X-\mu \right) ^2$得到的是一个随机值，而我们希望得到的是一种数值固定的指标，固取其期望来消除其中的随机性。

2.平方误差的期望值

　　正式往下说之前，读者应该现了解这个公式$V\left[ X \right] =E\left( X^2 \right) -E\left( X \right) ^2$。
　 试证：对于常量a，当$E\left( X \right) =\mu \text{，}V\left( X \right) =\sigma ^2$时，有等式$E\left[ \left( X-a \right) ^2 \right] =\left( \mu -a \right) ^2+\sigma ^2$成立。

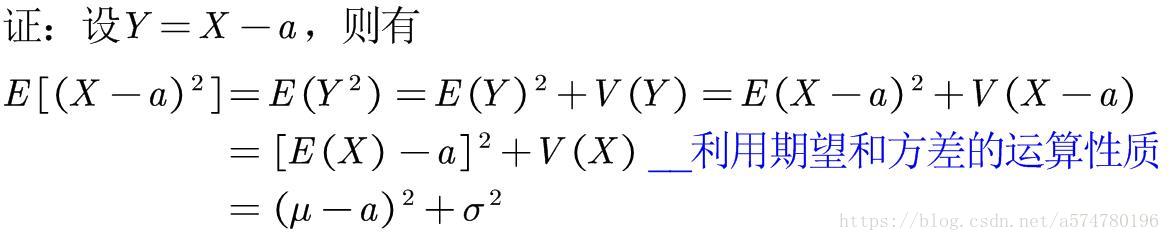
　　证明完毕，现在来说道说道如何理解这个等式。假设某工厂要生产尺寸恰好为a cm的零件，而最终实际产品的尺寸为X cm。那么，现在$\left( X-a \right) ^2$就为平方误差。与上述证明的等式相比较，可发现该误差被分解为如下两种误差：(期望值的平方误差)+方差 =（由偏移引起的误差）+（由离散引起的误差）。
　　更为专业的说法则是，系统误差(又称偏性误差，数值整体偏移)与随机误差(又称机会误差，数值离散)。
　　那么，由于生产工艺的不同，最终得到的产品在两种误差上的表现也会不同。如系统误差较小，随机误差较大。虽然看似误差较小，但其实数值X较为离散。

参阅资料
程序员的数学<概率统计>
概率论与数理统计<浙大版>