“””
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数,小数部分将被舍去。
Implement int sqrt(int x).
Compute and return the square root of x.
“””
我们要求
就是求
的解,且x为非负数。
解决Sqrt求平方根可以采取牛顿迭代法,下面简单介绍一下牛顿迭代法,更多的可以自己搜搜。
在曲线上随便找一个的A点,(事先不知道根点就是解在那儿,所以随便找一个点),做一个切线,切线的根(就是和x轴的交点)与曲线的根,存在一定的距离。可以从这个切线的根出发,做一根垂线,和曲线相交于B点,继续重复刚才的工作:可以发现
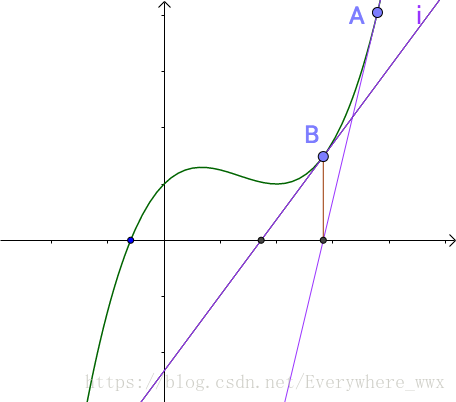
B点比之前A点更接近曲线的根点。那么经过多次迭代后会越来越接近曲线的根。
已知曲线方程
,在
点做切线,求
:
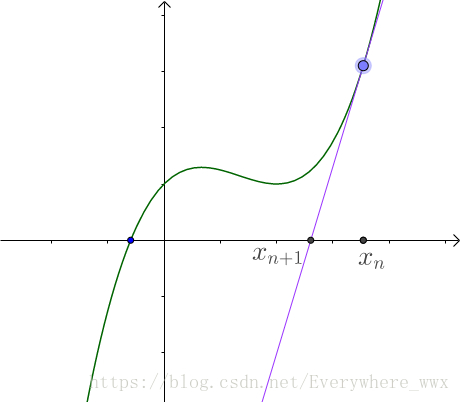
点的切线方程为:
。
要求
,就求
的解。
可以得到
;
我们将
代入到
中,可以得到一个比
更接近与方程的根点(解),多次迭代就可以得到一个近似于
的
。 即
所以代码就如下所示
class Solution(object):
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
result = 1.0
while abs(result * result - x) > 0.1:
result = (result + x / result) / 2
return int(result)至于如何设计逼近的程度,取决于设置的精度。如0.1…..等。
但是如何确定B点就比A点更接近与根点。可以就这题而言,做差最简单。
就可以得出!
ps:这题虽然简单,但是确实让我好学了一把牛顿迭代法!