队列是一种先进先出(FIFO First In First Out)的数据结构,它类似于下面这幅图:
队列的进出方式类似于平时我们排队打饭,来排队的人从队尾进入,打完饭的人从队头弹出。
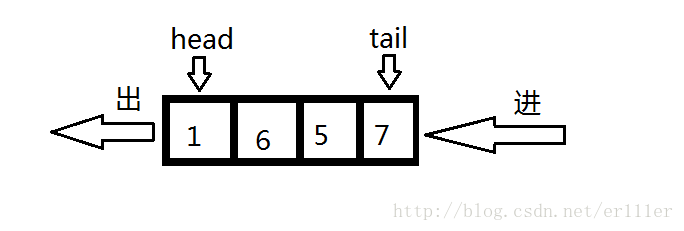
队列的在程序中储存的方式有很多,OI中最为常用的是使用头指针head和尾指针tail进行存储
头指针指向队列中第一个元素,尾指针指向队列中的最后一个元素,我们很显然可以得出队列进出的操作:
C++代码:
int que[100];
int head = 0, tail = 0;
//进队
void push(int a)
{
que[++tail] = a;
}
//出队
int pop()
{
return que[++head];
}
//判断队列是否为空
bool empty()
{
return !(head < tail);
}单调队列顾名思义就是一个有规律的队列,这个队列的规律是:所有在队列里的数都必须按递增(或递减)的顺序列队,如果真有这么一个队列,那么队列的头是不是就是最小(或最大)的呢?
当然队列的存储还有链表,以及循环队列等方式,读者可以自己在网上查找对应的讲解文章,这里不再叙述。
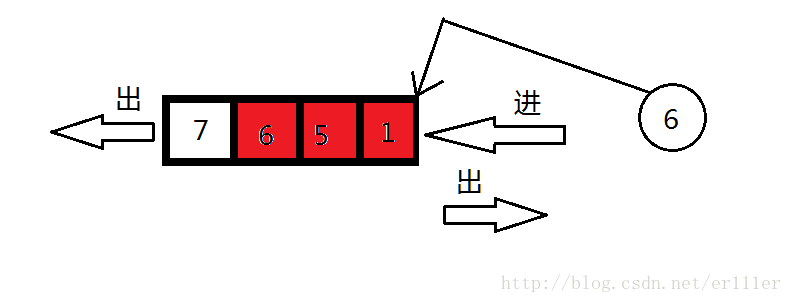
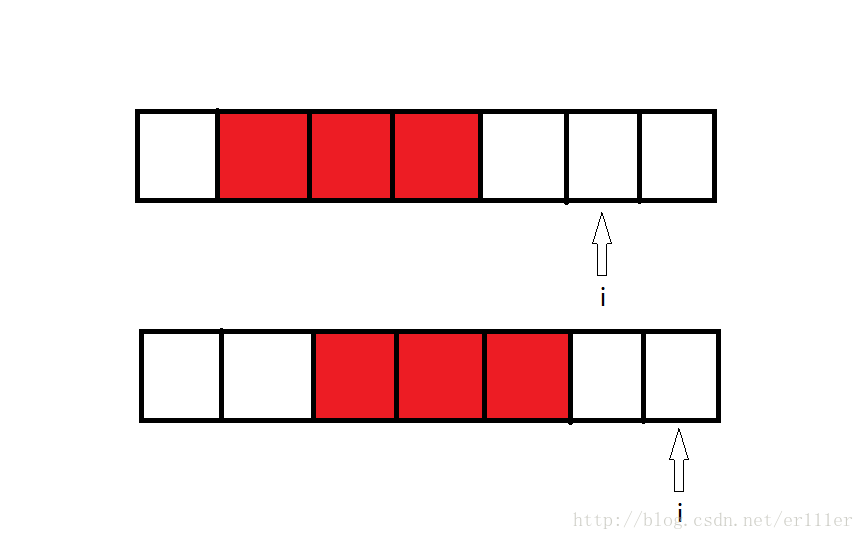
回到上面的单调队列问题,假如你在饭堂打饭时,有个人人高马大,急匆匆跑过来,看排了这么一长串队,心中急躁,从队列最后的一个人开始,看见好欺负的就赶走,自己站着,直到干不过的就停下,这就是双端队列。也就是允许两端弹出,只允许一端插入的队列(允许两端插入,只允许一端弹出的也属于双端队列)。这个人的插队行为类似于下面这幅图。
例题:(来源:caioj 1172)
给定一个n个数的数列,从左至右输出每个长度为m的数列段内的最大数。
解法1:
如果按照常规方法,我们在求f[i]即i~i+m-1区间内的最值时,要把区间内的所有数都访问一遍,时间复杂度约为O(nm)。有没有一个快一点的算法呢?
解法2:
我们知道,上一种算法有一个地方是重复比较了,就是在找当前的f(i)的时候,i的前面k-1个数其它在算f(i-1)的时候我们就比较过了。那么我们能不能保存上一次的结果呢?当然主要是i的前k-1个数中的最大值了。答案是可以,这就要用到单调递减队列。
使用单调队列就涉及到去头和删尾:
1、队列的头一定是在一段时间前就加入了队列,现在的队列头会不会离开了我们处理的区间呢?如果它离我们正在处理的i太远了,我们就要把它去掉,去除冗杂的信息。
2、为了保证队列的递减性,在从列队尾新插入元素v时,要考虑队列尾的值是否大于v,如果是,队列呈现 队列尾-1的值 > 队列尾的值 > v ,此时队列递减性没有消失;如果不是,队列呈现 队列尾-1的值 > 队列尾的值 < v ,队列递减性被打破。
为了维护递减性,我们做如下考虑:v是最新值,它的位置是目前最靠后的,它可成为以后的最大值,必须留下;队列尾-1的值与v大小不定,不能冒然删去它;队列尾的值夹在v和队列尾-1之间,它不但不是最大值,对于以后的情况又不如v优,因为v相比队列尾更靠后(v可以影响到后m个值,队列尾只能影响到从它的位置往后数m-1个值),而且值更大,所以删队列尾是必定的。
在维护好一个 区间正确、严格递减 的单调递减队列后,队列头就是当前区间的最大值了。
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int a[200000];
struct node
{
int x,p;
node(){}
node(int xx,int pp){x=xx;p=pp;}
}list[200000];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int head=1,tail=1;
list[1]=node(a[1],1);
for(int i=2;i<=n;i++)
{
while(head<=tail&&list[tail].x<=a[i]) tail--;//删尾
list[++tail]=node(a[i],i);//得到最优解并插入
while(i-list[head].p>=m) head++;//去头
if(i>=m) printf("%d\n",list[head]);
}
return 0;
}
烽火台又称烽燧,是重要的军事防御设施,一般建在险要或交通要道上。一旦有敌情发生,白天燃烧柴草,通过浓烟表达信息;夜晚燃烧干柴,以火光传递军情,在某两座城市之间有 n 个烽火台,每个烽火台发出信号都有一定代价。为了使情报准确地传递,在连续 m 个烽火台中至少要有一个发出信号。请计算总共最少花费多少代价,才能使敌军来袭之时,情报能在这两座城市之间准确传递。
Input
第一行:两个整数 N,M。其中N表示烽火台的个数, M 表示在连续 m 个烽火台中至少要有一个发出信号。接下来 N 行,每行一个数 Wi,表示第i个烽火台发出信号所需代价。
Output
一行,表示答案。
Sample Input
5 3
1
2
5
6
2Sample Output
4Data Constraint
对于50%的数据,M≤N≤1,000 。 对于100%的数据,M≤N≤100,000,Wi≤100。
分析题目,由于题目要求连续m个烽火台中至少要有一个发出信号,很容易得出DP转移方程:
F[i]=min(F[j]:i−m<j<i)+a[i]F[i]=min(F[j]:i−m<j<i)+a[i]
最直接的方法是枚举状态,对于每一个i,我们在i-m+1到i-1中寻找一个最小的F[j]进行状态转移,枚举状态的时间复杂度是O(n),寻找最小值的状态时间复杂度是O(n),因此这种方法的复杂度是O(n^2)。题目的是数据范围是n<=100000,显然超时。
那么怎么用单调队列优化呢?
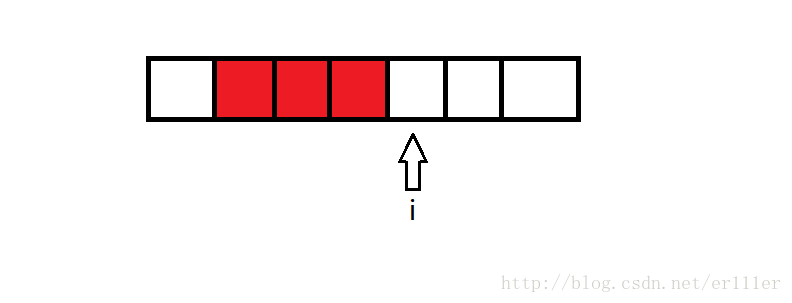
。上图中,状态枚举到i,当m=4时,我们要做的就是在i-3到i-1中找到最小的F[j],那么枚举到i+1时,我们要做的就是要在i-2到i中找到最小的F[j]。上图中我们可以看出,要寻找最小值的区间向后移动了一位,也就是F[i-m+1]的值被抛弃,F[i-1]的值被加入。这里就可以用单调队列处理了,F[i-1]是插队的数据,F[i-1]有资格插队是因为它更优且更靠近i,比它更差的数将被它取代,保留那些数据没有任何好处。而那些已经不再维护区间之外的就不必再对其进行维护,出队即可。看了代码会更加明白:
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100000;
int n, m, head = 1, tail = 0, ans = 2147483647;
int a[N + 1], f[N + 1], que[N + 1];
int main()
{
freopen("beacon.in", "r", stdin);
freopen("beacon.out", "w", stdout);
scanf("%d%d", &n, &m);
for (int i = 1;i <= n;i++)
scanf("%d", &a[i]);
for (int i = 1;i <= n;i++)
{
while (head <= tail && f[i - 1] <= f[que[tail]]) tail--; //当F[i-1]比队尾值更优时把队尾值弹出
que[++tail] = i - 1; //把F[i-1]插入,这里插入下标而不插入值,便于从队头弹出
while (head <= tail && que[head] < i - m) head++; //不属于区间维护内的数弹出
f[i] = f[que[head]] + a[i]; //状态转移
}
for (int i = n;i > n - m;i--) //求出答案
ans = min(ans, f[i]);
printf("%d\n", ans);
fclose(stdin);
fclose(stdout);
return 0;
}上题仅是单调队列最简单的应用,下面再给一道例题分析加深印象。
JZOJ 1772 假期
Description
经过几个月辛勤的工作,FJ决定让奶牛放假。假期可以在1…N天内任意选择一段(需要连续),每一天都有一个享受指数W。但是奶牛的要求非常苛刻,假期不能短于P天,否则奶牛不能得到足够的休息;假期也不能超过Q天,否则奶牛会玩的腻烦。FJ想知道奶牛们能获得的最大享受指数。
Input
第一行:N,P,Q.
第二行:N个数字,中间用一个空格隔开,每个数都在longint范围内。
Output
一个整数,奶牛们能获得的最大享受指数。
Sample Input
5 2 4
-9 -4 -3 8 -6
Sample Output
5
Data Constraint
50% 1≤N≤10000
100% 1≤N≤100000
1<=p<=q<=n
Hint
选择第3-4天,享受指数为-3+8=5。
看到区间的问题首先肯定是想到求前缀和,我们把[1,k]的和记为sum[k],可以得到sum[i] = sum[i - 1] + a[i],[l,r]的和即为sum[r] - sum[l - 1](这里视sum[0] = 0)。我们假设选择的区间为[l,r]且r固定,可知r−q+1≤l≤r−p+1r−q+1≤l≤r−p+1,若要使[l,r]区间的值最大,则sum[l - 1]需最小,才可使得sum[r] - sum[l - 1]最小,当i右移一位到i+1,因为p,q为给定不变的值,对应寻找最小sum[l-1]的区间也右移一位,与上题同。
如下图,当p=3,q=5时:
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
int n,p,q,l,r,head = 1,tail = 0,ans = -2147483647;
int que[100001],a[100001];
long long sum[100001];
int max(long long a,long long b)
{
return a > b ? a : b;
}
int main()
{
sum[0] = 0;
scanf("%d %d %d", &n, &p, &q);
for (int i = 1;i <= n;i++)
{
scanf("%d", &a[i]);
sum[i] = sum[i-1] + a[i]; //记前缀和
}
for (r = p;r <= n;r++)
{
while (head <= tail && sum[que[tail]-1] >= sum[r-p]) tail--; //更优的sum[l - 1]予以插队
que[++tail] = r+1-p; //入队
while (head <= tail && que[head] < r+1-q) head++; //不处于维护范围内的出队
ans = max(ans, sum[r]-sum[que[head]-1]); //更新答案
}
printf("%d\n", ans);
return 0;
}关于单调队列的运用还有很多,例如斜率优化DP等等。总而言之,使用单调队列优化DP,那么必会有求i之前某个范围的极值的操作,这类DP的方程通常为:
F[i]=min(F[j]+a[i]:j<i)F[i]=min(F[j]+a[i]:j<i)
a[i]是与j无关的数。
优化无止境!