要看懂本篇的内容,首先需要对dfs序和lca的基础内容做一些了解(还有线段树= =),不清楚的读者欢迎看我之前写过的博客:http://blog.csdn.net/amuseir/article/details/79327624(dfs序)
http://blog.csdn.net/amuseir/article/details/79301619(线段树)
六种最基本操作为:
1、单点修改、子树查询。
2、子树修改、单点查询。
3、子树修改,子树查询。
4、单点修改、链查询。
5、链修改,子树查询。
6、链修改、链查询。
(当然,这些内容大多数都跟lca有关系,所以我上一次顺便也把lca一块儿讲了)在上一次讲树形结构基本操作的内容中,我们提到了关于一颗树形结构里面的一些常见操作,但当时的操作仅仅能够解决前五种问题(其实只能解决前四种,因为第五种操作稍微做一下修改这题就挂了。。。。真正上了考场怎么可能出这种裸题嘛= =)
那么我们今天就为大家介绍一种吊炸天的数据结构--树链剖分,它可以轻松解决以上的六种操作(当然,作为方便的代价,程序贼长而且容易写错QAQ)。
对于以上的六个问题,我们的常规式解决方法已经在上一篇博客里讲的很清楚了,但我们需要的是一种具有广泛性的特殊的数据结构,它能够尽可能的处理更多的问题(其实我说的就是树链剖分啦………………->_->)。
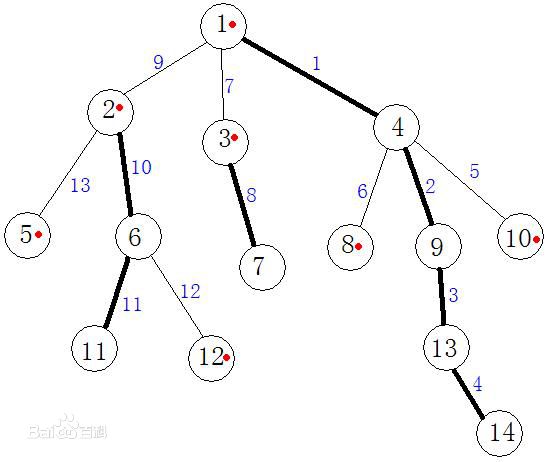
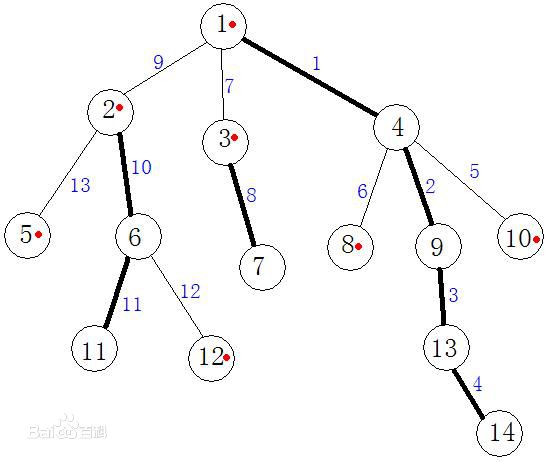
好的那么让我们来看到一颗任(biao)意(zhun)的树
好吧,说句实话,你在百度上的任何地方搜索树链剖分,搜出来的例题的图差不多都是这张(因为这张图实在是太经典了),那么在正式学习之前,我们首先需要搞清楚几个重要的概念。
重儿子:某个节点的子节点重大小最大的。
轻儿子:某个节点的子节点中除了重儿子以外其它的节点。
重链:链接节点和重儿子的边
轻边:除了重链以外的所有边。
所以说啊,链剖链剖,就是剖分重链和轻边啦。。。。
我们 那这张标准的经典图来举例子吧:
对于根节点1来说,它的三个儿子里面,2的大小是5,3的大小是2,4的大小是6,所以说点1的重儿子是6(当然,当一个点的多个儿子节点的大小一样的时候,随便取其中的一个就好啦^_^)
同理,我们可以发现图中所有的重儿子分别为:6(2的重儿子)、11(6的重儿子)、7(3的重儿子)、4(1的重儿子)、9(4的重儿子)、13(9的重儿子)、14(13的重儿子)。
然后,我们在进行dfs序的时候,把所有的重链上的所有点全部放在一起(先遍历重链),就可以摆出来一个非常神奇的结构(嗯……马上就知道为什么神奇了)
比如说对于这个标准图来说,树链剖分后的dfs序可以为:1 4 9 13 14 8 10 3 7 2 6 11 12 5。
所有的重链:1->4->9->13->14 ///2->6->11///3->7都被摆在了一起。
通过我之前讲dfs序的博客,我们可以首先发现,链剖过后的dfs序仍然满足最最最基本的性质:in[u]->out[u]是树某一个树和它的子树。
然后……它还满足一些其它的特殊性质……比如说链修改和链查询。
我们可以发现,修改/查询点12到点7的这整条链,就是修改点12->6->2->1->3->7 也可以看作是12->12这条链上的点(单点都是特殊的链)+6->2上的所有点+1->1+3->7,换句话说,我们修改的所有点都在重链和重链的深度最小的点的父亲上!
而正巧,我们在进行dfs的时候,就已经把重链分好了,所以说,我们就可以利用链剖形成的特殊dfs序来完成链修改和链查询。
值得一提的是,树链剖分也可以求lca(这是废话.......),时间复杂度与倍增求lca(就是之前那篇博客里详细描述的方法)一样,是O(log(n))的(然而实际操作起来,链剖的版本要简单易懂一些,而且真正计算的时候,我们会发现链剖的实现很多时候快于倍增);
在这张图中,我们如果要求11和6的lca该如何操作呢?我们先判定11和6是否在一条重链上,只要在的话,那就直接返回深度更小的那个点(比如在这里,就直接返回6)。
当然,如果两个点并不在一条重链上的话,就得进行正常的操作啦。。
我们在刚才求链修改方法的时候有提到过,我们会记录某一个点通过重链可以到达的深度最小的点(比如说11可以通过重链可以通过重链到达的深度最小的点就是2,而12可以通过重链到达的深度最小的点就是它自己)
而所有不在重链上的点,它们能够通过重链到达的深度最浅的点,都是它们自己(因为它们不在重链上。。。所以不能通过重链往上跳)
我们还会记录某一个点的父亲节点(仔细想一想原因,如果我们不记录这些点的话,会导致那些不在重链上的点,由于它们可以通过不管怎么修改,都只能修改到自己,没有办法实现跳步的操作),我们设top[u]是指u通过重链能够到达的深度最浅的点,用fat[u]吧,那么对于12这个点来说,top[12]=12,而fat[top[12]](等同于fat[12])为6。
这样我们就能大概总结出一个像样的思路:对于我们要寻找lca的两个点,我们先看是否在一条重链上,如果在的话,直接返回深度浅的那个点,如果不在的话,就把fat【top【某个点】】的深度小的那个点往上跳,跳到fat【这个点】之后,再用相同的方法来比较(如果你理解这段话是什么意思,就会发现实现起来轻松愉快好理解,而且比倍增求lca好写得多),知道两个点最终到达了一条重链上,这时候我们再返回深度浅的那个点,perfect。
我们发现,如果结合线段树的话,树链剖分过后形成的dfs序可以轻松愉快方便易懂得解决很多很多的问题,那么代价呢?(贼tm不好写,我们需要两次dfs,再加上线段树,最后的代码量还是有点大的,换句话说,如果用st表和倍增的话。。。。动了脑子,就可以少动一点手。。。但是链剖简单无脑,所以得多动手)
那么我们接下来看一看关于代码实现的操作(为了尽量避免有读者会忘记上文的内容,我会加上注释哒^_^)
首先是如果我们要搞出一个树链剖分的结构,需要哪些数组来作为支撑条件(剖分树的条件其实只有7个,但是我们要再用一个seq[]来存dfs序,所以就是8个)。
siz[u],用于计算u这个节点的大小(用于划分重链轻边)
fat[u],保存u节点的父亲节点。
son[u],u这个节点的重儿子是哪一个。
dep[u],u这个节点的深度。
这四个是在第一个dfs当中能够计算得到的条件(相当于我们要剖分一棵树的基本条件,可以看作是剖分的预处理)。
top[u],个人认为最重要的一个数组,保存一个点通过重链可以到达的深度最小的点。
seq[],保存dfs序后的节点。
in[u],某个节点进入seq[]时候的下标。
out[u],某个节点出dfs序时候的下标(关于dfs序在我的上一篇博客里讲的还算是比较清楚了吧,不清楚的读者可以自行按home回到这一页的顶端看我之前写的dfs序和倍增求lca。。。)
那么,两次dfs的代码实现如下
void dfs1(int u)
{
siz[u]=1; //对 每一个节点来说,初始的siz[]均为1
for(int i=head[u];i;i=edge[i].nxt)// 邻接链表存图
{
int v=edge[i].to; //当前要到达的下一个点
if(v==fat[u]) continue; //不要父节点走,根节点的父亲就赋成一个题目里不会出现的点
fat[v]=u;//这一步好像没有什么问题。。。。。
dep[v]=dep[u]+1;//深度+1
dfs(v);//继续dfs1
siz[u]+=siz[v];//每一个节点的大小=自己的大小(1)+所有儿子节点的大小之和。
if(siz[v]>siz[son[u]]) // 如果某一个子节点的siz[] 大于当前的重儿子的siz,则重儿子更新为这个节点
son[u]=v;
}
}
int idc=0;//用于计dfs序下标的数;
void dfs2(int u,int tp) // tp表示u通过重链能到达的深度最小的点
{
seq[++idc]=u; // 把当前节点按dfs序存进数组中
in[u]=idc; // 进入seq时候的时间戳(下标),详情见上一篇博客
if(son[u]) dfs2(son[u],tp) // 只要它有重儿子,那么它的重儿子可以到达的深度最小的点一定和它本身相等
for(int i=head[u];i=edge[i].nxt)
{
int v=edge[i].mxt;
if((v==fat[u])||(v==son[u])) continue; // 相当于排除了所有的重儿子, 也就是说在这一步没有被continue代替的点都是不在重链上的
dfs(v,v);// 所有不在重链上的点的最高可到达点是它自己
}
out[u]=idc;// 从dfs序中离开的时间戳(也就是下标),详情见上一篇博客
}而求lca的代码就比较简单了
int lca(int u,int v) //返回u和v的lca
{
while(top[u]!=top[v]) // 当它们不在一条重链上的时候,就一步一步往上跳(其实并不是一步一步啦。。每次会跳到top[u]的父亲节点上)
{
if(dep[fat[u]]<dep[fat[v]])//我们将fat[top[u]]深度更深的节点往上跳,所以要交换顺序(当然也可以不交换,就加判断条件就好啦)
{
swap(u,v);
}
u=fat[top[u]];// 往上跳
}
return dep[u]<dep[v]?u:v; //当它们跳到同一条重链的时候,就返回深度更小的那个点
}当我们把树链剖分和线段树联系在一起的时候,就终于可以做到最早提到的六种操作啦。。。。。。。。(松了一大口气.jpg)
所以让我们来看一看建线段树和链/子树的修改和查询操作。
首先还是建树(这里的建树其实和dfs序的建树是一模一样的)
/*
这里的修改操作是在某个链或者子树上面加上一个delta(如果是把区间的值改为delta的话就把所有的+=改成=就好啦,这里不涉及即增加有改值的操作,以后我会在讲主席树和各种可持久化结构的时候补充)
*/
#include<cstdio>
#include<algorithm>
using namespace std;
struct Node
{
int sum;
int vmin;
int vmax;
int tag;
bool flag;
Node *ls;
Node *rs;
void update()
{
sum=ls->sum+rs->sum;
vmax=max(ls->vmax,rs->vmax);
vmin=min(lc->vmin,rs->vmin);
}
void pushdown(int l,int r)
{
if(flag)
{
int mid=(l+r)>>1;
ls->tag+=tag;
rs->tag+=tag;
ls->sum+=tag*(mid-l+1);
rs->sum+=tag*(r-mid);
ls->flag=1;
rs->flag=1;
tag=0;
flag=0;
}
}
} pool[MAXN],*root,*tail=pool;
Node *build(int l,int r)
{
Node nd=++tail;
if(l==r)
{
nd->sum=nd->vmax=nd->vmin=seq[l];
return nd;
}
else
{
int mid=(l+r)>>1;
nd->ls=build(l,mid);
nd->rs= build(mid+1,r);
nd->update();
}
return nd;
}
void modify(Node *nd,int l,int r,const int L,const int R,const int delta)
{
if(L<=l&&R>=r)
{
nd->sum+=delta*(r-l+1);
nd-tag+=delta;
nd->flag=1;
}
nd->pushdown(l,r);
int mid=(l+r)>>1;
if(L<=mid)
{
modify(nd->ls,l,mid,L,R,delta);
}
if(R>mid)
{
modify(nd->rs,mid+1,r,L,R,delta);
}
nd->update();
}
void query(Node *nd,int l,int r,const int L,const int R)//这里查询的是区间和
{
if(L<=l&&R>=r)
{
return nd->sum;
}
nd->pushdown(l,r);
int mid=(l+r)>>1;
int ans=0;
if(L<=mid)
{
ans+=query(nd->ls,l,mid,L,R,delta);
}
if(R>mid)
{
ans+=query(nd->rs,mid+1,r,L,R,delta);
}
nd->update();
}然后便是最重要链修改和链查询的操作
void operate__modify_chain(int u,int v,long long delta)
{
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])
{
std::swap(u,v);
}
modify(root,1,idc,in[top[u]],in[u],delta);
u=fat[top[u]];
}
if(in[u]>in[v])
{
std::swap(u,v);
}
modify(root,1,idc,in[u],in[v],delta);
}
long long operate_query_chain(int u,int v)
{
long long ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])
{
std::swap(u,v);
}
ans=(ans+query(root,1,idc,in[top[u]],in[u]))%MOD;
u=fat[top[u]];
}
if(in[u]>in[v])
{
std::swap(u,v);
}
ans=(ans+query(root,1,idc,in[u],in[v]))%MOD;
return ans;
}所以说具体的操作也跟着一起变得清晰明了了(如果你能把上面的过程熟练地掌握好的话。。)
{
{
//链修改
int x,y;
long long z;
std::scanf("%d%d%lld",&x,&y,&z);
operate__modify_chain(x,y,z);
}
{
//链查询
int x,y;
std::scanf("%d%d",&x,&y);
long long sum=operate_query_chain(x,y)%MOD;
std::printf("%lld\n",sum);
}
{
//子树修改
int x,z;
std::scanf("%d%d",&x,&z);
modify(root,1,idc,in[x],out[x],z);
}
{
//子树查询
int x;
std::scanf("%d",&x);
long long sum=query(root,1,idc,in[x],out[x])%MOD;
std::printf("%lld\n",sum);
}
}