首先线段树能解决什么问题
假设有编号从1到n的n个点,每个点都存了一些信息,用[L,R]表示下标从L到R的这些点。
线段树的用处就是,对编号连续的一些点进行修改或者统计操作,修改和统计的复杂度都是O(log2(n)).
线段树的原理,就是,将[1,n]分解成若干特定的子区间(数量不超过4*n),然后,将每个区间[L,R]都分解为
少量特定的子区间,通过对这些少量子区间的修改或者统计,来实现快速对[L,R]的修改或者统计。
由此看出,用线段树统计的东西,必须符合区间加法,否则,不可能通过分成的子区间来得到[L,R]的统计结果。
线段树当然是可以维护线段信息的,因为线段信息也是可以转换成用点来表达的(每个点代表一条线段)。
符合区间加法的例子:
数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和
最大公因数(GCD)——总GCD = gcd( 左区间GCD , 右区间GCD );
最大值——总最大值=max(左区间最大值,右区间最大值)
不符合区间加法的例子:
众数——只知道左右区间的众数,没法求总区间的众数
01序列的最长连续零——只知道左右区间的最长连续零,没法知道总的最长连续零
1、结构体为什么开 4 倍空间
struct list
{
int left;
int right;
int _max;
}tree[maxn*4];
如上述代码所示,我们在写线段树的模板时,别人会告诉我们开4倍的数组就不会溢出了,然而原因是什么,现在证明一下
首先线段树是一棵二叉树,最底层有n个叶子节点(n为区间大小)深度为 k
则倒数第二层深度是 k-1
代公式 : 深度为 k ,至多 2^k -1 个结点
则 2^(k-1)-1< n <= 2^k-1
则 2^(k-1) <= n < 2^k
则 k <= log2(n) + 1
那么由此可知,此二叉树的高度为 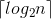
可证
然后通过等比数列求和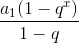
具体公式为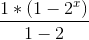
化简可得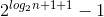
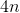
证毕
区间分解过程
线段树下标的优化方法
在线段树中,一般都不需要刻意保存其左右子结点的下标,而直接由其本身的下标导出,传统的写法是:
根结点:1
A的左子结点:2A(写成A<<1)
A的右子结点:2A+1(写成(A<<1)+1)
这种表示法可以表示出整棵线段树,因为:
(1)每个结点的子结点的下标都比它大,这样就不会出现环;
(2)每个结点的父结点都是唯一的(其本身下标整除2);
但是,这种表示法有一个弱点:结点的下标是有可能超过2N的,但不会超过4N,因此,为了表示出跨度为N的线段,我们需要开4N的空间
1、单点查询
例题:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<set>
#include<map>
#include<algorithm>
#include<queue>
#include<stack>
typedef long long LL;
using namespace std;
const int MAXX=2e5+5; // 这里我一开始写的宏定义,一直报错,后来改成了 int
#define lson l,m,i<<1 // 左儿子编号是 i×2 也就是 i<<1
#define rson m+1,r,i<<1|1 // 右儿子编号是 i×2+1 也就是 i<<1|1
struct NODE
{
int l,r,v; //区间 值
int mid() // c++ 中的函数 node[1].mid();返回值
{
return (l+r) / 2.0; // 整除
}
};
NODE node[MAXX<<2];
int maxx=0;
#define length node[i].r-node[i].l+2
void push_up(int i) // 求当前下标 i 的最大值(最大值由左右孩子比较得到的)
{
node[i].v=max(node[i<<1].v,node[i<<1|1].v);
}
void Build(int l,int r,int i)// 建树并初始化
{
node[i].l=l;
node[i].r=r;
node[i].v=0;
if(l==r) // 出口 找到叶子节点输入最后一行的信息
{
scanf("%d",&node[i].v);
return ;
}
int m=node[i].mid();
Build(lson); // 建造左子树,区间是[l,m] ,左儿子的编号是 i<<1 (乘 2)
Build(rson); // 建造右子树,区间是 [m+1,r],右儿子编号是 i<<1|1 ( 乘 2 加1)
push_up(i); // 找到之后比较最大值
}
void query(int l,int r,int i) // 查询
{
if(node[i].l==l&&node[i].r==r) // 找到了你要找的目标区间,求出来该区间的最大值
{
maxx=max(maxx,node[i].v); // 比较的原因:如果是分离式的,要比较两部分求出一个最大值
return ;
}
int m=node[i].mid();
if(r<=m) // 去左子树中查询目标区间
query(l,r,i<<1);
else{
if(l>m) // 右子树中查询目标区间
query(l,r,i<<1|1);
else // 这是目标区间的左右端点再左右子树上,分开找最大值,最后再比较一下
{
query(lson);
query(rson);
}
}
}
void update(int l,int r,int i,int number,int va) //单点更新,只更新目标区间的一个点
{
if(l==r&&l==number) //单点更新更新的是叶子节点,所以判断条件是 l 是否等于 r,并且找到该序号
{
node[i].v=va;
return ;
}
int m=node[i].mid();
if(m>=number) // 如果目标编号是小于中点的,则在左子树 [l,m] 区间中找目标编号 number
update(l,m,i<<1,number,va);
else
update(m+1,r,i<<1|1,number,va); // 在右子树找目标编号
push_up(i);// 更新完叶子节点之后,然后还要去更新它上边包含它的区间的最大值
}
int main()
{
// ios::sync_with_stdio(false);
int n,m;
char s[3]; // 我一开始输入的是单个字符有错误
int x,y;
while( scanf("%d %d",&n,&m)!=EOF){
Build(1,n,1);
while(m--)
{
scanf("%s %d %d",s,&x,&y);
maxx=0;
if(s[0]=='Q') // 最好判断 s[0]
{
query(x,y,1); // 查询的时候开始的区间是 1-n,所以一开始根节点下标是1(其实也就是编号),目标区间是 [x,y]
printf("%d\n",maxx);
}
if(s[0]=='U')
update(1,n,1,x,y); // 更新的话需要把 [1,n]都给更新,所以一开始的区间是 [1,n],第一个根节点的下标是 1,
}
}
}
2、lazy 标记(代整理)