图像缩放是将图像按照一定比例放大或者缩小,对于数字图像而言,像素的坐标是离散型非负整数,但是在进行缩放的过程中有可能产生浮点坐标值。例如,原图像坐标(9,9)在缩小一倍时会变成(4.5,4.5),这显然是一个无效的坐标。因此需要用到图像插值方法。常见的插值算法有最邻近插值法、双线性插值法,二次立方插值法,三次立方插值法等。本文主要介绍最邻近插值、双线性插值和三次立方插值,其他一些高阶的插值算法,以后再做研究。
1.最近邻插值
最近邻插值是最简单的图像缩放处理方法,其原理是提取原图像中与其邻域最近像素值来作为目标图像相对应的像素值。简单来说就是四舍五入,浮点坐标的像素值等于距离该点最近的输入图像的像素值。最邻近插值几乎没有多余的运算,速度相当快。但是这种邻近取值的方法是很粗糙的,会造成图像的马赛克、锯齿等现象。
假设原图像中的点A0(x0,y0)经过缩放后目标图像中的坐标为A1(x1,y1),x方向和y方向的缩放比例为kx与ky,则变换矩阵为:

在opencv中提供了3个浮点数转换成整数的函数,分别是cvRound、cvFloor和cvCeil。cvRound函数返回和参数最接近的整数值,四舍五入。CvFloot函数返回不大于参数的最大整数值,向下取整。cvCeil返回不小于参数的最下整数值,向上取整。
最近邻插值的实现代码如下:
void NearstInterpolation(const Mat& srcImage, Mat &dstImage, double kx, double ky)
{
CV_Assert(srcImage.data != NULL);
double inv_kx = 1.0 / kx;
double inv_ky = 1.0 / ky;
int srcRowNum = srcImage.rows;
int srcColNum = srcImage.cols;
int dstRowNum = cvRound(srcImage.rows * ky);
int dstColNum = cvRound(srcImage.cols * kx);
dstImage.create(dstRowNum, dstColNum, srcImage.type());
for(int i = 0; i < dstRowNum; i++)
{
int y = cvRound(i * inv_ky);
if(y > srcRowNum - 1)
{
y = srcRowNum - 1;
}
for(int j = 0; j < dstColNum; j++)
{
int x = cvRound(j * inv_kx);
if(x > srcColNum - 1)
{
x = srcColNum - 1;
}
dstImage.at<Vec3b>(i, j) = srcImage.at<Vec3b>(y, x);
}
}
}
2.双线性插值
双线性插值是应用最广泛的图像插值方法,它的插值效果比最邻近插值要好很多,相应的计算速度也要慢上不少。双线性插值的主要思想是计算出浮点坐标周围的四个整数坐标,将这个四个整数坐标的像素值加权平均就可以求出浮点坐标的像素值。
假设要求坐标为(2.4,3)的像素值 P,该点在(2,3)和(3,3)之间,如下图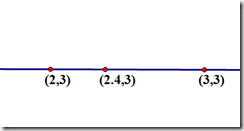
u和v分别是距离浮点坐标最近两个整数坐标像素在浮点坐标像素所占的比例(与距离成反比,离得越近,权值越大),那么P(2.4,3) = u * P(2,3)+ v * P(3,3)。上面是只在一条直线的插值,称为线性插值。双线性插值就是分别在X轴和Y轴做线性插值运算。下面利用三次的线性插值进行双线性插值运算。

(2.4,3)的像素值 F1 = (1 – m) * T1 + m* T2
(2.4,4)的像素值 F2 =(1 – m) * T3+ m * T4
(2.4,3.5)的像素值 F = (1 – n) * F1 + n* F2
这样就可以求得浮点坐标(2.4,3.5)的像素值了。 上面就是双线性插值的基本过程,假设经过过图像缩放的逆变换后目标图像的某点(x,y)在原图像的坐标为(x0,y0),其像素值为f(x0,y0),双线性插值的公式如下:
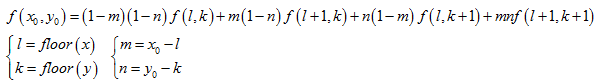
由于浮点坐标由邻域内4个坐标加权后求得,一定程度上弱化了高频分量。但如果这4个坐标的像素值差别较大,插值后,会使得图像在颜色分界较为明显的地方变得比较模糊。
双线性插值的主要代码如下:
void Biline(const Mat& srcImage, Mat& dstImage, double kx, double ky)
{
CV_Assert(srcImage.data != NULL);
double inv_kx = 1.0 / kx;
double inv_ky = 1.0 / ky;
int srcRowNum = srcImage.rows;
int srcColNum = srcImage.cols;
int dstRowNum = srcImage.rows * kx;
int dstColNum = srcImage.cols * ky;
dstImage.create(dstRowNum, dstColNum, srcImage.type());
for(int i = 0; i < dstRowNum; i++)
{
double srcy = (i + 0.5) * inv_ky - 0.5;
int k = cvFloor(srcy);
k = min(k, srcRowNum - 2);
k = max(0, k);
double n = srcy - k;
for(int j = 0; j < dstColNum; j++)
{
double srcx = j * inv_kx;
int l = cvFloor(srcx);
l = min(l, srcColNum - 2);
l = max(0, l);
double m = srcx - l;
dstImage.at<Vec3b>(i, j)[0] = (1 - m) * (1 - n) * srcImage.at<Vec3b>(k, l)[0] + m * (1 - n) * srcImage.at<Vec3b>(k, l + 1)[0]
+ n * (1 - m) * srcImage.at<Vec3b>(k + 1, l)[0] + m * n * srcImage.at<Vec3b>(k + 1, l + 1)[0];
dstImage.at<Vec3b>(i, j)[1] = (1 - m) * (1 - n) * srcImage.at<Vec3b>(k, l)[1]+ m * (1 - n) * srcImage.at<Vec3b>(k, l + 1)[1]
+ n * (1 - m) * srcImage.at<Vec3b>(k + 1, l)[1] + m * n * srcImage.at<Vec3b>(k + 1, l + 1)[1];
dstImage.at<Vec3b>(i, j)[2] = (1 - m) * (1 - n) * srcImage.at<Vec3b>(k, l)[2] + m * (1 - n) * srcImage.at<Vec3b>(k, l + 1)[2]
+ n * (1 - m) * srcImage.at<Vec3b>(k + 1, l)[2]+ m * n * srcImage.at<Vec3b>(k + 1, l + 1)[2];
}
}
}
值得一提的是上述程序中计算源坐标采用的是

原因很简单,就是坐标系的选择问题,或者说源图像和目标图像之间的对应问题。相关解释在其他博客上都可以找到,这里不再赘述。
3.双三次插值
双三次插值又叫立方卷积插值、双立方插值是一种更加复杂的插值方式,它能创造出比双线性插值更平滑的图像边缘。双三次插值利用待采样点周围16个点的灰度值作三次插值,不仅考虑到周围四个直接相邻像素点灰度值的影响,还考虑到它们灰度值变化率的影响。在这种方法中,函数 f 在点(x, y) 的值可以通过矩形网格中最近的十六个采样点的加权平均得到,在这里需要使用两个多项式插值三次函数,每个方向使用一个。更多介绍参考维基百科:
https://en.wikipedia.org/wiki/Bicubic_interpolation。
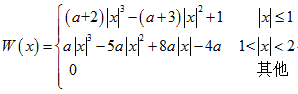
其中,a取-0.75或-0.5。
假设经过逆变换后目标图像的某点(x,y)在原图像的坐标为(x0,y0),可按下列步骤求出f(x0,y0)
代码如下:
/****************************************************************
*Name:双三次插值
*Date: 2017.02.26
*****************************************************************/
void BicubicInterpolation(const Mat& srcImage, Mat &dstImage, double kx, double ky)
{
CV_Assert(srcImage.data != NULL);
double inv_kx = 1.0 / kx;
double inv_ky = 1.0 / ky;
int srcRowNum = srcImage.rows;
int srcColNum = srcImage.cols;
int dstRowNum = srcImage.rows * kx;
int dstColNum = srcImage.cols * ky;
dstImage.create(dstRowNum, dstColNum, srcImage.type());
for(int i = 0; i < dstRowNum; i++)
{
double srcy = (i + 0.5) * inv_ky - 0.5;
int k = cvFloor(srcy);
k = min(k, srcRowNum - 3);
k = max(1, k);
double n = srcy - k;
const double A = -0.75;
double cbufY[4];
cbufY[0] = ((A * (n + 1) - 5 * A) * (n + 1) + 8 * A) * (n + 1) - 4 * A;
cbufY[1] = ((A + 2) * (n) - (A + 3)) * n * n + 1;
cbufY[2] = ((A + 2) * (1 - n) - (A + 3)) * (1 - n) * (1 - n) + 1;
cbufY[3] = ((A * (2 - n) - 5 * A) * (2 - n) + 8 * A) * (2 - n) - 4 * A;
for(int j = 0; j < dstColNum; j++)
{
double srcx = (j + 0.5) * inv_kx - 0.5;
int l = cvFloor(srcx);
l = min(l, srcColNum - 3);
l = max(1, l);
double m = srcx - l;
float cbufX[4];
cbufX[0] = ((A * (m + 1) - 5 * A) * (m + 1) + 8 * A) * (m + 1) - 4 * A;
cbufX[1] = ((A + 2) * (m) - (A + 3)) * m * m + 1;
cbufX[2] = ((A + 2) * (1 - m) - (A + 3)) * (1 - m) * (1 - m) + 1;
cbufX[3] = ((A * (2 - m) - 5 * A) * (2 - m) + 8 * A) * (2 - m) - 4 * A;
for(int cn = 0; cn < srcImage.channels(); ++cn)
{
dstImage.at<cv::Vec3b>(i, j)[cn] = saturate_cast<uchar>(srcImage.at<Vec3b>(k - 1, l - 1)[cn] * cbufX[0] * cbufY[0]
+ srcImage.at<Vec3b>(k, l - 1)[cn] * cbufX[0] * cbufY[1]
+ srcImage.at<Vec3b>(k + 1, l - 1)[cn] * cbufX[0] * cbufY[2]
+ srcImage.at<Vec3b>(k + 2, l - 1)[cn] * cbufX[0] * cbufY[3]
+ srcImage.at<Vec3b>(k - 1, l)[cn] * cbufX[1] * cbufY[0]
+ srcImage.at<Vec3b>(k, l)[cn] * cbufX[1] * cbufY[1]
+ srcImage.at<Vec3b>(k + 1, l)[cn] * cbufX[1] * cbufY[2]
+ srcImage.at<Vec3b>(k + 2, l)[cn] * cbufX[1] * cbufY[3]
+ srcImage.at<Vec3b>(k - 1, l + 1)[cn] * cbufX[2] * cbufY[0]
+ srcImage.at<Vec3b>(k, l + 1)[cn] * cbufX[2] * cbufY[1]
+ srcImage.at<Vec3b>(k + 1, l + 1)[cn] * cbufX[2] * cbufY[2]
+ srcImage.at<Vec3b>(k + 2, l + 1)[cn] * cbufX[2] * cbufY[3]
+ srcImage.at<Vec3b>(k - 1, l + 2)[cn] * cbufX[3] * cbufY[0]
+ srcImage.at<Vec3b>(k, l + 2)[cn] * cbufX[3] * cbufY[1]
+ srcImage.at<Vec3b>(k + 1, l + 2)[cn] * cbufX[3] * cbufY[2]
+ srcImage.at<Vec3b>(k + 2, l + 2)[cn] * cbufX[3] * cbufY[3]);
}
}
}
}
