机器学习&Day2

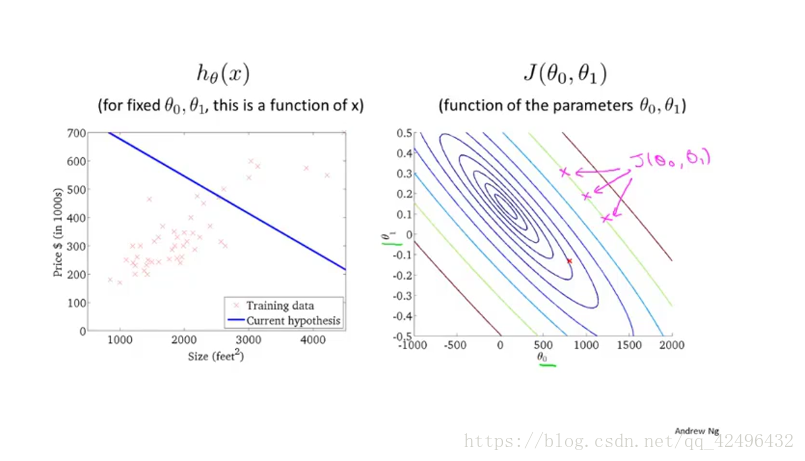
今天学习了模型描述，代价函数和梯度下降，吴恩达老师一步一步由浅入深的讲解使得我的学习没那么吃力，只是没想到学过的概率论知识和微积分知识能运用到如此神奇的地方。
首先是模型训练(model representation)：
大致过程为以下模型

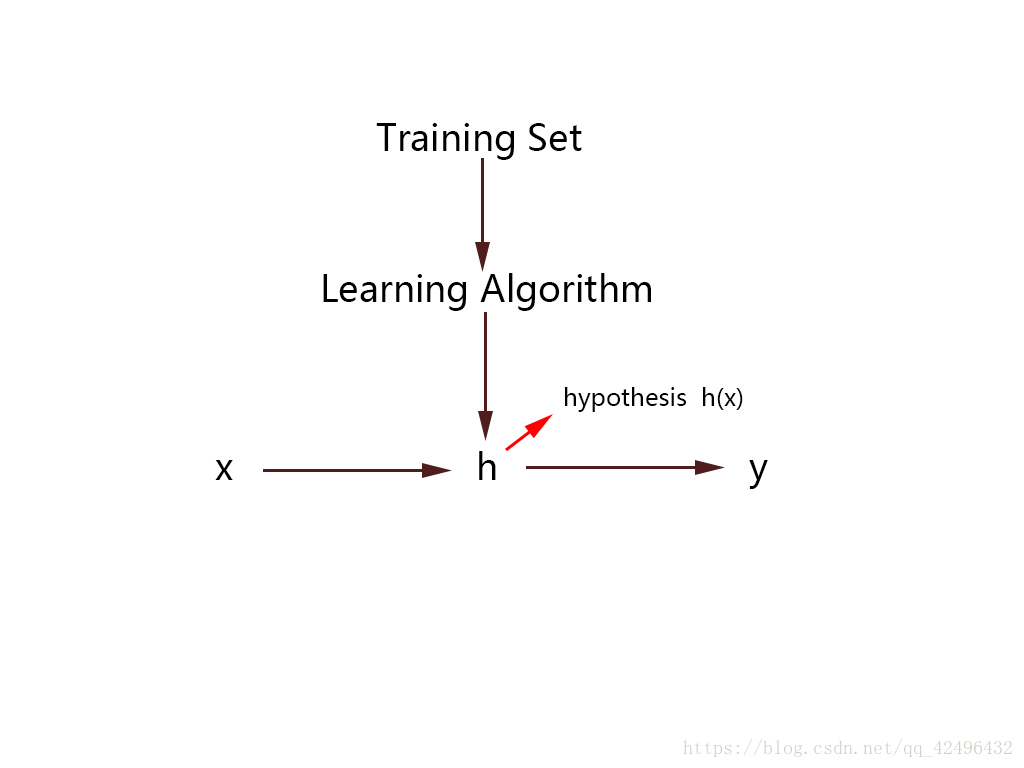
通过训练集拟合出一个函数h(x)
x为input，y为output
h是一个引导从x到y的函数

其次是代价函数(cost function)：
先假设

$$h_\theta(x)=\theta_0+\theta_1x$$
然后选择适当的 $\theta_0,\theta_1$使得 $h_\theta(x)$更接近与原函数y
最后让代价函数(cost function) $J(\theta_0,\theta_1)$
$$J(\theta_0,\theta_1)={1\over 2m}\sum_{i=0}^m(h_\theta(x^{(i)})-y^{(i)})^2$$
的值最小
觉得这个公式和概率论中的方差公式一摸一样有木有？！
这个公式也称 平方误差公式或 平方代价误差公式。
当不考虑 $\theta_0$的时候，代价函数在平面坐标中的图形就是一个向上的抛物线且与横轴最多只有一个交点， $J(\theta_1)$最小时 $\theta_1$的值便为寻找的最优目标(局部最优解)

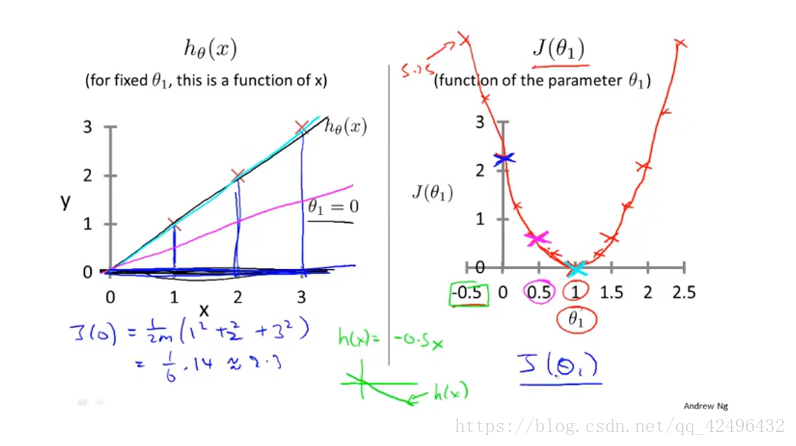
当然大多数应该考虑 $\theta_0$，此时 $J(\theta_1)$在三维平面中类似一一个碗的形状

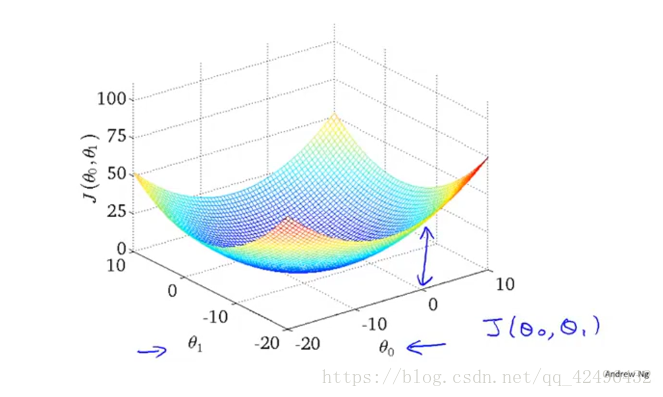
最后是梯度下降(gradient descent)：
梯度下降寻找最优解的$\theta_0和\theta_1$的过程：
首先找到一个$\theta_0和\theta_1$
然后持续改变$\theta_0和\theta_1$使得$J(\theta_0,\theta_1)$的值不断减小知道找到我们希望的最小值($J(\theta_0,\theta_1)$)
梯度下降算法为：
repeat until convergence{
$\theta_j:=\theta_j-\alpha{\delta\over \delta\theta_j}J(\theta_0,\theta_1)$
}
$\alpha$代表的是学习率(learning rate)
$\quad{\delta\over \delta\theta_j}J(\theta_0,\theta_1)$代表的是导数项(微积分中的知识)
听老师讲的是学习率代表了我们“下山”要走多大的一步
但是我当时觉得学习率和导数项的乘积才决定了“下山”要走多大的一步(在老师讲完学习率的取值大小之后才发现占主导地位的还是学习率)
其中$\theta_0和\theta_1$的更新是同步的
之后又了解到如果$\alpha$的取值太小，梯度下降寻找局部最优解的过程将会变得缓慢；但是$\alpha$的取值太大的话，梯度下降寻找局部最优解的过程中可能会跳过局部最优点，可能无法找到收敛点，甚至会发散！

以上是我今天的所学所得，共勉。