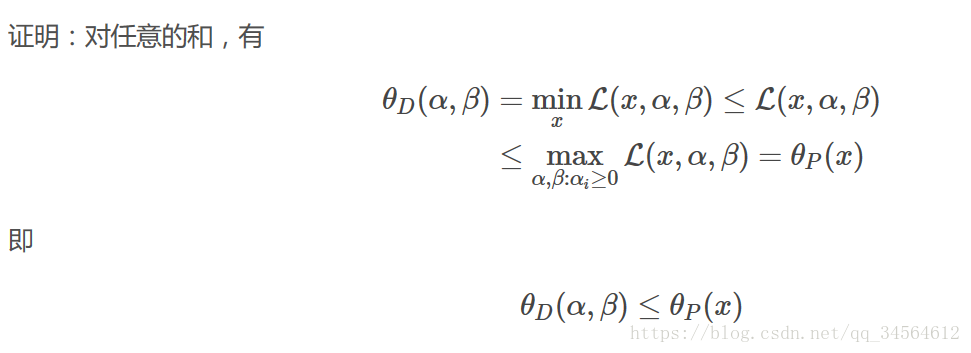普通同学的解法
- 无约束条件:求导就可以了
- 等式约束:代入消元,再求导
- 不等式约束:分情况讨论(在边界上和不在边界上),分别对应1,2的情况
然而发现,有些情况消元特别复杂,甚至不能求解
聪明同学的解法
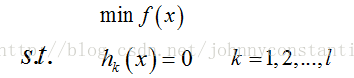
发现:在最优点的情况下,约束曲面的法向量和目标函数的梯度反向必相同或相反
拉格朗日乘子法如何理解? (在2维里可以形象的解释为z=f(x,y)在约束条件g(x,y)=c中,极值为等高线f(x,y)=k与g(x,y)=c相切的时候)
于是就有了方程: ▽f(x*)+λ▽h(x*)=0
联合这个方程和h(x)=0,在某些情况比繁琐的消元好多了,至少能求解
天才同学的解法(拉格朗日乘子法)
天才可不仅仅停留在方程求解,发现了梯度之间的关系,就可以建立新的函数(拉格朗日函数):L(x,λ)=f(x)+λh(x),分别对这个函数求偏导,即还原了初始问题。
同理,对于不等式约束问题,分情况讨论,可以建立带KKT条件的拉格朗日函数:
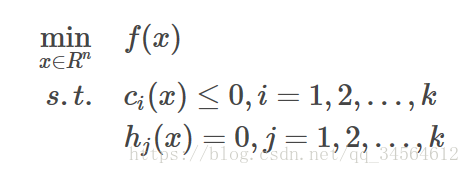
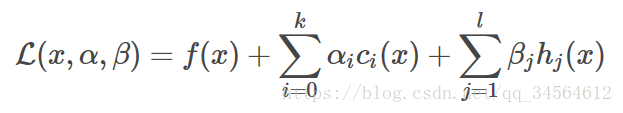
KKT条件:
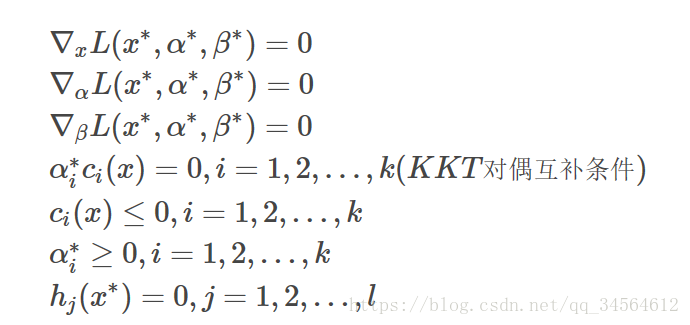
其实KKT条件就是为了和原优化问题等价而附带的一些等式和不等式
说了这么多,是不是发现并没有什么卵用,对应求导得出的还是和聪明同学的解法一样,求导解方程求解。
接下来才是关键,

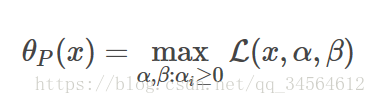
此问题称为原问题,你会很奇妙的发现:
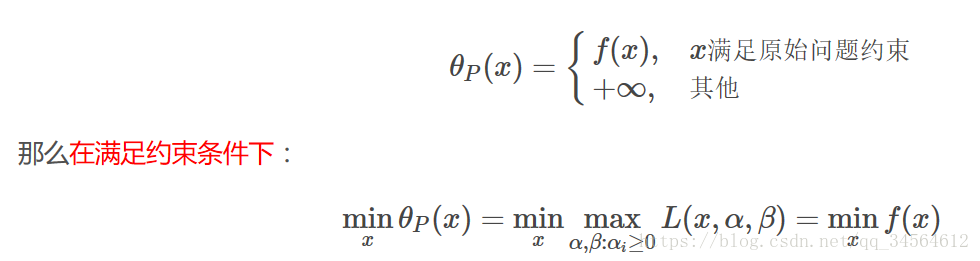
原问题只有在满足约束条件下才有极小值,等价于满足约束条件的f(x)的极小值,于是问题转化为拉格朗日极小极大问题:
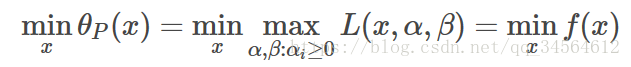
不妨设解为p*。
现在我们来直接下手求解原问题,先极大,对α,β求导,得出c(x)=0,h(x)=0,即原不等式和等式,再代入f(x),求极小,对x求导…..等等,好眼熟?不又回到了原点吗?
好在有对偶问题可以再等价= =:
对偶问题
交换极大极小的顺序(其实就是交换代入求导的顺序),转化为拉格朗日极大极小问题:

不妨设对偶问题解为d*。
现在我们来下手求解对偶问题,先极小,对x求导,得出x关于α,β的表达式,再代入f(x),再求极大,对α,β求导。
值得庆幸的是,数学家们已经证明,当f(x)和c(x)为凸函数,h(x)为仿射函数时,p*= d*。
总结
遇到等式和不等式约束优化问题怎么办:
1.引入拉格朗日函数和KKT条件,转为无约束优化问题
求导不好解怎么办:
2.转为求对偶问题,更换求导代入再求导的顺序(即先极小再极大)
注意:求解时需要满足KKT条件
普通同学的解法:消元求导
聪明同学的解法:建立梯度关系,求导,解多元方程
天才同学的解法:转为对偶问题,消元求导
在SVM的应用
SVM不就是在一大堆不等式的约束的最优化问题吗,所以当然用天才同学的解法,转为对偶问题,消元求导,可以带来以下好处:
1.方便求解
2.自然的引入核函数
在最大熵模型的应用
最大熵原理认为,学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型,简单说就是,在没有更多信息下,那些不确定的部分是“等可能的”。
也就是约束等式下,熵最大问题,可等价转为拉格朗日对偶问题。