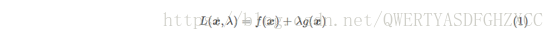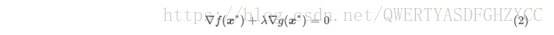1.1、定义
拉格朗日乘数法通过引入拉格朗日乘子,可将有 d 个变量与 k 个约束条件的极值问题(最优化问题)转化为具有 d+k 个变量的无约束优化问题。
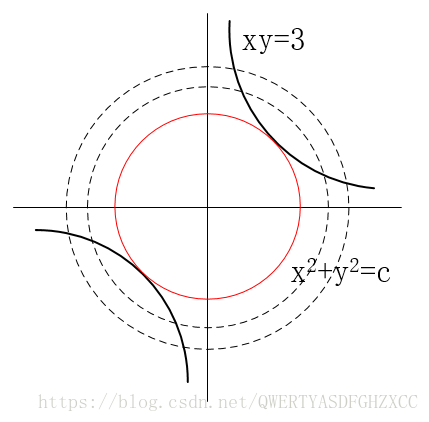
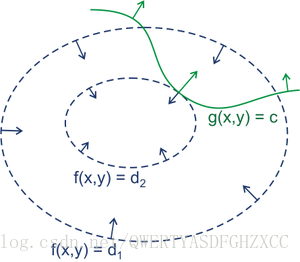
先放两张图有助于后面的理解
1.2、等式约束
假设x为d维向量,欲寻找x的最优值x∗,使目标函数f(x)最小且同时满足g(x)=0的约束。
引出拉格朗日函数
由于f(x)是凸函数,也就是x*是唯一的,可以通过下面2个式子来求x∗。
g(x*)=0
因此,原约束优化问题可转化为对拉格朗日函数(式(1))的无约束优化问题。
从几何角度看,该问题的目标是在由方程 g(x)=0 确定的 d−1 维曲面上寻找能使目标函数 f(x) 最小化的点。因此,有以下结论:
① 对于约束曲面上任意点 x,该点的梯度 ∇g(x) 正交于约束曲面;
② 在最优点 x∗,目标函数在该点的梯度∇f(x∗) 正交于约束曲面。(反证法:若梯度∇f(x∗) 与约束曲面不正交,则仍可在约束曲面上移动该点使函数值进一步下降)
即在最优点 x∗,梯度 ∇g(x) 和 ∇f(x) 的方向必相同或相反,即式(2)成立:
1.3、不等式约束
把上面的约束换成不等式约束g(x)≤0
对于g(x)<0, λ=0
对于g(x)=0,λ>0
可以推出KKT条件
1.4、对偶性