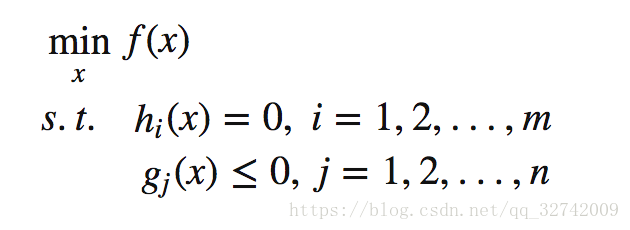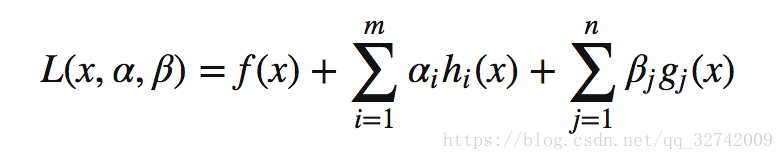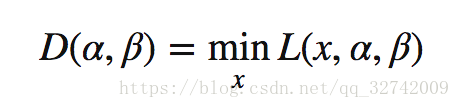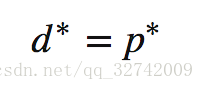继介绍完拉格朗日乘子法与KKT条件之后,再来讲讲拉格朗日对偶变换。
为接下来彻底搞清楚SVM做好铺垫。
在优化理论中,目标函数会有多种形式:如果目标函数和约束条件都为变量
的线性函数, 称该问题为线性规划; 如果目标函数为二次函数, 约束条件为线性函数, 称该最优化问题为二次规划; 如果目标函数或者约束条件均为非线性函数, 称该最优化问题为非线性规划。每个线性规划问题都有一个与之对应的对偶问题,对偶问题有非常良好的性质,以下列举几个:
- 对偶问题的对偶是原问题;
- 无论原始问题是否是凸的,对偶问题都是凸优化问题;
- 对偶问题可以给出原始问题一个下界;
- 当满足一定条件时,原始问题与对偶问题的解是完全等价的;
比如下边这个例子,虽然原始问题非凸,但是对偶问题是凸的:
在这边多插一句嘴,关于非线性规划的问题,在matlab中大概又四种算法:内点法,SQP序列二次规划,信赖域反射算法(针对大规模问题),active set(有效集算法)。以后有时间会再学习和撰写相关算法的。
在开始讲拉格朗日对偶问题之前,翻出了久违的运筹学书本,先直观的介绍一下对偶问题是什么,以及它怎么由原始问题获得,以及一些简单的性质。
原问题与对偶问题的关系:简单了说,如果原问题是一个在一定的约束下,最大化一个企业的生产利润。那么它的对偶问题就是希望用最小代价把这个企业的所有资源收购过来。
原问题与对偶问题简单例子:
原问题:
max
对偶问题:
min
原问题与对偶问题变换规则:
- 原问题是求极大,对偶问题就是求极小,反之同理。
- 一个问题中的约束条件个数等于另一个问题中的变量数。
- 一个问题中目标函数的系数是另一个问题中约束条件的右端项。
- 约束条件在一个问题中为“
”,则在另一个问题中为“
”。
原问题与对偶问题的性质:
性质的具体内容在这里不做过多的介绍,毕竟理解起来也不是那么的快的。就说一下名字,有兴趣的可以自行baidu,在拉格朗日对偶变换中用到的性质会在后文中详细介绍。
- 弱对偶性
- 最优性
- 无界性
- 强对偶性
- 互补松弛性
开始进入正题!
原始问题
首先给出不等式约束优化问题:
定义 Lagrangian 如下:
根据以上 Lagrangian 便可以得到一个重要结论:
这段话需要多读几遍,确保理解。后面半句中,如果等式条件不被满足,且等式条件为负,那就让乘子变成负无穷大,同样会得到L无穷大,依旧会导致问题无解。故必须满足约束条件。
对偶问题
上式与原优化目标等价,将之称作原始问题 , 将原始问题的解记做,如此便把带约束问题转化为了无约束的原始问题,其实只是一个形式上的重写,方便找到其对应的对偶问题,首先为对偶问题定义一个对偶函数(dual function) :
直观地,可以理解为最小的里最大的那个要比最大的中最小的那个要大。具体的证明过程如下:
这个性质便叫做弱对偶性(weak duality),对于所有优化问题都成立,即使原始问题非凸。
弱对偶性的正常定义是原问题如果为极大,则有原问题的任何可行解小于等于对偶问题。反之则大于等于。
这里不必太过纠结,都是定义上的东西。实在不行可以举个例子来理解。
看完这些,应该可以接受上面的定义了吧。
这里还有两个概念:
之前提过无论原始问题是什么形式,对偶问题总是一个凸优化的问题,这样对于那些难以求解的原始问题 (甚至是 NP 问题),均可以通过转化为偶问题,通过优化这个对偶问题来得到原始问题的一个下界, 与弱对偶性相对应的有一个强对偶性(strong duality) ,强对偶即满足:
强对偶是一个非常好的性质,因为在强对偶成立的情况下,可以通过求解对偶问题来得到原始问题的解,在 SVM 中就是这样做的。当然并不是所有的对偶问题都满足强对偶性 ,在 SVM 中是直接假定了强对偶性的成立,其实只要满足一些条件,强对偶性是成立的,比如说 Slater 条件与KKT条件。
Slater 条件
也就是说如果原始问题是凸优化问题并且满足 Slater 条件的话,那么强对偶性成立。需要注意的是,这里只是指出了强对偶成立的一种情况,并不是唯一的情况。例如,对于某些非凸优化的问题,强对偶也成立。SVM 中的原始问题 是一个凸优化问题(二次规划也属于凸优化问题),Slater 条件在 SVM 中指的是存在一个超平面可将数据分隔开,即数据是线性可分的。当数据不可分时,强对偶是不成立的,这个时候寻找分隔平面这个问题本身也就是没有意义了,所以对于不可分的情况预先加个 kernel 就可以了。
KKT条件
当原始问题为凸优化问题的时候,其对偶问题的强对偶性与KKT条件是互为充要的。
当原始问题不为凸优化问题是,利用其对偶问题也可以得到原问题最优解的下界。
参考文章: