概率论与数理统计——二元均匀和正态分布

1、二元均匀分布

     若二元随机变量 的概率密度在平面上的一个有界区域 D内是常数，而在其余地方取值为零，称(X,Y) 在上 D 服从均匀分布。    设    其中A为区域D的面积。

     

2、二元正态分布

3、随机变量的独立性

（1）独立性定义：

       设F(x,y)是二元随机变量(X,Y)的分布函数， 是Y的边际分布函数，若对所有x,y有：

                   即   

       称随机变量x,y相互独立。

（2）独立性等价判断：

• 离散型：用分布律判断。对一切i，j都成立  即  
• 连续型：用密度函数判断。对在平面的点(x,y)几乎处处成立  .

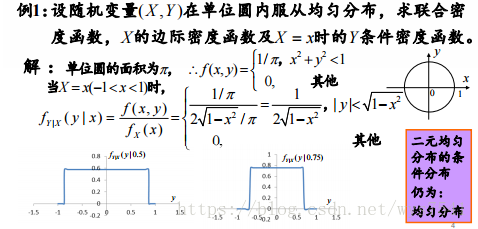
（3）实例及结论

     

（4）一般n元随机变量的一些概念和结果