【算法图解】读书笔记

一、算法简介

二分查找的速度比简单查找快得多。
O（logn）比O（n）快。需要搜索的元素越多,前者比后者就快得越多。
算法运行时间并不以秒为单位。
算法运行时间是从其增速地角度度量的。
算法运行时间用大O表示法表示。

二、选择排序

2.1 内存的工作原理

如同寄存柜，每个柜子有很多抽屉，你有几样东西寄存就需要几个抽屉，这大致就是计算机内存的工作原理计算机就像每个抽屉的集合体，每个抽屉都有地址。

需要将数据存储到内存时，你请求计算机提供存储空间，计算机给你一个存储地址，需要存储多项数据时，有两种基本方式——数组和链表。但它们并非都适用于所有的情形，因此知道它们的差别很重要。

2.2 数组和链表

2.2.1 链表

链表中的元素可存储在内存的任何地方。

链表的每个元素都存储了下一个元素的地址，从而使一系列随机的内存地址串在一起。

在链表中添加元素很容易，只需将其存入内存，并将其地址存储到前一个元素中。

使用链表时，根本就不需要移动元素，只要有足够的内存空间，就能为链表分配内存。

链表的优势在插入元素方面

2.2.2 数组

在需要读取链表的最后一个元素时，你不能直接读取，因为你不知道他所处的地址，必须先访问元素#1，从中获取元素#2的地址，再访问#2并从中获取#3的地址，以此类推，直到访问最后一个元素。需要同时读取所有元素时，链表的效率很高：读取第一个元素，根据其中的地址再读取第二个元素，以此类推。如果需要跳跃，链表的效率真的很低。

数组与此不同：你知道其中每个元素的地址。例如一个数组包含5个元素，起始地址是00，那么元素#5的地址就是04。需要随机地读取元素时，数组的效率很高，因为可迅速找到数组的任何元素。而在链表中，元素并非靠在一起，所以无法迅速算出第5个元素的内存地址，必须从第一个开始访问。

2.2.3 术语

几乎所有的编程语言都从0开始对数组元素进行编号。

元素的位置称为索引。

2.2.4 在中间插入

需要在中间插入元素时，使用链表时，插入元素很简单，只需修改它前面的那个元素指向的地址。而使用数组时，则必须将后面的元素都向后移。如果没有足够的空间，可能还得将整个数组复制到其他地方！因此，当需要在中间插入元素时，链表是更好的选择。

2.2.5 删除

如果需要删除元素，链表也是更好的选择，因为只需修改前一个元素指向的地址即可。而使用数组时，删除元素后，必须将后面的元素都向前移。

不同于插入，删除元素总能成功。如果内存中没有足够的空间，插入操作可能失败，但在任何情况下都能将元素删除。

常见数组和链表操作的运行时间：

运行时间对比

有两种访问方式：随机访问和顺序访问。顺序访问意味着从第一个元素开始逐个地读取元素。链表只能顺序访问：要读取链表的第10个元素，得先读取前9个元素，并沿链接找到第10个元素，随机访问意味着可直接跳到第10个元素。数组的读取速度更快是因为它们支持随机访问。很多情况都要求能够支持随机访问，因此数组用得比较多。

2.3选择排序

假如你的计算机存储了很多乐曲，对于每个乐队，你都记录了其作品被播放的次数。

你要将这个列表按播放次数从多到少的顺序排列，从而将你喜欢的乐队排序。该如何做？

一种办法是遍历这个列表，找出作品播放次数最多的乐队，并将该乐队添加到一个新列表中。

再次这样做，找出播放次数第二多的乐队。

继续这样做，你将得到一个有序列表

对列表进行简单查找时，意味着每个乐队都要查看一次。要找出播放次数最多的乐队，必须检查列表中的每个元素。这需要的时间为O(n)。对于这种时间为 O(n)的操作，你需要执行n次。需要的总时间为O(n * n),即O(n^2)。

选择排序是一种灵巧的算法，但其速度不是很快。

示例代码

下述代码提供了类似的功能：将数组元素按从小到大的顺序排列。

# 先编写一个用于找出数组中最小元素的函数
def findSmallest(arr):
    smallest = arr[0] # 存储最小的值
    smallest_index = 0 # 存储最小元素的索引
    for i in range(1,len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index

# 使用这个函数来编写排序算法
def selectionSort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = findSmallest(arr) # 找出数组中最小的元素并将其加入到新数组中
        newArr.append(arr.pop(smallest))
    return newArr


print selectionSort([5,3,6,2,10])

2.4 小结

计算机内存犹如一大堆抽屉。
需要存储多个元素时，可以使用数组或链表。
数组的元素都在一起。
链表的元素是分开的，其中每个元素都存储了下一个元素的地址。
数组的读取速度很快。
链表的插入和删除速度很快。
在同一个数组中，所有元素的类型都必须相同。

三、递归

3.1 递归

钥匙放在一个盒子里，这个盒子里有盒子，而盒子里的盒子又有盒子，钥匙就在某个盒子中，为找到钥匙，

下面是一种方法：

（1）创建一个要查找的盒子堆。

（2）从盒子堆里取出一个盒子在里面找。

（3）如果找到的是盒子，就将其放入盒子堆中，以便以后再查找。

（4）如果找到钥匙，则大功告成！

（5）回到第2步

使用的是while循环，只要盒子堆不空，就从中取盒子，并在其中仔细查找。

下面是另一种方法：

（1）检查盒子中的每样东西。

（2）如果是盒子，回到第一步。

（3）如果是钥匙，就大功告成！

使用递归——函数调用自己

这两种方法作用相同，第二种更清晰，递归只是让解决方案更清晰，并没有性能上的优势。

3.2 基线条件和递归条件

由于递归函数调用自己，因此编写这样的函数时很容易出错，进而导致无限循环。

编写递归函数时，必须告诉它何时停止递归。正因如此，每个递归函数都有两部分：基线条件和递归条件。递归条件指的是函数调用自己，而基线条件则指函数不再调用自己，从而避免形成无限循环。

3.3 栈

假设你去野外烧烤，并为此创建了一个待办事项清单——一叠便条。

插入的待办事项放在清单的最前面；读取待办事项时，你只读取最上面的那个，并将其删除。因此这个待办事项清单只有两种操作：压入（插入）和弹出（删除并读取）。

这种数据结构称为栈。

3.3.1 调用栈

计算机在内部使用被称为调用栈的栈。计算机是如何使用调用栈的？下面是一个简单的函数。

def greet(name):
    print "hello, " + name + "!"
    greet2(name)
    print "getting ready to say bye..."
    bye()
# 这个函数问候用户,再调用另外两个函数.另外两个函数的代码如下:

def greet2(name):
    print "how are you, " + name + "?"
    def bye():
    print "ok bye!"

下面详细介绍调用函数时发生的情况。

假设你调用greet（“maggie”），计算机将首先为该函数调用分配一块内存。

我们来使用这些内存。变量name被设置为maggie，这需要存储到内存中。

每当你调用函数时，计算机都像这样将函数调用涉及的所有变量的值存储到内存中。接下来，你打印hello，maggie！，再调用greet2（“maggie”）。同样，计算机也为这个函数调用分配一块内存。

计算机使用一个栈来表示这些内存块，其中第二个内存块位于第一个内存块上面。你打印how are you，maggie？，然后从函数调用返回。此时，栈顶的内存块被弹出。

现在，栈顶的内存块是greet的，这意味着你返回了函数greet。当你调用函数greet2时，函数greet只执行了一部分：调用另一个函数时，当前函数暂停并处于未完成状态。该函数所有变量的值都还在内存中。执行完函数greet2后，回到函数greet，并从离开的地方开始接着往下执行：首先打印getting ready to say bye...，再调用函数bye。

在栈顶添加了bye的内存块。然后，打印ok bye！，并从这个函数返回。

现在又回到了函数greet。由于没有别的事情要做，就从函数greet返回，这个栈用于存储多个函数的变量，被称为调用栈。

3.3.2 递归调用栈

递归函数也适用调用栈！下面是计算阶乘的递归函数。

def fact(x):
    if x == 1:
        return 1
    else:
        return x * fact(x-1)

每个fact调用斗鱼自己的x变量，在一个函数调用中不能访问另一个的x变量。

栈在递归中扮演着重要角色。回到寻找钥匙的两种方法。使用第一种方法时，创建了一个待查找的盒子堆，因此你始终知道还有多少盒子待查找。

但使用递归方法时，没有盒子堆。“盒子堆”存储在了栈中！这个栈包含未完成的函数调用，每个函数调用都包含还未检查完的盒子。使用栈很方便，因为无需自己跟踪盒子堆——栈代替你这样做了。

使用栈虽然方便，但是也要付出代价：存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存，如果栈很高，就意味着计算机存储了大量函数调用的信息。你只能：

重新编写代码，转而使用循环。
使用尾递归（一个高级递归主题，但并非所有的语言都支持）

3.4 小结

递归指的是调用自己的函数。
每个递归函数都有两个条件：基线条件和递归条件。
栈有两种操作：压入和弹出。
所有函数调用都进入调用栈。
调用栈可能很长，这将占用大量的内存。

四、快速排序

4.1 分而治之

分而治之（divide and conquer,D&C) —— 一种著名的递归式问题解决方法。

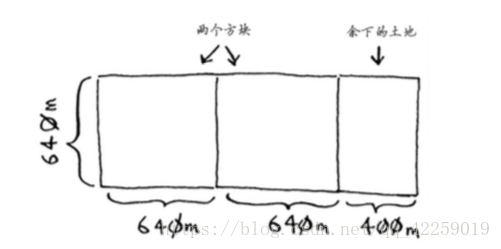
假设你是农场主，有一小块土地。你要将这块地均匀地分成方块，且分出的方块要尽可能大。如何来实现呢？使用D&C策略！D&C算法是递归的。使用D&C解决问题的过程包括两个步骤。

（2）不断将问题分解（或者说缩小规模），直到符合基线条件。

首先，找出基线条件。最容易处理的情况是，一条边的长度是另一条边的整数倍。

如果一边长25m，另一边长50m，那么可使用的最大方块为25m * 25m。换言之，可以将地分成两个这样的方块。

然后需要找出递归条件，这正是D&C的用武之地。根据D&C的定义，每次递归调用都必须缩小问题的规模。如何缩小前述问题的规模呢？首先找出这块地可容纳的最大方块。

划分完余下一小块土地，何不对余下的一小块地使用相同的算法呢？

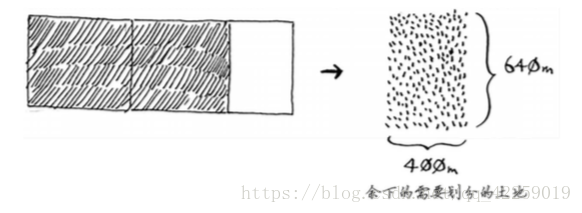
最初要划分的土地尺寸为1680m * 640m，而现在需要划分的土地更小，为640m*400m。适用于这小块地的最大方块，也是适用于整块地的最大方块（不好理解，参阅欧几里得算法）。换言之，你将均匀划分1680m * 640m土地的问题，简化成了均匀划分640m*400m土地的问题！

下面再次使用同样的算法。对于640 m × 400 m的土地，可从中划出的最 10 大方块为400 m × 400 m。

这将余下一块更小的土地，其尺寸为400 m × 240 m。

你可从这块土地中划出最大的方块，余下一块更小的土地，其尺寸为240 m × 160 m。

接下来，从这块土地中划出最大的方块，余下一块更小的土地。

余下的这块土地满足基线条件，因为160是80的整数倍。将这块土地分成两个方块后，将不会余下任何土地!

因此，对于最初的那片土地，适用的最大方块为80 m× 80 m。

重申一下D&C的工作原理：

（1）找出简单的基线条件；

（2）确定如何缩小问题的规模，使其符合基线条件。

D&C并非可用于解决问题的算法，而是一种解决问题的思路。

另一个例子：给定一个数字数组，你需要将这些数字相加，并返回结果，循环很容易完成这种任务。

def sum(arr):
    total = 0
    for x in arr:
        total += x
    return total

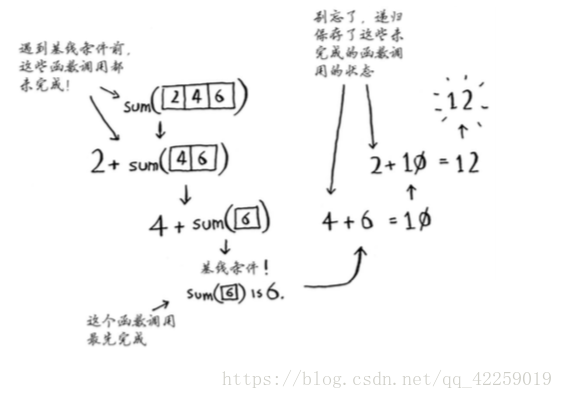
print sum([1,2,3,4])

如何使用递归函数来完成这种任务呢？

提示：编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素。

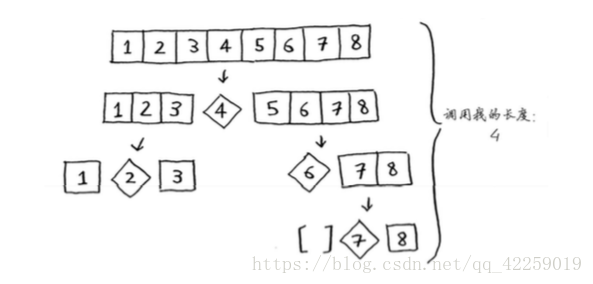
4.2 快速排序

使用快速排序对数组进行排序。

基线条件为数组为空或只包含一个元素。在这种情况下，只需原样返回数组——根本不用排序。

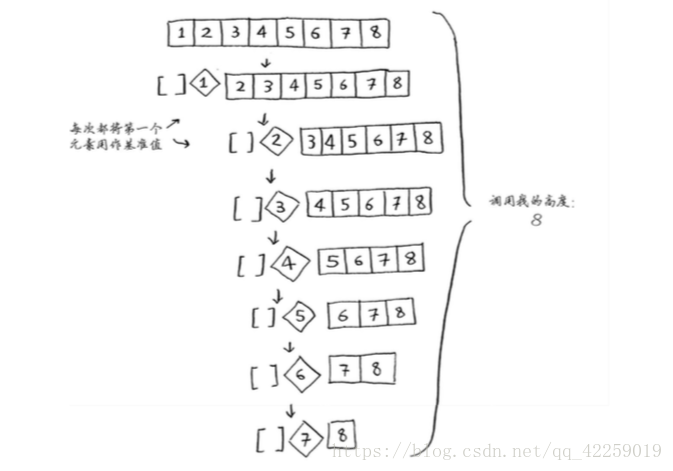
要使用D&C，需要将数组分解，直到满足基线条件。下面介绍快速排序的工作原理。首先从数组中选择一个元素，这个元素被称为基准值。

暂时将数组的第一个元素用作基准值。

接下来，找出比基准值小的元素以及比基准值大的元素。

这被称为分区。现在有：

一个由所有小于基准值的数字组成的子数组；
基准值；
一个由所有大于基准值的数字组成的子数组；

只是进行了分区，得到的子数组是无序的。

如果是有序的对整个数组进行排序将非常容易，可以合并得到一个有序的数组。

如何对子数组进行排序呢？

（1）选择基准值。

（2）将数组分成两个子数组：小于基准值的元素和大于基准值的元素。

（3）对这两个子数组进行快速排序

不管如何选择基准值，都可以对划分得到的两个数组递归地进行快速排序。

快速排序的代码：

def quicksort(array):
    if len(array) < 2:
        return array # 基线条件:为空或只包含一个元素地数组是"有序"的
    else:
        pivot = array[0] # 递归条件
        less = [i for i in array[1:] if i <= pivot] # 由所有小于基准值的元素组成的子数组
        greater = [i for in in array[1:] if i > pivot] # 由所有大于基准值的元素组成的子数组
        return quicksort(less) + [pivot] + quicksort(greater)

print quicksort([10,5,2,3])

4.3 再谈大O表示法

最常见的大O运行时间：

4.3.1 比较合并排序和快速排序

假设有下面这样打印列表中每个元素的简单函数。


def print_items(list): 
    for item in list:
        print item

from time import sleep 
def print_items2(list):
    for item in list: 
        sleep(1)
        print item

这两个函数都迭代整个列表一次，因此它们的运行时间都为O(n)。

虽然使用大O表示法表示时，这两个函数的速度相同，但实际上print_items的速度更快。在大O表示法O(n) 8 中，n实际上指的是这样的。

c是算法所需的固定时间量，被称为常量。例如，print_ items所需的时间可能是10毫秒 * n，而print_items2所需的时间为1秒 * n。

通常不考虑这个常量，因为如果两种算法的大O运行时间不同，这种常量将无关紧要。就拿二分查找和简单查找来举例说明。假设这两种算法的运行时间包含如下常量。

简单查找：10毫秒 * n

二分查找：1秒 * logn

看似简单查找要快得多，现在假设你要在包含40亿个元素的列表中查找，所需时间将如下。

简单查找：10毫秒 * 40亿 = 463天

二分查找：1秒 * 32 = 32秒

可见，二分查找的速度还是快很多，常量根本没什么影响。

但有时候，常量的影响可能很大，对快速查找和合并查找来说就是如此。快速查找的常量比合并查找小，因此如果它们的运行时间都为O(n log n)，快速查找的速度将更快。实际上，快速查找的速度确实更快，因为相对于遇上最糟情况，它遇上平均情况的可能性要大得多。

4.3.2 平均情况和最糟情况

快速排序的性能高度依赖于你选择的基准值，假设你总是将第一个元素用作基准值，且要处理的数组是有序的。由于快速排序算法不检查输入数组是否有序，因此它依然尝试对其进行排序。

注意，数组并没有被分成两半，相反，其中一个子数组始终为空，这导致调用栈非常长。现在假设你总是将中间的元素用作基准值，在这种情况下，调用栈如下。

调用栈短得多!因为你每次都将数组分成两半，所以不需要那么多递归调用。你很快就到达了基线条件，因此调用栈短得多。

第一个示例展示的是最糟情况，而第二个示例展示的是最佳情况。在最糟情况下，栈长为 O(n)，而在最佳情况下，栈长为O(log n)。

在这个示例中，层数为O(log n)(用技术术语说，调用栈的高度为O(log n))，而每层需要的时间为O(n)。因此整个算法需要的时间为O(n) * O(log n) = O(n log n)。这就是最佳情况。

在最糟情况下，有O(n)层，因此该算法的运行时间为O(n) * O(n) = O(n2)。

知道吗?这里要告诉你的是，最佳情况也是平均情况。只要你每次都随机地选择一个数组元素作为基准值，快速排序的平均运行时间就将为O(n log n)。快速排序是最快的排序算法之一，也是D&C典范。

4.4 小结

D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或只包含一个元素的数组。
实现快速排序时，请随机地选择用作基准值的元素，快速排序的平均时间为O（n logn）。
大O表示法中的常量有时候事关重大，这就是快速排序比合并排序块的原因所在。
比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O（logn）的速度比O（n）快得多。

五、散列表

5.1 散列函数

散列函数是这样的函数，即无论你给它什么数据，它都还你一个数字。

用专业术语来表达的话，我们会说，散列函数“将输入映射到数字”。散列函数必须满足一些要求。

它必须是一致的。例如，假设你输入apple时得到的是4，那么每次输入apple时，得到的都必须为4。如果不是这样，散列表将毫无用处。
它应将不同的输入映射到不同的数字。例如，如果一个散列函数不管输入是什么都返回1，它就不是好的散列函数。最理想的情况是，将不同的输入映射到不同的数字。

创建一个空数组，你将在这个数组中存储商品的价格。散列函数能准确地指出价格的存储位置，根本不用查找！之所以能够这样，具体原因如下。

散列函数总是将相同的输入映射到相同的索引。
散列函数总是将不同的输入映射到不同的索引。
散列函数知道数组有多大，只返回有效的索引。

你结合使用散列函数和数组创建了一种被称为散列表(hash table)的数据结构。散列表是你学习的第一种包含额外逻辑的数据结构。数组和链表都被直接映射到内存，但散列表更复杂，它使用散列函数来确定元素的存储位置。

在学习复杂数据结构中，散列表可能是最有用的，也被称为散列映射、映射、字典和关联数组。散列表的速度很快!

散列表由键和值组成。在前面的散列表book中，键为商品名，值为商品价格。散列表将键映射到值。

5.2 应用案例

5.2.1 将散列表用于查找

创建一个电话簿，实现添加联系人及其电话号码，通过输入联系人来获悉其电话号码。

这非常适合使用散列表来实现!

散列表被用于大海捞针式的查找。例如，你在访问像http://adit.io这样的网站时，计算机必须将adit.io转换为IP地址。

无论你访问哪个网站，其网址都必须转换为IP地址。

这不是将网址映射到IP地址吗?好像非常适合使用散列表啰!这个过程被称为DNS解析 (DNS resolution)，散列表是提供这种功能的方式之一。

5.2.2 防止重复

假设你负责管理一个投票站。显然，每人只能投一票，但如何避免重复投票呢?有人来投票时，你询问他的全名，并将其与已投票者名单进行比对。如果名字在名单中，就说明这个人投过票了，因此将他拒之门外!否则，就将他的姓名加入到名单中，并让他投票。现在假设有很多人来投过了票，因此名单非常长。

为此，首先创建一个散列表，用于记录已投票的人。

有人来投票时，检查他是否在散列表中。在散列表中，函数get将返回它;否则返回None。

5.2.3 将散列表用作缓存

最后一个应用案例:缓存。如果你在网站工作，可能听说过进行缓存是一种不错的做法。下面简要地介绍其中的原理。假设你访问网站facebook.com。

(1) 你向Facebook的服务器发出请求。

(2) 服务器做些处理，生成一个网页并将其发送给你。

(3) 你获得一个网页。

你每次访问facebook.com，其服务器都需考虑你感兴趣的是什么内容。但如果你没有登录，看到的将是登录页面。每个人看到的登录页面都相同。Facebook被反复要求做同样的事情:“当我注销时，请向我显示主页。”有鉴于此，它不让服务器去生成主页，而是将主页存储起来，并在需要时将其直接发送给用户。

这就是缓存，具有如下两个优点。

用户能够更快地看到网页
Facebook需要做的工作更少。

缓存是一种常用的加速方式，所有大型网站都使用缓存，而缓存的数据则存储在散列表中!

Facebook不仅缓存主页，还缓存About页面、Contact页面、Terms and Conditions页面等众多其他的页面。因此，它需要将页面URL映射到页面数据。

facebook.com/about ——> About页面的数据

facebook.com ——> 主页的数据

当你访问Facebook的页面时，它首先检查散列表中是否存储了该页面。

cache = {}

def get_page(url):
    if cache.get(url):
        return cache[url] # 返回缓存的数据
    else:
        data = get_data_form_server(url)
        cache[url] = data # 先将数据保存到缓存中
        return data

仅当URL不在缓存中时，你才让服务器做些处理，并将处理生成的数据存储到缓存中，再返回它。这样，当下次有人请求该URL时，你就可以直接发送缓存中的数据，而不用再让服务器进行处理了。

5.2.4 小结

散列表适合用于：

模拟映射关系；
防止重复；
缓存/记住数据，以免服务器再通过处理来完成它们。

5.3 冲突

处理冲突的方式很多，最简单的办法如下:如果两个键映射到了同一个位置，就在这个位置存储一个链表。

散列函数很重要。前面的散列函数将所有的键都映射到一个位置，而最理想的情况是，散列函数将键均匀地映射到散列表的不同位置。

如果散列表存储的链表很长，散列表的速度将急剧下降。然而，如果使用的散列函数很好，这些链表就不会很长!

5.4 性能

简单查找的运行时间为线性时间，二分查找为对数时间，散列表中查找为常量时间O（1）。

在平均情况下，散列表的查找(获取给定索引处的值)速度与数组一样快，而插入和删除速度与链表一样快，因此它兼具两者的优点!但在最糟情况下，散列表的各种操作的速度都很慢。因此，在使用散列表时，避开最糟情况至关重要。为此，需要避免冲突。而要避免冲突，需要有:

较低的填装因子；
良好的散列函数。

5.5 小结

可以结合散列函数和数组来创建散列表。
冲突很糟糕，应使用可以最大限度减少冲突的散列函数。
散列表的查找、插入和删除速度都非常快。
散列表适用于模拟映射关系。
一旦填装因子超过0.7，就该调整散列表的长度。
散列表可用于缓存数据（例如在Web服务器上）。
散列表非常适用于防止重复。

六、广度优先搜索

6.1 图简介

你经常要找出最短路径，这可能是前往朋友家的最短路径，也可能是国际象棋中把对方将死的最少步数。解决最短路径问题的算法被称为广度优先搜索。

6.2 图是什么

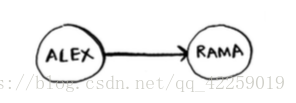
图模拟一组连接。例如，假设你与朋友玩牌，并要模拟谁欠谁钱，可像下面这样指出Alex欠Rama钱。

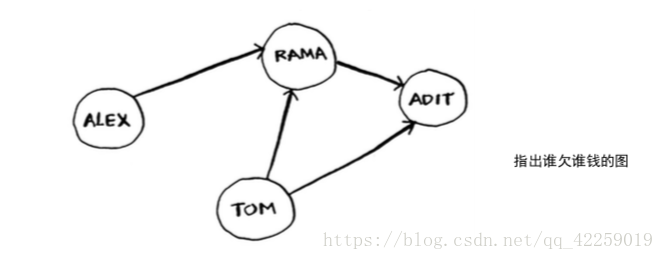
完整的欠钱图可能类似于下面这样。

Alex欠Rama钱，Tom欠Adit钱，等等。图由节点(node)和边(edge)组成。

就这么简单!图由节点和边组成。一个节点可能与众多节点直接相连，这些节点被称为邻居。在前面的欠钱图中，Rama是Alex的邻居。Adit不是Alex的邻居，因为他们不直接相连。但Adit既是Rama的邻居，又是Tom的邻居。

图用于模拟不同的东西是如何相连的。

6.3 广度优先搜索

广度优先搜索是一种用于图的查找算法，可帮助回答两类问题。

第一类问题:从节点A出发，有前往节点B的路径吗?
第二类问题:从节点A出发，前往节点B的哪条路径最短?

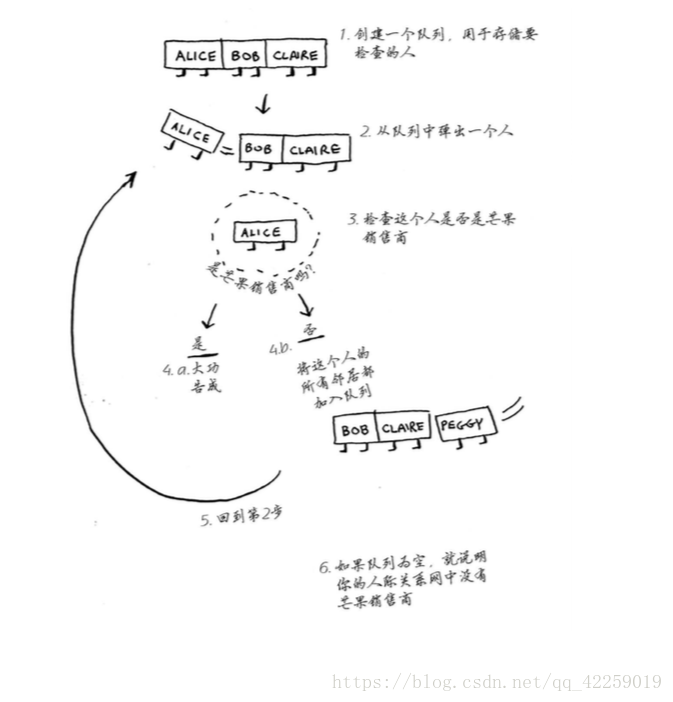
假设你经营着一个芒果农场，需要寻找芒果销售商，以便将芒果卖给他。在Facebook，你与芒果销售商有联系吗?为此，你可在朋友中查找。

这种查找很简单。首先，创建一个朋友名单。

然后，依次检查名单中的每个人，看看他是否是芒果销售商。

假设你没有朋友是芒果销售商，那么你就必须在朋友的朋友中查找。

检查名单中的每个人时，你都将其朋友加入名单。

因此，如果Alice不是芒果销售商，就将其朋友也加入到名单中。这意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网，直到找到芒果销售商。这就是广度优先搜索算法。

6.3.1 查找最短路径

刚才你看到了如何回答第一类问题，下面来尝试回答第二类问题——谁是关系最近的芒果销售商。例如，朋友是一度关系，朋友的朋友是二度关系。

在你看来，一度关系胜过二度关系，二度关系胜过三度关系，以此类推。因此，你应先在一度关系中搜索，确定其中没有芒果销售商后，才在二度关系中搜索。广度优先搜索就是这样做的! 在广度优先搜索的执行过程中，搜索范围从起点开始逐渐向外延伸，即先检查一度关系，再检查二度关系。

注意，只有按添加顺序查找时，才能实现这样的目的。有一个可实现这种目的的数据结构，那就是队列(queue)。

6.3.2 队列

队列的工作原理与现实生活中的队列完全相同。队列类似于栈，你不能随机地访问队列中的元素。队列只支持两种操作:入队和出队。

如果你将两个元素加入队列，先加入的元素将在后加入的元素之前出队。因此，你可使用队列来表示查找名单!这样，先加入的人将先出队并先被检查。

队列是一种先进先出(First In First Out，FIFO)的数据结构，而栈是一种后进先出(Last In First Out，LIFO)的数据结构。

6.4 实现图

首先,需要使用代码来实现图。图由多个节点组成。每个节点都与邻近节点相连，散列表能够将键映射到值。在这里，你将要将节点映射到所有邻居。

表示这种映射的代码如下。

graph = {}
graph["you"] = ["alice","bob","claire"]

注意，“you” 被映射到了一个数组，因此graph["you"]是一个数组,其中包含了"you"的所有邻居。

6.5 实现算法

概述一下这种算法的工作原理

首先，创建一个队列。在Python中，可使用函数deque来创建一个双端队列。

from collections import deque
search_queue = deque() # 创建一个队列
search_queue += graph["you"] # 将你的邻居都加入到这个搜索队列中

别忘了，graph["you"]是一个数组，其中包含你的所有邻居，如["alice", "bob","claire"]。这些邻居都将加入到搜索队列中。

while search_queue: # 只要队列不为空
    person = search_queue.popleft() # 就取出其中地第一个人
    if person_is_seller(person): # 检查这个人是否是芒果经销商
        print person + "is a mango seller!" # 是芒果经销商
    else:
        search_queue += graph[person] # 不是芒果经销商.将这个人的朋友都加入搜索队列
return False # 如果达到了这里,就说明队列中没有人是芒果经销商

最后你还需编写函数person_is_seller,判断一个人是不是芒果经销商.

def person_is_seller(name):
    return name[-1] == 'm'

这个函数检查人的姓名是否以m结尾:如果是，他就是芒果销售商。这种判断方法有点搞笑，但就这个示例而言是可行的。下面来看看广度优先搜索的执行过程。

这个算法将不断执行,直到满足以下条件之一:

找到一位芒果经销商;
队列变成空的,这意味着你的人际关系中没有芒果经销商。

检查完一个人后，应将其标记为已检查，且不再检查他。如果不这样做，就可能会导致无限循环。

检查一个人之前，要确认之前没检查过他，这很重要。为此，你可使用一个列表来记录检查过的人。

考虑到这一点后，广度优先搜索的最终代码如下。

def search(name):
    search_queue = deque()
    search_queue += graph[name]
    searched = [] # 这个数组用于记录检查过的人
    while search_queue:
        person = search_queue.popleft()
        if person not in searched: # 仅当这个人没检查过时才检查
            if person_is_seller(person):
                print person + " is a mango seller!"
                return True
            else:
                search_queue += graph[person]
                searched.apppend(person) # 将这个人标记为检查过
    return False


search("you")

运行时间

如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行(记住，边是从一个人到另一个人的箭头或连接)，因此运行时间至少为O(边数)。

你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为 O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点(vertice)数，E为边数。

七、狄克斯特拉算法

广度优先算法，它找出的是段数最少的路径。如果要找出最快的路径可使用另一种算法——狄克斯特拉算法。

7.1 使用狄克斯特拉算法

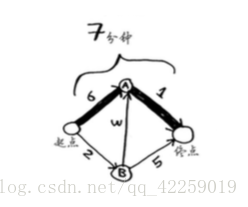
下面来看看如何对下面的图使用这种算法。

其中每个数字表示的都是时间，单位分钟。为找出从起点到终点耗时最短的路径，你将使用狄克斯特拉算法。

如果你使用广度优先搜索，将得到下面这条段数最少的路径。

这条路径耗时7分钟。下面来看看能否找到耗时更短的路径!狄克斯特拉算法包含4个步骤。

(1) 找出“最便宜”的节点，即可在最短时间内到达的节点。

(2) 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。

(3) 重复这个过程，直到对图中的每个节点都这样做了。

(4) 计算最终路径。

7.2 术语

狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重。

带权重的图称为加权图(weighted graph)，不带权重的图称为非加权图(unweighted graph)。

要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法。

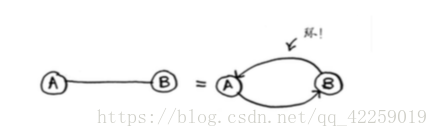
无向图意味着两个节点彼此指向对方，其实是一个环!

在无向图中，每条边都是一个环。狄克斯特拉算法只适用于有向无环图(directed acyclic graph，DAG)。

7.3 换钢琴

Rama，想拿一本乐谱换架钢琴。现在他需要确定的是，如何花最少的钱实现这个目标。我们来绘制一个图，列出大家的交换意愿。

这个图中的节点是大家愿意拿出来交换的东西，边的权重是交换时需要额外加多少钱。拿海报换吉他需要额外加30美元，拿黑胶唱片换吉他需要额外加15美元。Rama需要确定采用哪种路径将乐谱换成钢琴时需要支付的额外费用最少。为此，可以使用狄克斯特拉算法!

准备工作：创建一个表格，在其列出每个节点的开销。这里的开销指的是达到节点需要额外支付多少钱。

在执行狄克斯特拉算法的过程中，你将不断更新这个表。为计算最终路径，还需在这个表中添加表示父节点的列。

第一步：找出最便宜的节点。在这里，换海报最便宜，不需要支付额外的费用。

第二步：计算前往该节点的各个邻居的开销。

现在的表中包含低音吉他和架子鼓的开销。这些开销是用海报交换它们时需要支付的额外费用，因此父节点为海报。这意味着，要到达低音吉他，需要沿从海报出发的边前行，对架子鼓来说亦如此。

再次执行第一步:下一个最便宜的节点是黑胶唱片——需要额外支付5美元。

再次执行第二步:更新黑胶唱片的各个邻居的开销。

你更新了架子鼓和吉他的开销！因为“黑胶唱片”前往“架子鼓”和吉他的开销更低，因此你将这些乐器的父节点改为黑胶唱片。

下一个最便宜的是吉他，因此更新其邻居的开销。

你终于计算出了用吉他换钢琴的开销，于是你将其父节点设置为吉他。最后，对最后一个节点——架子鼓，做同样的处理。

如果用架子鼓换钢琴，Rama需要额外支付的费用更少。因此，采用最便宜的交换路径时， Rama需要额外支付35美元。

知道了最短路径的开销，通过沿父节点回溯来确定最终路径。

7.4 负权边

狄克斯特拉算法这样假设:对于处理过的海报节点，没有前往该节点的更短路径。这种假设仅在没有负权边时才成立。因此，不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中，要找出最短路径，可使用另一种算法——贝尔曼福德算法。

7.5 实现

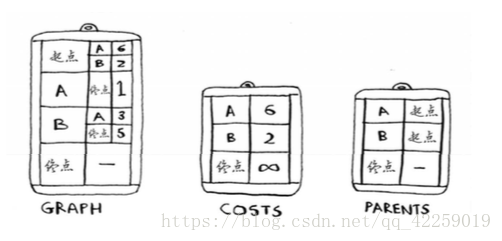
使用代码来实现狄克斯特拉算法，以下面的图为例。

解决这个问题的代码，需要三个散列表。

随着算法的进行，你将不断更新散列表costs和parents。


graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {} # 终点没有任何邻居

infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity

parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None

processed = []

node = find_lowest_cost_node(costs) # 在未处理的节点中找出开销最小的节点
while node is not None: # 这个while循环在所有节点都被处理过后结束
    cost = costs[node] 
    neighbors = graph[node] 
    for n in neighbors.keys(): # 遍历当前节点的所有邻居
        new_cost = cost + neighbors[n] 
        if costs[n] > new_cost: # 如果经当前节点前往该邻居更近，
            costs[n] = new_cost # 就更新该邻居的开销
            parents[n] = node   # 同时将该邻居的父节点设置为当前节点
    processed.append(node) # 将当前节点标记为处理过
    node = find_lowest_cost_node(costs) #

7.6 小结

广度优先搜索用于在非加权图中查找最短路径。
狄克斯特拉算法用于在加权图中查找最短路径。
仅当权重为正时狄克斯特拉算法才管用。
如果图中包含负权边，请使用贝尔曼-福德算法。

八、贪婪算法

8.1 教室调度问题

你希望在这间教室上尽可能多的课。如何选出尽可能多且时间不冲突的课程呢?

具体做法如下。

(1) 选出结束最早的课，它就是要在这间教室上的第一堂课。

(2) 接下来，必须选择第一堂课结束后才开始的课。同样，你选择结束最早的课，这将是要在这间教室上的第二堂课。

重复这样做就能找出答案!

贪婪算法很简单:每步都采取最优的做法。在这个示例中，你每次都选择结束最早的课。用专业术语说，就是你每步都选择局部最优解，最终得到的就是全局最优解。

8.2 背包问题

假设你是个贪婪的小偷，背着可装35磅(1磅≈0.45千克)重东西的背包，在商场伺机盗窃各种可装入背包的商品。你力图往背包中装入价值最高的商品，你会使用哪种算法呢?

同样，你采取贪婪策略，这非常简单。

(1) 盗窃可装入背包的最贵商品。

(2) 再盗窃还可装入背包的最贵商品，以此类推。

假设你的背包可装35磅的东西。音响最贵，你把它给偷了，但背包没有空间装其他东西了。你偷到了价值3000美元的东西。且慢!如果不是偷音响，而是偷笔记本电脑和吉他，总价将为3500美元!

从这个示例你得到了如下启示:在有些情况下，完美是优秀的敌人。有时候，你只需找到一个能够大致解决问题的算法，此时贪婪算法正好可派上用场，因为它们实现起来很容易，得到的结果又与正确结果相当接近。

8.3 集合覆盖问题

假设你办了个广播节目，要让全美50个州的听众都收听得到。为此，你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用，因此你力图在尽可能少的广播台播出。每个广播台都覆盖特定的区域，不同广播台的覆盖区域可能重叠。如何找出覆盖全美50个州的最小广播台集合呢?具体方法如下：

(1) 列出每个可能的广播台集合，这被称为幂集(power set)。可能的子集有2^n个。

(2) 在这些集合中，选出覆盖全美50个州的最小集合。

随着广播台的增多，需要的时间将激增。没有任何算法可以足够快地解决这个问题!怎么办呢?

近似算法

(1) 选出这样一个广播台，即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖的州，也没有关系。

(2) 重复第一步，直到覆盖了所有的州。

这是一种近似算法(approximation algorithm)。在获得精确解需要的时间太长时，可使用近似算法。判断近似算法优劣的标准如下:

速度有多快;
得到的近似解与最优解的接近程度。

# 首先，创建一个列表，其中包含要覆盖的州。
states_needed = set(["mt", "wa", "or", "id", "nv", "ut","ca", "az"])
# 还需要有可供选择的广播台清单，我选择使用散列表来表示它。
stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
# 使用一个集合来存储最终选择地广播台
final_stations = set()

# 计算答案
best_station = None
states_covered = set()
for station, states_for_station in stations.items():
covered = states_needed & states_for_station 
while states_needed:
best_station = None
states_covered = set()
for station, states in stations.items():
covered = states_needed & states
if len(covered) > len(states_covered):
          best_station = station
          states_covered = covered
states_needed -= states_covered
final_stations.add(best_station)

8.4 NP完全问题

旅行商问题

元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
涉及“所有组合”的问题通常是NP完全问题。
不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
如果问题涉及序列(如旅行商问题中的城市序列)且难以解决，它可能就是NP完全问题。
如果问题涉及集合(如广播台集合)且难以解决，它可能就是NP完全问题。
 如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。

8.5 小结

贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。
对于NP完全问题，还没有找到快速解决方案。
面临NP完全问题时，最佳的做法是使用近似算法。
贪婪算法易于实现、运行速度快，是不错的近似算法。

九、动态规划

如何找到最优解，答案就是动态规划！动态规划先解决子问题，再逐步解决大问题。

动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。
在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。
每种动态规划解决方案都涉及网格。
单元格中的值通常就是你要优化的值。在前面的背包问题中，单元格的值为商品的价值。
每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网格的坐标轴。

十、K最近邻算法

KNN用于分类和回归，需要考虑最近的邻居。
分类就是编组。
回归就是预测结果(如数字)。
特征抽取意味着将物品(如水果或用户)转换为一系列可比较的数字。
能否挑选合适的特征事关KNN算法的成败。

十一、接下来如何做

11.1 树

二叉查找树

对于其中的每个节点，左子节点的值都比它小，而右子节点的值都比它大。

假设你要查找Maggie。为此，你首先检查根节点。

Maggie排在David的后面，因此你往右边找。

Maggie排在Manning前面，因此你往左边找。

终于找到了Maggie!这几乎与二分查找一样!在二叉查找树中查找节点时，平均运行时间为 O(log n)，但在最糟的情况下所需时间为O(n);而在有序数组中查找时，即便是在最糟情况下所需的时间也只有O(log n)，因此你可能认为有序数组比二叉查找树更佳。然而，二叉查找树的插入和删除操作的速度要快得多。

那在什么情况下使用二叉查找树呢?B树是一种特殊的二叉树，数据库常用它来存储数据。

如果对数据库或高级数据结构感兴趣，请研究如下数据结构:B树，红黑树，堆，伸展树。

11.2 反向索引

搜索引擎的工作原理。假设你有三个网页，内容如下。

我们根据网页的内容创建一个散列表。

这个散列表的键为单词，值为包含指定单词的页面。现在假设有用户搜索hi，在这种情况下，搜索引擎需要检查哪些页面包含hi。搜索引擎发现页面A和B包含hi，因此将这些页面作为搜索结果呈现给用户。

这是一种很有用的数据结构:一个散列表，将单词映射到包含它的页面。这种数据结构被称为反向索引(inverted index)，常用于创建搜索引擎。如果你对搜索感兴趣，从反向索引着手研究是不错的选择。

11.3 傅里叶变换

给定一首歌曲，傅里叶变换能够将其中的各种频率分离出来。

如果能够将歌曲分解为不同的频率，就可强化你关心的部分，如强化低音并隐藏高音。傅里叶变换非常适合用于处理信号，可使用它来压缩音乐。为此，首先需要将音频文件分解为音符。傅里叶变换能够准确地指出各个音符对整个歌曲的贡献，让你能够将不重要的音符删除。这就是MP3格式的工作原理!

数字信号并非只有音乐一种类型。JPG也是一种压缩格式，也采用了刚才说的工作原理。傅里叶变换还被用来地震预测和DNA分析。

11.4 并行算法

来看一个简单的例子。在最佳情况下，排序算法的速度大致为O(n log n)。众所周知，对数组进行排序时，除非使用并行算法，否则运行时间不可能为O(n)!对数组进行排序时，快速排序的并行版本所需的时间为O(n)。

并行算法设计起来很难，要确保它们能够正确地工作并实现期望的速度提升也很难。有一点是确定的，那就是速度的提升并非线性的，因此即便你的笔记本电脑装备了两个而不是一个内核，算法的速度也不可能提高一倍，其中的原因有两个。

并行性管理开销。假设你要对一个包含1000个元素的数组进行排序，如何在两个内核之间分配这项任务呢?如果让每个内核对其中500个元素进行排序，再将两个排好序的数组合并成一个有序数组，那么合并也是需要时间的。
负载均衡。假设你需要完成10个任务，因此你给每个内核都分配5个任务。但分配给内核 A的任务都很容易，10秒钟就完成了，而分配给内核B的任务都很难，1分钟才完成。这意味着有那么50秒，内核B在忙死忙活，而内核A却闲得很!你如何均匀地分配工作，让两个内核都一样忙呢?

要改善性能和可扩展性，并行算法可能是不错的选择!

11.5 MapReduce

有一种特殊的并行算法正越来越流行，它就是分布式算法。在并行算法只需两到四个内核时，完全可以在笔记本电脑上运行它，但如果需要数百个内核呢?在这种情况下，可让算法在多台计算机上运行。MapReduce是一种流行的分布式算法，你可通过流行的开源工具Apache Hadoop来使用它。

11.5.1 分布式算法为何很有用

假设你有一个数据库表，包含数十亿乃至数万亿行，需要对其执行复杂的SQL查询。在这种情况下，你不能使用MySQL，因为数据表的行数超过数十亿后，它处理起来将很吃力。相反，你需要通过Hadoop来使用MapReduce!

又假设你需要处理一个很长的清单，其中包含100万个职位，而每个职位处理起来需要10秒。如果使用一台计算机来处理，将耗时数月!如果使用100台计算机来处理，可能几天就能完工。

分布式算法非常适合用于在短时间内完成海量工作，其中的MapReduce基于两个简单的理念:映射(map)函数和归并(reduce)函数。

11.5.2 映射函数

你有一个URL清单，需要下载每个URL指向的页面并将这些内容存储在数组 arr2中。对于每个URL，处理起来都可能需要几秒钟。如果总共有1000个URL，可能耗时几小时!

如果有100台计算机，而map能够自动将工作分配给这些计算机去完成就好了。这样就可同时下载100个页面，下载速度将快得多!这就是MapReduce中“映射”部分基于的理念。

11.5.3 归并函数

归并函数可能令人迷惑，其理念是将很多项归并为一项。映射是将一个数组转换为另一个数组。而归并是将一个数组转换为一个元素。

MapReduce使用这两个简单概念在多台计算机上执行数据查询。数据集很大，包含数十亿行时，使用MapReduce只需几分钟就可获得查询结果，而传统数据库可能要耗费数小时。

11.6 布隆过滤器和HyperLogLog

假设你管理着网站Reddit。每当有人发布链接时，你都要检查它以前是否发布过，因为之前未发布过的故事更有价值。

又假设你在Google负责搜集网页，但只想搜集新出现的网页，因此需要判断网页是否搜集过。

再假设你管理着提供网址缩短服务的bit.ly，要避免将用户重定向到恶意网站。你有一个清单，其中记录了恶意网站的URL。你需要确定要将用户重定向到的URL是否在这个清单中。

这些都是同一种类型的问题，涉及庞大的集合。

给定一个元素，你需要判断它是否包含在这个集合中。为快速做出这种判断，可使用散列表。例如，Google可能有一个庞大的散列表，其中的键是已搜集的网页。

要判断是否已搜集adit.io，可在这个散列表中查找它。

adit.io是这个散列表中的一个键，这说明已搜集它。散列表的平均查找时间为O(1)，即查 8 找时间是固定的，非常好!

只是Google需要建立数万亿个网页的索引，因此这个散列表非常大，需要占用大量的存储空间。Reddit和bit.ly也面临着这样的问题。面临海量数据，你需要创造性的解决方案!

11.6.1 布隆过滤器

布隆过滤器提供了解决之道。布隆过滤器是一种概率型数据结构，它提供的答案有可能不对，但很可能是正确的。为判断网页以前是否已搜集，可不使用散列表，而使用布隆过滤器。使用散列表时，答案绝对可靠，而使用布隆过滤器时，答案却是很可能是正确的。

可能出现错报的情况，即Google可能指出“这个网站已搜集”，但实际上并没有搜集。
不可能出现漏报的情况，即如果布隆过滤器说“这个网站未搜集”，就肯定未搜集。

布隆过滤器的优点在于占用的存储空间很少。使用散列表时，必须存储Google搜集过的所有 URL，但使用布隆过滤器时不用这样做。布隆过滤器非常适合用于不要求答案绝对准确的情况，前面所有的示例都是这样的。对bit.ly而言，这样说完全可行:“我们认为这个网站可能是恶意的，请倍加小心。”

11.6.2 HyperLogLog

HyperLogLog是一种类似于布隆过滤器的算法。如果Google要计算用户执行的不同搜索的数量，或者Amazon要计算当天用户浏览的不同商品的数量，要回答这些问题，需要耗用大量的空间!对Google来说，必须有一个日志，其中包含用户执行的不同搜索。有用户执行搜索时，Google 必须判断该搜索是否包含在日志中:如果答案是否定的，就必须将其加入到日志中。即便只记录一天的搜索，这种日志也大得不得了!

HyperLogLog近似地计算集合中不同的元素数，与布隆过滤器一样，它不能给出准确的答案，但也八九不离十，而占用的内存空间却少得多。

面临海量数据且只要求答案八九不离十时，可考虑使用概率型算法!

11.7 SHA 算法

假设你有一个键，需要将其相关联的值放到数组中。你使用散列函数来确定应将这个值放在数组的什么地方。

这样查找时间是固定的。当你想要知道指定键对应的值时，可再次执行散列函数，它将告诉

你这个值存储在什么地方，需要的时间为O(1)。在这个示例中，你希望散列函数的结果是均匀分布的。散列函数接受一个字符串，并返回一个索引号。

11.7.1 比较文件
另一种散列函数是安全散列算法(secure hash algorithm，SHA)函数。给定一个字符串，SHA返回其散列值。

SHA是一个散列函数，它生成一个散列值——一个较短的字符串。用于创建散列表的散列函数根据字符串生成数组索引，而SHA根据字符串生成另一个字符串。

对于每个不同的字符串，SHA生成的散列值都不同。

你可使用SHA来判断两个文件是否相同，这在比较超大型文件时很有用。假设你有一个4 GB 的文件，并要检查朋友是否也有这个大型文件。为此，你不用通过电子邮件将这个大型文件发送给朋友，而可计算它们的SHA散列值，再对结果进行比较。 8

11.7.2 检查密码

SHA还让你能在不知道原始字符串的情况下对其进行比较。例如，假设Gmail遭到攻击，攻击者窃取了所有的密码!你的密码暴露了吗?没有，因为Google存储的并非密码，而是密码的 SHA散列值!你输入密码时，Google计算其散列值，并将结果同其数据库中的散列值进行比较。

Google只是比较散列值，因此不必存储你的密码!SHA被广泛用于计算密码的散列值。这种散列算法是单向的。你可根据字符串计算出散列值。但你无法根据散列值推断出原始字符串。

这意味着计算攻击者窃取了Gmail的SHA散列值，也无法据此推断出原始密码!你可将密码转换为散列值，但反过来不行。

SHA实际上是一系列算法:SHA-0、SHA-1、SHA-2和SHA-3。SHA-0和SHA-1 已被发现存在一些缺陷。如果你要使用SHA算法来计算密码的散列值，请使用SHA-2或SHA-3。当前，最安全的密码散列函数是bcrypt，但没有任何东西是万无一失的。

11.8 局部敏感的散列算法

SHA还有一个重要特征，那就是局部不敏感的。假设你有一个字符串，并计算了其散列值。如果你修改其中的一个字符，再计算其散列值，结果将截然不同!这很好，让攻击者无法通过比较散列值是否类似来破解密码。

有时候，你希望结果相反，即希望散列函数是局部敏感的。在这种情况下，可使用Simhash。如果你对字符串做细微的修改，Simhash生成的散列值也只存在细微的差别。这让你能够通过比较散列值来判断两个字符串的相似程度，这很有用!

Google使用Simhash来判断网页是否已搜集。
老师可以使用Simhash来判断学生的论文是否是从网上抄的。
Scribd允许用户上传文档或图书，以便与人分享，但不希望用户上传有版权的内容!这个网站可使用Simhash来检查上传的内容是否与小说《哈利·波特》类似，如果类似，就自动拒绝。

需要检查两项内容的相似程度时，Simhash很有用。

11.9 Diffie-Hellman 密钥交换

它以优雅的方式解决了一个古老的问题:如何对消息进行加密，以便只有收件人才能看懂呢?

最简单的方式是设计一种加密算法，如将a转换为1，b转换为2，以此类推。这样，如果我给你发送消息“4,15,7”，你就可将其转换为“d,o,g”。但我们必须就加密算法达成一致，这种方式才可行。我们不能通过电子邮件来协商，因为可能有人拦截电子邮件，获悉加密算法，进而破译消息。即便通过会面来协商，这种加密算法也可能被猜出来——它并不复杂。因此，我们每天都得修改加密算法，但这样我们每天都得会面!

即便我们能够每天修改，像这样简单的加密算法也很容易使用蛮力攻击破解。假设我看到消息“9,6,13,13,16 24,16,19,13,5”，如果使用加密算法a = 1、b = 2等，转换结果将如下。

结果是一堆乱码。我们来尝试加密算法a = 2、b = 3等。

结果对了!像这样的简单加密算法很容易破解。在二战期间，德国人使用的加密算法比这复杂得多，但还是被破解了。Diffie-Hellman算法解决了如下两个问题。

双方无需知道加密算法。他们不必会面协商要使用的加密算法。
要破解加密的消息比登天还难。

Diffie-Hellman使用两个密钥:公钥和私钥。顾名思义，公钥就是公开的，可将其发布到网站上，通过电子邮件发送给朋友，或使用其他任何方式来发布。你不必将它藏着掖着。有人要向你发送消息时，他使用公钥对其进行加密。加密后的消息只有使用私钥才能解密。只要只有你知道私钥，就只有你才能解密消息!

Diffie-Hellman算法及其替代者RSA依然被广泛使用。如果你对加密感兴趣，先着手研究 Diffie-Hellman算法是不错的选择:它既优雅又不难理解。

11.10 线性规划

最好的东西留到最后介绍。线性规划是我知道的最酷的算法之一。

线性规划用于在给定约束条件下最大限度地改善指定的指标。例如，假设你所在的公司生产两种产品:衬衫和手提袋。衬衫每件利润2美元，需要消耗1米布料和5粒扣子;手提袋每个利润3 美元，需要消耗2米布料和2粒扣子。你有11米布料和20粒扣子，为最大限度地提高利润，该生产多少件衬衫、多少个手提袋呢?

在这个例子中，目标是利润最大化，而约束条件是拥有的原材料数量。

再举一个例子。你是个政客，要尽可能多地获得支持票。你经过研究发现，平均而言，对于每张支持票，在旧金山需要付出1小时的劳动(宣传、研究等)和2美元的开销，而在芝加哥需要付出1.5小时的劳动和1美元的开销。在旧金山和芝加哥，你至少需要分别获得500和300张支持票。你有50天的时间，总预算为1500美元。请问你最多可从这两个地方获得多少支持票?

这里的目标是支持票数最大化，而约束条件是时间和预算。

你可能在想，本书花了很大的篇幅讨论最优化，这与线性规划有何关系?所有的图算法都可使用线性规划来实现。线性规划是一个宽泛得多的框架，图问题只是其中的一个子集。但愿你听到这一点后心潮澎湃!

线性规划使用Simplex算法，这个算法很复杂，