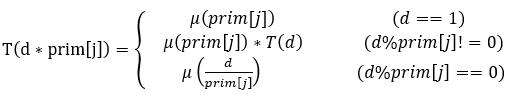HDU 5663 Hillan and the girl（莫比乌斯反演+分块求和）

大致题意：给你两个数字n和m，让你求 $\sum_{i=1}^{n}\sum_{j=1}^{m}f(i,j)$ ，其中f(i,j)表示gcd(i,j)是否为完全平方数，如果是则f(i,j)==0，否则为f(i,j)==1。

首先，有了之前 BZOJ 2301 的经验，这道题目可以比较简单的讲。BZOJ 2301 这题是求一定范围内的两个数字gcd为1的组数。这题我直接在那个的基础上面讲。

根据之前莫比乌斯反演的结果：

$\large F(i)=\sum_{i|d}f(d)=>f(i)=\sum_{i|d}\mu(\frac{d}{i})F(d)=\sum_{i|d}\mu(\frac{d}{i})\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor$

到这道题的话，最后结果就是： $\large ans=n*m-\sum_{x^2}^{min(n,m)}\sum_{x^2|d}^{min(n,m)}\mu(\frac{d}{x^2})*\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor$

考虑交换求和次序： $\large ans=n*m-\sum_{d=1}^{min(n,m)}\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor*\sum_{x^2|d}^{min(n,m)}\mu(\frac{d}{x^2})$

到目前为止，我们这个式子即使用上分块求和优化，它的的复杂度是 $O(TN\sqrt{N})$ 的，注意到本题N可以到1e7这大，然后T也有1e4这么多组，因此到这一步是远远不够的。对于右边这个求和式子，我们考虑它的性质。我们不妨令 $T(d)=\sum_{x^2|d}\mu(\frac{d}{x^2})$ 。分情况考虑：

当d为质数的时候，要满足x^2|d只有当x为1的时候，因此此时T(d)= $\mu$ (d)。

当d%p!=0的时候，这个p表示某一个质数。此时我们可以考虑利用莫比乌斯函数的积性：

$\large T(d*p)=\sum_{x^2|d}\mu(\frac{d*p}{x^2})=\mu(p)*\sum_{x^2|d}\mu(\frac{d}{x^2})=\mu(p)*T(d)$

当d%p==0的时候。表明d已经可以被p分解，那么d*p一定可以被p分解两次以上，因此T(d*p)的x的取值会比T(d)多一个p*p，那么有： $T(d*p)=\mu(\frac{d*p}{p*p})+\sum_{x^2|d}\mu(\frac{d*p}{x^2})$ ，注意到右边的和式的x取值不会到p，那么意味着 $\frac{d*p}{x^2}$ 也能被p分解两次，即对应分解质因数p的指数大于1。根据莫比乌斯函数的定义，只要 $\mu$ (x)种出现一个质因子的指数大于1，那么 $\mu$ (x)=0。因此右边那一项等于0。

由此我么们可以写出T(d)的表达式：

经过整理，我们发现，T本身就可以看作莫比乌斯函数的变种，因此我可以直接用T自己的表达式：

$\large T(d*p)\begin{cases}T(p) & d = 1 \\ T(p)*T(j) & d\%p!=0 \\ T(\frac{d}{p}) & d\%p==0 \end{cases}$

这样我们就可以在预处理的时候，仿照线性筛素数和莫比乌斯函数的方法，O(N)的求出T(d)。然后再对这个T(d)进行求和，仿照BZOJ 2301 的方法进行分块求和优化，这样询问一次的复杂度就是 $\large O(\sqrt{N})$ 。总的时间复杂度就是 $\large O(T\sqrt{N})$ 。具体见代码：

#include<bits/stdc++.h>
#define IO ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define LL long long
#define N 10000010

using namespace std;
 
int s[N],p[N],T[N];
bool isp[N];
 
void init()
{
    int sz=0;
    s[1]=T[1]=1; 
    for(int i=2;i<N;i++)
    {
        if(!isp[i]) p[++sz]=i,T[i]=-1;
        for(int j=1;j<=sz&&i*p[j]<N;j++)
        {
            isp[i*p[j]]=1;
            if(i%p[j]==0)
            {
                T[p[j]*i]=T[i/p[j]];
                break;
            } else T[p[j]*i]=-T[i];
        }
        s[i]=s[i-1]+T[i];
    }
}
 
LL cal(int n,int m)
{
    LL res=0,last;
    for(int i=1;i<=n&&i<=m;i=last+1)
    {
        last=min(n/(n/i),m/(m/i));
        res+=1LL*(s[last]-s[i-1])*(n/i)*(m/i);
    }
    return res;
}
 
int main()
{
    int b,d,n;
    IO; init(); cin>>n;
    while(n--)
    {
        cin>>b>>d;
        cout<<(LL)b*d-cal(b,d)<<endl;
    }
    return 0;
}

HDU 5663 Hillan and the girl（莫比乌斯反演+分块求和）

猜你喜欢